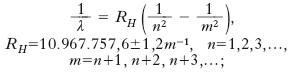spettroscopia

spettroscopia Settore della scienza che ha per oggetto lo studio degli spettri delle radiazioni elettromagnetiche e corpuscolari. Anche, più specificatamente, il metodo relativo alla produzione e all’analisi di tali spettri.

Caratteri generali

In relazione alla natura delle radiazioni, si parla di s. ottica o nel visibile, di s. X, di s. β, di s. neutronica ecc. Per estensione, si parla anche di s. elastica, e in particolare di s. acustica, se si ha a che fare con onde elastiche e in particolare con onde sonore. Tutte queste specie di s. si rifanno, direttamente, oppure per estensione analogica, ai procedimenti e al linguaggio della s. ottica, la prima a essere attuata; ciò è particolarmente vero per i vari settori spettroscopici relativi al campo delle radiazioni elettromagnetiche che va dalle radioonde ai raggi X, tanto che nella s. ottica si finisce con il comprendere spesso tutti i settori nominati, che interessano cioè l’insieme delle radiazioni la cui emissione e il cui assorbimento dipendono da proprietà atomiche e molecolari: per tale motivo la s. ottica costituisce uno dei capitoli più importanti della fisica atomica e molecolare, in cui con mezzi sperimentali piuttosto semplici si riesce a penetrare nell’intima struttura della materia.

Accanto alla s. d’emissione, che si occupa degli spettri ottenuti analizzando la radiazione emessa da una sorgente, si considera anche la s. d’assorbimento, che si occupa degli spettri ottenuti facendo passare un fascio di radiazioni note attraverso una sostanza (spettri d’assorbimento); la distinzione fra questi due tipi di s. è relativa al diverso modo sperimentale di procedere, perché spettri di emissione e spettri di assorbimento si equivalgono quanto alle informazioni da essi deducibili. Nella s. di diffusione, il campione viene illuminato con una radiazione di data frequenza e viene misurata la radiazione diffusa in opportune direzioni sia alla stessa frequenza (diffusione Rayleigh) sia a frequenze diverse (diffusione Raman).

La s. può essere suddivisa in s. atomica, molecolare, nucleare, che studiano gli spettri originati da transizioni aventi luogo rispettivamente tra livelli energetici atomici, molecolari, nucleari; per estens., si parla anche di s. adronica (o subnucleare) per indicare lo studio degli spettri di massa delle particelle (adroni) che danno luogo a interazioni forti.

Cenni storici

La s. prende le mosse dagli studi di I. Newton, il quale nel 1665 interpretò lo sparpagliamento operato da un prisma di vetro di un sottile fascetto di luce solare in un ventaglio di raggi colorati (che su uno schermo bianco produce una banda luminosa variamente colorata, lo spettro della luce solare) come la decomposizione della luce bianca nei vari colori che la compongono, deflessi in maniera diversa dal prisma. Il primo spettro ‘artificiale’ fu osservato nel 1752 da T. Melville, che esaminò varie fiamme colorate attraverso un prisma, limitando la porzione visibile della sorgente con l’aiuto di uno schermo forato; in questo modo notò uno splendore straordinario nella regione gialla dello spettro prodotto dalla fiamma dell’alcol addizionato con cloruro di sodio o con salnitro, che attribuì alla predominanza di una radiazione monocromatica. Nel 1800 F.W. Herschel scoprì lo spettro infrarosso proiettando sul bulbo di un termometro lo spettro solare e osservando un aumento di temperatura variabile con le diverse regioni dello spettro, che si verifica anche al di là del rosso, in una regione dove non si hanno radiazioni visibili. A questa scoperta ne fece immediatamente seguito un’altra, da parte di J.W. Ritter, inerente radiazioni invisibili all’altra estremità dello spettro solare, di là del violetto, che danno luogo alla riduzione dei sali d’argento. Nel 1814 numerose (576) righe oscure nello spettro visibile solare vennero scoperte da J. Fraunhofer, che collimò la luce solare con una stretta fenditura parallela agli spigoli del prisma e osservò in uscita dal prisma stesso lo spettro con un cannocchiale; in tal modo Fraunhofer riuscì a risolvere per la prima volta la doppia riga oscura D (che in seguito risulterà coincidere con il doppietto giallo del sodio); accertò inoltre che la luce delle stelle presenta uno spettro con righe oscure differenti da quelle solari, concludendo che la causa di queste righe oscure non è da attribuire all’aria atmosferica attraversata dalla luce. Fraunhofer studiò anche lo spettro della parte inferiore della fiamma di una candela, corrispondente allo spettro del carbonio, che costituì così il primo spettro di non metallo osservato, e dopo breve tempo descrisse gli spettri delle fiamme di alcuni idrocarburi e dell’arco voltaico nell’aria, osservato poco prima anche da W.H. Wollaston. Nel 1832 D. Brewster scoprì gli spettri di assorbimento e nel 1833 W.H. Miller studiò lo spettro di assorbimento dei vapori dello iodio e del bromo. Nel 1856 J.W. Swan studiò gli spettri delle fiamme dei composti idrogenati del carbonio e segnalò che un preparato contenente una parte su 250.000 di sodio dà una riga gialla chiaramente visibile. Sulla base di questa esperienza, giustificò la presenza di questa riga in quasi tutti gli spettri tramite le piccolissime quantità di sale marino presenti nell’atmosfera. Nel 1859 G.R. Kirchhoff dimostrò che il doppietto giallo caratteristico del sodio coincide con la doppia riga oscura D dello spettro solare ed enunciò la legge secondo cui una fiamma assorbe i ‘raggi’ che essa stessa emette; attribuì quindi le righe oscure dello spettro solare alla presenza nell’atmosfera del Sole di sostanze che possono comunicare a una fiamma la proprietà di emettere le righe luminose corrispondenti. Ad analoghe conclusioni era già giunto del tutto indipendentemente nel 1849 L. Foucault.

Nel 1860 Kirchhoff e R.W. Bunsen pubblicarono una prima memoria sull’analisi chimica fondata sull’osservazione dello spettro delle fiamme. Questa memoria segna la nascita della moderna s.: l’accertamento che ogni sostanza ha un suo caratteristico spettro d’emissione e d’assorbimento diede vita all’analisi spettroscopica, che divenne ben presto uno dei più efficaci strumenti di indagine chimica e fisica. Particolare importanza ha lo studio che è stato fatto dello spettro di emissione dell’elemento più semplice, l’idrogeno. Già nel 1885 J.J. Balmer scoprì che era possibile rappresentare analiticamente la successione delle righe allora note, nel visibile, mediante la relazione 1/λ=a/4−a/m2, ove λ è la lunghezza d’onda (nel vuoto), a è una costante e m=3, 4, 5, ... Successivamente (1890) J.R. Rydberg mostrò che la serie spettrale di Balmer nel visibile e altre serie di righe dell’idrogeno nell’ultravioletto e nell’infrarosso potevano essere rappresentate mediante la relazione generale (equazione di Rydberg)

RH ha il nome di costante di Rydberg (per l’idrogeno); taluno dà il nome di costante di Rydberg alla quantità RHc, con c velocità della luce nel vuoto, che rappresenta la frequenza, circa 3,29∙1015 Hz, corrispondente alla radiazione avente numero di onde RH. Dando a n il valore 1, e quindi a m i successivi valori 2, 3, ..., si ottengono le lunghezze d’onda (precisamente, i loro inversi, cioè i numeri di onde) delle righe della serie di Lyman (1906), che si trova nell’ultravioletto all’incirca fra 912 e 1216 Å. Dando a n il valore 2 e quindi a m i valori 3, 4, ... si ottiene la già ricordata serie di Balmer (1885), che si trova nel visibile all’incirca fra 3648 e 6563 Å. Per valori maggiori di n, si hanno serie nell’infrarosso: la serie di Paschen (1922), per n=3, estesa all’incirca fra 0,8 e 1,8 μm; la serie di Brackett, per n=4, all’incirca fra 1,5 e 4 μm; la serie di Pfund (1924), per n=5, all’incirca fra 2,2 e 7,4 μm e così via. Come mostra l’equazione di Rydberg, i singoli numeri di onde possono essere interpretati come differenze fra un termine spettrale fisso, o testa della serie, che, per es., vale RH/4 per la serie di Balmer, e termini spettrali correnti che, nel caso della serie di Balmer, sono RH/9, RH/16, ...; tale circostanza costituisce il cosiddetto principio di combinazione, enunciato (1908) da W. Ritz. In base a tale principio è facile vedere che la somma o la differenza dei numeri di onde di due righe può dare il numero di onde di una terza riga.

L’equazione di Rydberg si applica abbastanza bene anche a sistemi idrogenoidi, cioè ad atomi ionizzati sino ad avere un solo elettrone (He+, Li++ ecc.), salvo il fatto che la costante di Rydberg varia leggermente, aumentando con il numero di massa (esprimendola in m−1, aumenta al valore 10.973.731, cioè solo dello 0,06%, passando dall’idrogeno a un elemento, ipotetico, di massa atomica infinitamente grande); non è così invece per atomi neutri, diversi da quello dell’idrogeno: per dar conto dei risultati sperimentali, i termini spettrali devono avere la forma R/(N−α)2, dove R è la costante di Rydberg appropriata all’elemento in esame, N è un intero e α, che è una quantità minore di 1, ha il nome di correzione di Rydberg per l’elemento e per la serie spettrale considerati. Così, dallo stesso Rydberg fu proposta (1900) la seguente equazione:

in cui n e m sono interi caratteristici rispettivamente della serie e della riga, come nell’equazione di Rydberg, mentre α e β sono le correzioni.

I dati spettroscopici (e la loro classificazione mediante formule empiriche) hanno costituito la base sperimentale della fisica atomica e hanno contribuito alla nascita della fisica quantistica.

S. atomica

Linee generali. Gli atomi liberi di ciascun elemento allo stato di gas rarefatto emettono e assorbono radiazione elettromagnetica, in particolare luce, solo in corrispondenza di certi valori ben definiti della frequenza tipici dell’elemento. La generica capacità degli atomi di emettere o assorbire radiazione elettromagnetica è dovuta alla presenza al loro interno di particelle elettricamente cariche, in particolare degli elettroni legati al nucleo da forze elettriche. L’interpretazione degli spettri atomici è immediata in termini di livelli energetici e di transizioni tra di essi: a ciascun atomo è associato un insieme discreto di stati stazionari con ben determinati valori dell’energia o livelli energetici; l’emissione o l’assorbimento della radiazione di una determinata frequenza (riga spettrale) è dovuta alla transizione tra due stati stazionari causata dalla perturbazione dovuta all’interazione col campo elettromagnetico.

I livelli energetici dell’atomo hanno trovato una prima sistemazione nel modello atomico di N. Bohr (➔ atomo) e una coerente spiegazione nella meccanica (➔) quantistica. L’esistenza dei livelli energetici è stata originariamente suggerita proprio dalle notevoli regolarità osservate fenomenologicamente negli spettri atomici, come quella compendiata nel principio di combinazione di Ritz, che hanno portato a far corrispondere a ogni termine spettrale una coppia di livelli energetici dell’atomo. Infatti, se si associano alla radiazione di frequenza ν fotoni di energia hν (con h costante di Planck), per la conservazione dell’energia alla transizione tra due stati stazionari ai quali rispettivamente compete l’energia Ei ed Ef è associata l’emissione o l’assorbimento di un fotone, di modo che Ef−Ei=hν e quindi ν=c/λ=(Ef−Ei)/h. Pertanto a ogni termine spettrale corrisponde una coppia di livelli energetici; non è vero il contrario, a causa delle regole di selezione.

fig. 1

L’intensità di una riga dello spettro di emissione o di assorbimento è proporzionale al numero di fotoni emessi o assorbiti nell’unità di tempo e quindi al numero di atomi presenti nello stato iniziale della transizione e alla probabilità che questa abbia luogo nell’unità di tempo. Se sono noti i termini spettrali e i corrispondenti livelli energetici, è possibile costruire uno schema come quello riportato in fig. 1 (le linee orizzontali indicano i livelli, le frecce verticali le transizioni; all’assorbimento è associata una freccia verso l’alto, all’emissione verso il basso; la lunghezza della freccia è proporzionale alla frequenza della riga). Il numero di transizioni che si hanno tra N livelli è pari (se non intervengono regole di selezione) al numero di coppie di livelli N(N−1)/2. In realtà le righe spettrali (sia in emissione sia in assorbimento) hanno larghezza finita, cioè l’intensità della radiazione è diversa da zero in un intervallo molto piccolo della frequenza. La larghezza intrinseca o naturale di una riga (➔ monocromatico) è legata all’indeterminazione ΔE dell’energia degli stati eccitati dell’atomo, i quali avendo una vita media τ (dell’ordine di 10−8 s, molto maggiore del periodo, ∿10−14s, delle radiazioni coinvolte), per il principio di indeterminazione hanno necessariamente ΔE=h/τ. L’andamento dell’intensità in funzione della frequenza per una riga centrata intorno a νo è dato da:

con Γ larghezza a metà altezza della riga, pari a 1/τ per una transizione che coinvolga il livello fondamentale.

fig. 2

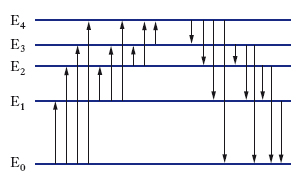
Per poter descrivere e interpretare gli spettri atomici è necessario considerare non solo i valori dell’energia che competono ai vari stati in cui può trovarsi l’atomo, ma anche quelli del momento angolare. La conservazione del momento angolare proibisce infatti alcune transizioni o, come si dice, impone regole di selezione. Se si indica con J il momento angolare totale (somma dei momenti angolari orbitali e degli spin) degli elettroni di un atomo e con J il corrispondente numero quantico [∣J∣2=J (J+1)ℏ2], le transizioni di dipolo elettrico permesse, nelle quali il fotone che ha spin 1 è emesso con momento angolare orbitale nullo, sono solo quelle che comportano variazioni di J pari a 0 oppure a ±1. Per alcuni atomi (idrogeno e metalli alcalini) sussiste una ulteriore semplice regola di selezione, in base alla quale il momento angolare orbitale L degli elettroni deve variare nelle transizioni di dipolo elettrico di un’unità. Tenendo conto dei numeri quantici di momento angolare J e L, i livelli energetici di un atomo possono essere organizzati come in fig. 2 (schema di Grotrian).

Gli stati con momento angolare orbitale L=0, 1, 2, 3, 4, ... sono solitamente contrassegnati rispettivamente con le lettere S, P, D, F, G, ...; il pedice alla destra di questa lettera indica il valore del momento angolare totale J. Per comodità di disegno, in fig. 2 sono stati riportati nella colonna relativa a L=3 stati con lo stesso valore di L ma con diverso valore di J. Ogni stato è anche caratterizzato con un numero intero (1S, 2S, 2P, 3S, 3P ecc.) che fornisce l’ordine progressivo del livello nella scala delle energie (questo numero intero coincide generalmente con il numero quantico principale). L’energia zero può essere attribuita allo stato fondamentale dell’atomo neutro (l’energia degli altri livelli risulta allora positiva) oppure allo stato fondamentale dell’atomo ionizzato (in tal caso l’energia dei livelli dell’atomo neutro risulta negativa). In uno schema di Grotrian la regola di selezione relativa alle variazioni del momento angolare orbitale L si traduce nel fatto che sono permesse transizioni di dipolo elettrico solo tra colonne contigue. Le linee inclinate in fig. 2 indicano tali transizioni, i numeri riportati in queste linee sono le lunghezze d’onda della radiazione (emessa o assorbita) in nm. Poiché la tipica separazione tra i livelli energetici dell’atomo corrispondenti all’eccitazione degli elettroni più esterni è dell’ordine dell’elettronvolt, gli spettri atomici cadono nel campo dell’infrarosso vicino, del visibile e dell’ultravioletto vicino; infatti, la frequenza della radiazione relativa a una transizione tra due livelli con Ef−Ei∿1eV è ν=(Ef−Ei)/h∿3∙1014∙s−1 e la sua lunghezza d’onda è λ=c/ν∿10−6m.

Molto spesso le righe di uno spettro atomico sono multiple, cioè migliorando il potere risolutivo dello spettroscopio si presentano come un gruppo (multipletto) di due o più righe molto vicine (doppietto, tripletto ecc.), mostrando una struttura fine o una struttura iperfine che presuppone una molteplicità dei livelli atomici. La molteplicità che dà luogo alla struttura fine è dovuta al fatto che ciascun elettrone atomico, dotato di momento (di dipolo) magnetico intrinseco μ, è immerso nel campo magnetico H dovuto al suo movimento e a quello degli altri elettroni: a seconda che il momento magnetico di ciascun elettrone sia parallelo o antiparallelo al campo magnetico, all’energia di un livello bisogna sottrarre o sommare un’energia potenziale magnetica μH e quindi ogni livello si scinderà in due o più livelli, a seconda delle orientazioni degli elettroni rispetto al campo. Le transizioni tra stati dello stesso multipletto generalmente cadono nel campo delle microonde. La struttura iperfine è dovuta all’interazione dei momenti magnetici degli elettroni con quello del nucleo. Una struttura fine può essere indotta artificialmente per effetto Zeeman sottoponendo il campione del quale si osserva lo spettro a un intenso campo magnetico (➔ Zeeman, Pieter) o per effetto Stark mediante un intenso campo elettrico (➔ Stark, Johannes). Concludendo, la rilevazione degli spettri atomici è di fondamentale importanza perché consente di risalire ai livelli energetici che sono una fonte di informazione diretta sulla dinamica interna dell’atomo.

S. di assorbimento. La s. atomica di assorbimento (o in assorbimento) studia lo spettro della radiazione elettromagnetica che, emessa da opportuna sorgente, attraversa un campione costituito da atomi allo stato gassoso, prodotti mediante vaporizzazione e dissociazione del campione. L’intensità della radiazione rilevata in uscita dal campione (radiazione trasmessa) risulta più o meno attenuata rispetto a quella della radiazione incidente, in corrispondenza di determinati intervalli di frequenza comprendenti le frequenze di risonanza degli atomi in esame. Gli atomi che assorbono i fotoni incidenti vengono promossi in stati energetici superiori dai quali, dopo tempi assai brevi (dell’ordine dei 10−8s), tornano nel livello inferiore, riemettendo un fotone della stessa energia. Poiché i fotoni vengono riemessi in tutte le direzioni dello spazio, l’intensità della radiazione misurata lungo la direzione del raggio incidente risulta diminuita. Il principio che sottostà all’assorbimento della radiazione è lo stesso per campioni costituiti da atomi o da molecole. Mentre, però, le molecole sono caratterizzate anche da moti rotazionali e vibrazionali, e dai corrispondenti livelli energetici, negli atomi i soli livelli energetici coinvolti sono quelli elettronici, per cui le radiazioni in gioco appartengono alla regione dei raggi X (lunghezza d’onda λ pari a 10-10−2 nm) se sono eccitati elettroni dei gusci interni, al campo ottico (infrarosso, visibile, ultravioletto, complessivamente λ=1 mm-10 nm) se le transizioni riguardano elettroni appartenenti a orbitali di valenza.

Tipicamente, la s. di assorbimento atomico convenzionale riguarda radiazioni di lunghezza tra 200 e 900 nm, comprendenti cioè tutto il visibile e le regioni vicine dell’IR e dell’UV. Le righe di assorbimento comprese in tale intervallo corrispondono a transizioni che partono dallo stato fondamentale; a causa dell’elevato salto energetico che intercorre tra questo stato ed il primo eccitato, anche a temperature relativamente elevate più del 90% degli atomi si trovano nel livello elettronico di minore energia. La s. di assorbimento atomico è particolarmente utile in chimica nell’analisi elementare quantitativa, mentre per le applicazioni qualitative è preferibile la s. di emissione, che permette di rilevare più facilmente la presenza di elementi in tracce. La misura dell’attenuazione dell’intensità della radiazione per particolari frequenze permette di risalire alla concentrazione delle specie atomiche presenti, mediante la relazione di Lambert-Beer.

S. di emissione. La s. atomica di emissione (o in emissione) si basa sullo studio dello spettro della radiazione che viene emessa da un campione costituito da atomi isolati (e dunque allo stato di gas o vapore), quando essi vengono eccitati in stati elettronici superiori a quello fondamentale. Essendo questi stati non stabili, gli atomi tendono spontaneamente a tornare nel loro stato a minore energia e nel far ciò cedono l’eccesso di energia emettendo fotoni. Le frequenze emesse dipendono dal tipo di livelli elettronici coinvolti, come per l’assorbimento atomico, rispetto al quale l’emissione è per molti aspetti complementare.

La fonte di eccitazione può essere a sua volta una radiazione (e in particolare un laser, nel qual caso è possibile eccitare l’atomo selettivamente in un particolare stato elettronico) oppure una sorgente termica o elettrica, quale una fiamma, un arco elettrico, una scintilla. Queste ultime sorgenti sono quelle convenzionali, cui si fa in genere riferimento quando si parla di emissione atomica. Quando la sorgente è una radiazione, si ha un fenomeno di luminescenza analogo alla fluorescenza molecolare, ma nel caso degli atomi la radiazione riemessa è uguale o molto simile a quella eccitante, essendo assenti fenomeni di decadimento non radiativo legati alle vibrazioni molecolari. Con le sorgenti convenzionali l’eccitazione non è selettiva: gli atomi vengono portati in numerosi stati eccitati, da cui decadono dando vita a una moltitudine di righe spettrali, corrispondenti alla ricchezza dei livelli energetici (crescente all’aumentare del numero atomico). La funzione delle sorgenti è, prima ancora che eccitare gli atomi, quella di produrli, mediante la vaporizzazione e la dissociazione dei campioni (se si tratta di fasi condensate o molecole). Le varie sorgenti si differenziano tra loro per la temperatura raggiunta e quindi per il tipo di eccitazione che esse producono. Se la temperatura supera i 7000-8000 °C, buona parte degli atomi è ionizzata, per cui lo spettro osservato è dovuto principalmente all’emissione degli ioni ed è strutturalmente diverso da quello prodotto dagli atomi neutri (i livelli energetici degli ioni sono diversi da quelli degli atomi). Un importante tipo di s. di emissione, messo a punto negli anni 1970, è la s. di emissione a plasma accoppiato induttivamente (o inductively coupled plasma, ICP), nella quale la sorgente è un plasma di argon prodotto induttivamente da radiofrequenze, con temperature di eccitazione fino a 10.000 °C.

La s. di emissione trova ampia applicazione nell’analisi chimica qualitativa e quantitativa di elementi metallici e non metallici. L’analisi qualitativa si basa sull’identificazione delle frequenze emesse: per riconoscere la presenza di un elemento, ci si basa in genere su alcune righe caratteristiche particolarmente intense. Lo sviluppo della s. ICP ha aperto la possibilità di analizzare in pochi minuti decine di elementi coesistenti in un campione, con limiti minimi di rilevabilità molto bassi (microgrammi per litro o meno). Le applicazioni quantitative si basano sulla misura dell’intensità I della radiazione emessa alle frequenze caratteristiche; essa è correlata al numero N di atomi della specie analizzata da una relazione del tipo I=KNm, dove K ed m dipendono dalla riga e dalle condizioni sperimentali.

S. laser. Studia le transizioni atomiche (e molecolari) in una vasta gamma di frequenze, con alta risoluzione spettrale ed estrema sensibilità, utilizzando le proprietà della radiazione laser; viene generalmente attuata in assorbimento, o talvolta in emissione (analizzando la radiazione emessa dal campione a seguito dell’eccitazione prodotta dalla radiazione laser). La rivelazione della struttura fine e iperfine di uno spettro è ostacolata dall’allargamento (proporzionale alla frequenza) delle righe spettrali per effetto Doppler. Con sorgenti convenzionali, pur riducendo l’allargamento Doppler mediante il raffreddamento del campione o il ricorso a fasci atomici (e molecolari) ben collimati, ortogonali alla direzione di osservazione, non è possibile risolvere strutture spettrali complesse nel visibile; si è allora spostata l’osservazione dal visibile a regioni spettrali più convenienti, con la s. a radiofrequenza, la s. di risonanza magnetica ecc., raccogliendo una gran mole di misure molto accurate. Il campo della s. ottica ad alta risoluzione è stato rivoluzionato dall’avvento delle sorgenti laser e di numerosi tipi di laser (per es., i laser a coloranti organici nel visibile) che possono essere accordati con continuità su ampi intervalli di lunghezza d’onda.

Nella s. a due fotoni è possibile indurre direttamente una transizione tra due livelli atomici (o molecolari) per assorbimento simultaneo di due (o più) fotoni. Solo le sorgenti laser forniscono radiazione sufficientemente intensa da indurre transizioni di questo tipo. L’interesse per queste transizioni è legato ai seguenti aspetti: a) le regole di selezione sono diverse da quelle per transizioni a un fotone ed è pertanto possibile eccitare stati non connessi allo stato fondamentale con transizioni a un fotone; b) l’eccitazione a due fotoni consente di usare radiazione nel visibile o nell’ultravioletto vicino, in casi in cui il processo a un fotone richiederebbe radiazione a lunghezza d’onda molto più corta; c) è possibile compensare l’effetto Doppler quando i fotoni vengono assorbiti da fasci contropropagantisi. In particolare, alla risonanza tutti gli atomi, indipendentemente dalla loro velocità, possono assorbire i due fotoni, mentre fuori risonanza gli atomi non possono assorbire due fotoni che viaggiano in direzione opposta (possono però assorbire due fotoni che viaggiano nella stessa direzione se lo spostamento Doppler ripristina la risonanza). Per ogni valore della frequenza fuori della risonanza c’è solo un gruppo di velocità atomiche che può contribuire al segnale, mentre alla risonanza il contributo può provenire da tutti gli atomi; ne segue che la forma di riga per transizioni a due fotoni è la sovrapposizione di una riga intensa e stretta (di larghezza pari alla larghezza naturale) sovrapposta a una molto meno intensa e sensibilmente più larga (larghezza Doppler). Mediante la scelta di opportune polarizzazioni per i due fasci contropropagantisi è possibile in taluni casi eliminare del tutto il fondo Doppler.

La s. risolta in tempo è basata sull’impiego di impulsi luminosi di breve durata (dell’ordine del nanosecondo o minore), prodotti generalmente ma non necessariamente da una sorgente laser, allo scopo di eccitare gli atomi e studiare l’andamento temporale dell’intensità della radiazione emessa nella diseccitazione. Sono state anche eseguite misurazioni con due laser, in modo da eccitare un determinato livello mediante due transizioni successive. Per misurazioni relative a strutture iperfini di ioni in fasci veloci, si può usare una sorgente laser continua e far intersecare al fascio di luce il fascio di ioni: se gli ioni vengono fatti viaggiare a circa 1000 km/s e la zona di interazione ha dimensioni lineari dell’ordine di 0,1 mm, il tempo di eccitazione può essere brevissimo, dell’ordine di 100 picosecondi.

Notevole sviluppo ha avuto la s. a impulsi ultracorti che consente l’analisi spettrale di processi atomici e molecolari con elevatissima risoluzione temporale, mediante l’eccitazione del campione con impulsi di luce estremamente brevi (da qualche decina a qualche centesimo di picosecondo) e la rivelazione del segnale proveniente dal campione; si ottengono così informazioni sui processi dinamici con cui il campione si riporta nello stato fondamentale. Nella tecnica ‘eccitazione e verifica’ (pump and probe), si utilizzano due impulsi di luce brevissimi il cui ritardo (che può essere spinto fino al femtosecondo) viene variato otticamente: il primo impulso, quello di eccitazione, generalmente di intensità molto elevata, interagisce con il campione producendo una ridistribuzione della popolazione di atomi o molecole fra lo stato fondamentale e quello eccitato corrispondente alla frequenza impiegata; il secondo impulso attraversa con ritardo noto (e variabile) il campione; la variazione in funzione del ritardo del coefficiente di assorbimento del campione prodotta dall’impulso di eccitazione fornisce informazioni dirette sulla cinetica di ridistribuzione dell’energia in stati eccitati di molecole poliatomiche e nei solidi.

S. a radiofrequenza. Studia le interazioni tra atomi isolati (in un fascio o allo stato di gas rarefatto) e campi elettromagnetici a radiofrequenza (cioè con frequenze minori di qualche gigahertz). Negli atomi queste frequenze sono in risonanza con alcune transizioni all’interno di strutture fini e iperfini e all’interno di uno stesso multipletto Zeeman. Data la piccola differenza di energia tra due livelli interessati a una transizione a radiofrequenza (RF), pari al prodotto hν della frequenza ν per la costante di Planck h (h= 4,1∙10−6 eV/GHz), rispetto al prodotto kT, con k costante di Boltzmann e T temperatura termodinamica (pari, a temperatura ambiente, a 2,5∙10−2 eV), le coppie di livelli all’equilibrio termico sono praticamente equipopolate e si ha quindi equilibrio tra assorbimento ed emissione stimolata. Per questo la s. a radiofrequenza (SRF) è nata per lo studio di atomi (e molecole) in fasci, con i quali è possibile separare spazialmente particelle che sono in uno dei livelli della transizione. Successivamente, con il pompaggio ottico che permette di preparare gas in condizioni di non equilibrio per quanto riguarda la popolazione dei livelli, è stato possibile estendere la SRF a gas in una cella. La SRF è di grande interesse per almeno due motivi: a) il piccolo allargamento Doppler, che è proporzionale alla frequenza, permette uno studio molto preciso dei livelli atomici e dei fattori giromagnetici; b) la piccola energia dei fotoni a RF permette di raggiungere con potenze modeste condizioni di non linearità (per questo motivo le prime esperienze di s. non lineare sono state effettuate nella SRF ed è stato possibile lavorare anche in campo ottico solo grazie all’impiego dei laser). La prima esperienza di SRF è stata realizzata in fascio da I.I. Rabi nel 1939 per la misurazione di momenti magnetici nucleari.

S. molecolare

Linee generali. Lo studio sperimentale delle transizioni che avvengono tra i livelli energetici caratteristici di una molecola, qualunque sia lo stato di aggregazione in cui essa si trovi, costituisce il più potente strumento disponibile per ottenere informazioni sulla struttura e sulle proprietà microscopiche della materia su scala molecolare. Sebbene, infatti, la meccanica quantistica offra un quadro compiuto delle leggi che regolano la dinamica dei nuclei e degli elettroni costituenti una molecola, la descrizione puramente teorica degli stati quantici molecolari è necessariamente approssimata, e si avvale spesso dei dati sperimentali di origine spettroscopica. Oltre che per studi strutturali, la s. molecolare (come quella atomica) rappresenta, grazie anche al grande sviluppo delle tecniche e della strumentazione, uno dei metodi principali per l’analisi chimica qualitativa e quantitativa di campioni anche molto complessi.

La descrizione quantomeccanica della dinamica di una molecola avente N nuclei ed n elettroni si basa su un operatore hamiltoniano Hmol, nel quale i 3N gradi di libertà nucleari e i 3n elettronici, unitamente ai gradi di libertà di spin, sono mescolati tra di loro, impedendo una descrizione semplice degli stati quantici della molecola. Grazie alla approssimazione di Born-Oppenheimer, si rende possibile la separazione del moto degli elettroni da quello dei nuclei e, successivamente, la decomposizione del moto nucleare in rotazionale e vibrazionale. Diviene perciò possibile classificare i livelli energetici di una molecola in elettronici, vibrazionali, rotazionali e di spin (➔ risonanza). È alla luce di questa classificazione che l’interpretazione degli spettri molecolari si semplifica enormemente ed è su questa base che viene generalmente suddivisa la s. molecolare. L’approssimazione di Born-Oppenheimer non sempre risulta valida, ma essa rappresenta uno strumento di fondamentale importanza per la s. molecolare in un vastissimo numero di casi, in quanto rende possibile esprimere l’energia molecolare come somma dei contributi elettronico, vibrazionale, rotazionale:

fig. 3

La struttura dei livelli energetici che ne risulta è illustrata (non in scala) a titolo di esempio per una molecola biatomica in fig. 3. Ogni livello elettronico corrisponde a una ben definita distribuzione degli elettroni nel sistema (in fig. sono riportati lo stato elettronico fondamentale e uno degli stati eccitati); per ogni data configurazione elettronica si hanno vari stati vibrazionali, corrispondenti a vibrazioni di diverso contenuto energetico che i nuclei subiscono nel campo creato dagli elettroni; per ogni stato vibrazionale, infine, la molecola si può trovare in differenti stati rotazionali, corrispondenti ai possibili valori quantizzati che può assumere il momento angolare nucleare.

Il fondamento fisico che sottostà a questa separazione è la grande differenza nell’ordine di grandezza delle energie associate alle transizioni tra gli stati quantici relativi ai vari tipi di moto; la separazione tra due livelli elettronici consecutivi è in genere dell’ordine di alcuni elettronvolt, tra due livelli vibrazionali (dello stesso stato elettronico) di 0,5-0,01 eV, tra due livelli rotazionali di circa 10⁻³-10⁻⁵ eV. Questi ordini di grandezza fanno sì che il tipo di radiazione elettromagnetica richie­sta per provocare l’eccitazione del sistema sia diversa nei tre casi (e anche che sia diversa la grandezza spettrale usualmente adoperata per descrivere gli spettri nelle varie regioni), in base alla relazione di Bohr che correla la frequenza di transizione (ν_fi) con la differenza tra l’energia del livello finale (E_f) e quella del livello iniziale (E_i), ν_fi=(E_f−E_i)/h, con h costante di Planck. Così, la radiazione coinvolta è quella ultravioletta-visibile (UV-vis) per gli spettri elettronici (raggi X nel caso in cui si provochi l’eccitazione o l’emissione di elettroni appartenenti ai livelli più interni), tradizionalmente indicata mediante la lunghezza d’onda in nanometri (per i raggi X si indica in genere l’energia in elettronvolt); quella infrarossa (IR), indicata con il numero di onde in cm^–1 o la lunghezza in micrometri, per gli spettri vibrazionali; quella delle microonde, anch’essa caratterizzata mediante il numero di onde espresso in cm⁻¹, per gli spettri rotazionali. A una transizione elettronica può accompagnarsene una vibrazionale e rotazionale (struttura vibrorotazionale degli spettri elettronici, detti anche, quando questa struttura è risolta, spettri vibronici), mentre un’eccitazione vibrazionale può comportare anche una transizione rotazionale (spettri vibrorotazionali). In ogni caso, gli spettri originati da transizioni tra livelli molecolari sono spettri di bande, caratterizzati cioè da zone più o meno ampie nelle quali la radiazione viene di preferenza assorbita, emessa o diffusa.

Alla larghezza delle bande contribuiscono vari effetti, sia di tipo omogeneo sia di tipo disomogeneo: nel primo caso l’allargamento è identico per ogni molecola del campione (vale a dire, l’interazione con un fascio monocromatico è la stessa per tutte le molecole); nel secondo caso ogni singola molecola assorbe (o emette) a una frequenza diversa, sicché lo spettro osservato è dato dalla sovrapposizione delle righe delle varie molecole. Un tipico esempio di allargamento di banda disomogeneo è quello osservato, per campioni gassosi, a causa dell’effetto Doppler. L’allargamento omogeneo è dovuto al tempo di vita dello stato eccitato, agli urti, alle interazioni tra le diverse molecole, responsabili delle graduali sovrapposizioni tra bande che si possono osservare nel passare dallo spettro di molecole gassose a quello di molecole in fase liquida o solida. L’intensità di una data banda, oltre a essere influenzata dalla probabilità intrinseca che la transizione si verifichi, dipende dalla differenza di popolazione tra il livello iniziale e quello finale e dal numero di molecole che compongono il campione (concentrazione e volume del campione); quest’ultima dipendenza è alla base delle applicazioni della s. all’analisi chimica quantitativa, e nel caso degli spettri di assorbimento è espressa spesso dalla legge di Lambert e Beer:

dove I₀ è l’intensità della radiazione incidente, α è il coefficiente di assorbimento molare, b il cammino ottico e C la concentrazione molare. La validità di questa legge decade nel caso di intensità incidenti molto elevate.

S. rotazionale o a microonde. Le transizioni riguardanti livelli energetici rotazionali coinvolgono radiazioni nel campo delle microonde, aventi cioè all’incirca lunghezza da 0,3 a 0,001 m, frequenza da 1 a 300 GHz, numero di onde da 0,03 a 10 cm⁻¹. Le eccitazioni promosse da questo tipo di radiazione sono dette di pura rotazione, in quanto avvengono senza che vari l’energia vibrazionale o elettronica della molecola. Le molecole sono libere di ruotare nello spazio solo in fase gassosa; in fase liquida le rotazioni sono disturbate dagli urti e dalle interazioni intermolecolari; in fase solida i moti rotazionali sono addirittura impediti, per cui la s. a microonde riguarda in sostanza molecole allo stato di gas o vapore. L’intensità delle varie righe spettrali dipende, oltre che dalla probabilità di transizione, dalla differenza di popolazione tra lo stato iniziale e quello finale, regolata all’equilibrio termico dalla statistica di Boltzmann; essendo la spaziatura tra i livelli dello stesso ordine di grandezza dell’energia di eccitazione termica, anche a temperatura ambiente molti livelli rotazionali sono popolati, cosicché lo spettro che ne risulta è in genere ricco di bande piuttosto intense.

L’applicazione di un campo elettrico esterno modifica le energie degli stati rotazionali, eliminando la degenerazione degli stati aventi uguale momento angolare totale ma diversa componente lungo la direzione del campo (➔ Stark, Johannes); poiché l’entità dell’interazione dipende dal valore del momento di dipolo molecolare, la s. a microonde è stata ampiamente usata per la determinazione di questa grandezza in un gran numero di molecole. Oltre che per questo scopo, la s. rotazionale trova applicazione nella determinazione della geometria delle molecole, permettendo di rilevare con alta precisione lunghezze e angoli di legame, anche in virtù della scarsa larghezza delle righe spettrali, che consente un’accurata determinazione delle frequenze di transizione. A queste applicazioni si sono aggiunte poi anche quelle analitiche: sebbene limitata a campioni gassosi, la s. a microonde è molto utile per analizzare qualitativamente e quantitativamente miscele anche complesse, essendo capace tra l’altro di distinguere la presenza di differenti isotopi e di differenti isomeri conformazionali (purché dotati di momenti d’inerzia diversi).

S. vibrazionale o nell’infrarosso. Le transizioni tra livelli elettronici vibrazionali riguardano radiazioni elettromagnetiche aventi all’incirca lunghezza da 10⁻³ a 7∙10⁻⁷ m, frequenza da 3∙10¹¹ a 4∙10¹⁴ Hz, numero di onde da 10 a 14.000 cm⁻¹. Gli stati vibrazionali di una molecola rappresentano la descrizione quantomeccanica delle vibrazioni che i nuclei subiscono intorno alle loro posizioni di equilibrio. La s. di assorbimento nell’infrarosso trova molteplici applicazioni nell’analisi strutturale e chimica, sia qualitativa sia quantitativa, di molte categorie di sostanze; essa permette di misurare accuratamente le frequenze di vibrazione, le costanti di forza e le lunghezze dei legami chimici, le costanti rotazionali, le energie di dissociazione e altri parametri chimico-fisici di molte molecole. In campo analitico, la s. vibrazionale, particolarmente nella variante FTIR (Fourier transform infrared spectroscopy) che opera in trasformata di Fourier, è applicata nel rilevamento di alcuni inquinanti atmosferici (monossido di carbonio, acido nitrico ecc.), sia su porzioni di aria prelevate con opportuno campionamento, sia direttamente in situ nell’aria inquinata, su cammini ottici di centinaia o migliaia di metri.

Un altro campo di estesa applicazione della s. IR (e FTIR) è rappresentato dall’identificazione di composti organici in fase gassosa, liquida o solida. Lo spettro IR di una molecola organica presenta alcune bande (in genere nell’intervallo 900-1300 cm⁻¹) caratteristiche dello specifico composto (ne costituiscono la cosiddetta impronta digitale) e altre bande (nella regione 650-900 e 1300-4000 cm⁻¹), caratteristiche invece dei diversi gruppi funzionali. Queste ultime segnalano la presenza nella molecola di un certo raggruppamento atomico (per es., i gruppi carbonilici mostrano una forte banda di assorbimento a 1870-1540 cm⁻¹ dovuta all’allungamento del legame C=O) e possono subire dei piccoli spostamenti in frequenza a seconda dell’intorno chimico, cioè del resto della molecola, consentendo così di trarre numerose informazioni sulla struttura del composto; quando poi due gruppi funzionali assorbono a frequenze simili tra loro, le bande risultanti subiscono forti spostamenti in frequenza e ridistribuzione delle intensità; spostamenti nelle frequenze di queste bande sono causati, inoltre, da interazioni intermolecolari o con il solvente.

S. elettronica o nell’UV-visibile. Le transizioni tra i livelli elettronici di una molecola danno origine a bande di assorbimento o emissione nella regione del visibile o dell’ultravioletto (lunghezza d’onda da 700 a 10 nm); in casi particolari, come quello di complessi a forte trasferimento di carica, le bande cadono a frequenze più basse, nella regione del vicino infrarosso. La s. di assorbimento nelle regioni dell’UV e del visibile viene largamente applicata in chimica analitica, soprattutto per l’analisi quantitativa di campioni in soluzione, mediante la legge di Lambert e Beer. Spesso la sostanza da determinare viene fatta reagire con un adatto reagente in modo da trasformarla in un composto dotato di assorbimento intenso e caratteristico, e determinata così per via indiretta. In molecole organiche taluni gruppi funzionali (gruppi carbonilici, aromatici, doppi legami coniugati ecc.) sono responsabili di forti bande di assorbimento che ne consentono il riconoscimento. Oltre che per scopi puramente analitici, la s. UV-visibile trova applicazione nello studio dei composti di coordinazione, nella determinazione delle velocità e dei meccanismi di reazione ecc.

fig. 4

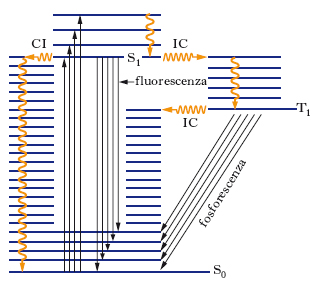
Rientra nella s. elettronica anche l’analisi spettrale della radiazione emessa da molecole per luminescenza. Quando una molecola che ha subito una transizione ad un livello elettronico eccitato ritorna allo stato fondamentale emettendo radiazione elettromagnetica, hanno luogo fenomeni di luminescenza; in particolare, se la fonte di eccitazione è una radiazione (fotoluminescenza), si hanno due meccanismi attraverso i quali può avvenire la diseccitazione: la fluorescenza e la fosforescenza. La fig. 4 illustra lo stato fondamentale S₀ e due possibili stati eccitati, S₁ e T₁ (ciascuno con la sua struttura di livelli vibrazionali); S e T sono simboli riferiti allo stato complessivo di spin (elettronico) del sistema: S indica spin totale pari a zero (stato di singoletto), T spin totale pari a 1 (stato di tripletto). La fluorescenza corrisponde in generale a transizioni in cui non si ha variazione dello stato di spin (S₁→S₀), mentre la fosforescenza corrisponde a transizioni in cui lo spin varia (T₁→S₀). In entrambi i casi, le transizioni possono avvenire da ogni livello vibrazionale dello stato eccitato a ogni livello vibrazionale di quello fondamentale. Tuttavia, sebbene l’eccitazione iniziale possa portare le molecole in stati caratterizzati da elevato valore del numero quantico vibrazionale, si ha spesso (soprattutto per molecole di elevate dimensioni e per sistemi non diluiti) un rapido decadimento non radiativo che porta la maggioranza delle particelle nello stato vibrazionale fondamentale dello stato elettronico eccitato; da qui ha poi luogo il decadimento radiativo, che avviene quindi a una frequenza inferiore rispetto a quella della radiazione eccitante. La fig. 4 chiarisce come, a differenza degli spettri di assorbimento, le bande vibroniche che appaiono nello spettro dipendono dalla struttura dei livelli vibrazionali dello stato elettronico fondamentale, e non di quello eccitato. I processi di fluorescenza e fosforescenza competono tra loro, e inoltre competono entrambi con i fenomeni di decadimento non radiativo (conversione interna), indicati con CI in figura. Se il processo non radiativo in cui la molecola passa dallo stato S₁ a quello T₁ (intersystem crossing, IC) è molto rapido, le molecole, in maggior parte, si troveranno nello stato di tripletto prima che possano dare luogo alla fluorescenza; dallo stato di tripletto esse possono decadere a quello fondamentale o per decadimento non radiativo o per fosforescenza.

La transizione radiativa dallo stato di tripletto a quello fondamentale di singoletto è proibita dalle regole di selezione di dipolo elettrico; tuttavia effetti di accoppiamento spin-orbita (notevoli soprattutto in molecole di massa elevata) la rendono possibile e fanno sì che il fenomeno della fosforescenza possa manifestarsi; poiché la probabilità di tale transizione rimane comunque bassa, il tempo di vita dello stato di tripletto è molto più lungo di quello del singoletto, cioè lo spopolamento del livello eccitato per mezzo della fosforescenza è lento. Per questo motivo, l’effetto di fosforescenza si può continuare a osservare anche per tempi lunghi dopo che è cessata l’irradiazione eccitante il campione. La fluorescenza, invece, è più rapida e cessa non appena viene tolta la sorgente di eccitazione; essa trova molteplici applicazioni nell’analisi chimica quantitativa grazie alla sua elevata sensibilità, che permette di rilevare concentrazioni molto piccole (dell’ordine di microgrammi per litro); in particolare, analisi per fluorescenza si effettuano in indagini biologiche (determinazione di amminoacidi, proteine, vitamine, ormoni, steroidi) e nel campo del monitoraggio ambientale (idrocarburi policiclici, composti eterociclici, anidride solforosa).

In alcuni sistemi può anche essere analizzato lo spettro di chemiluminescenza; in questo caso la radiazione viene emessa da una molecola prodottasi in uno stato eccitato a seguito di una reazione chimica; è un fenomeno poco frequente, ma proprio per questa sua caratteristica trova applicazione in analisi che richiedono elevata selettività. Per es., essa viene sfruttata per determinare la concentrazione del monossido di azoto NO nell’aria; in questo caso si sfrutta la reazione dell’NO con l’ozono, che produce diossido di azoto NO₂ in stato eccitato. La s. di chemiluminescenza si applica anche nell’analisi di microorganismi in prodotti alimentari e nell’acqua.

S. Raman. La s. Raman (➔ Raman, sir Chandrasekhara Venkata) studia lo spettro della radiazione diffusa da un campione a una frequenza diversa da quella della radiazione incidente (effetto Raman). Lo spettro di diffusione consiste di una riga intensa alla stessa frequenza della radiazione incidente, dovuta alla diffusione Rayleigh, e di una serie di righe più deboli a frequenza minore o maggiore, dovute appunto alla diffusione Raman, che si denominano rispettivamente righe Stokes e righe anti-Stokes. La differenza in frequenza tra la riga Rayleigh e una riga Raman risulta pari a una frequenza di transizione vibrorotazionale o rotazionale della molecola. La s. Raman è una s. lineare perché l’intensità delle righe dello spettro di diffusione risulta proporzionale all’intensità della radiazione incidente, ed è una s. a due fotoni perché il processo elementare coinvolge l’annichilazione di un fotone della radiazione incidente e la generazione, praticamente simultanea, di un fotone della radiazione diffusa. Processi di diffusione più complessi coinvolgenti più di due fotoni determinano spettri di diffusione differenti e, soprattutto, mostrano andamento non lineare.

In linea generale, la probabilità di transizione per la diffusione Raman è relativamente bassa; tuttavia essa cresce al crescere della frequenza della radiazione incidente (e diffusa), per cui le sorgenti utilizzate in genere appartengono alla regione del visibile. Le intensità rimangono comunque deboli: si può calcolare per es., che un campione di densità 10²⁰ molecole per cm³ e cammino ottico 10 cm diffonde circa un fotone (visibile) per ogni 10⁹ fotoni incidenti. Per questo motivo le sorgenti impiegate nella s. Raman sono sempre laser di elevata potenza. L’uso del laser ha anche un altro vantaggio: la differenza in frequenza tra le righe Raman e quella Rayleigh è percentualmente molto piccola ed è perciò desiderabile utilizzare una sorgente altamente monocromatica (come il laser), che permette di distinguere facilmente le righe Raman nello spettro di diffusione.

Grazie allo sviluppo dei laser la s. Raman ha potuto trovare un gran numero di applicazioni, anche congiuntamente alla s. IR; in quest’ultimo caso essa si presta molto bene allo studio di strutture molecolari. Per es., se una sostanza presenta almeno un modo di vibrazione attivo in entrambe le metodiche, si può subito dedurre che essa non presenta un centro di simmetria; infatti, in molecole dotate di centro di simmetria i modi di vibrazione attivi nell’IR sono inattivi nella Raman e viceversa (regola di mutua esclusione). Analogamente, si possono condurre mediante s. Raman studi di analisi conformazionale di proteine. La s. Raman trova inoltre impiego in microanalisi, nella rilevazione di inclusioni fluide in minerali, in indagini sui polimeri, nel monitoraggio di processi elettrodici (mediante l’uso di fibre ottiche), nella determinazione di energie di dissociazione ecc.

S. a raggi X. La s. a raggi X (lunghezza d’onda λ=10-10⁻² nm) coinvolge l’eccitazione o l’emissione di elettroni appartenenti ai livelli energetici più interni dell’atomo, della molecola o del solido in esame; l’energia dei fotoni X (100 eV-100 keV) è infatti tale da permettere l’eccitazione degli elettroni più strettamente legati al nucleo. I livelli energetici di questi elettroni dipendono in larga misura dal tipo di atomo cui appartengono (sono cioè caratteristici dei vari elementi); tuttavia la frequenza esatta di eccitazione per un dato elettrone può risultare leggermente modificata (chemical shift) a seconda della diversa natura degli atomi circostanti e del tipo di legame presente, consentendo l’ottenimento di numerose informazioni chimiche e strutturali. La s. a raggi X può essere basata sulla misura dell’assorbimento della radiazione da parte del campione, che segue un andamento di tipo Lambert (➔ raggio) oppure sulla determinazione dell’energia cinetica degli elettroni fotoemessi. Queste due metodiche consentono di ricavare informazioni sulla configurazione atomica locale media nell’intorno dell’atomo eccitato (in una sfera di qualche Å); sviluppatesi soprattutto dopo l’introduzione della radiazione di sincrotrone, le due tecniche sono impiegate nel campo della fisica dei solidi, della biochimica, della catalisi, dello sviluppo di nuovi materiali ecc.

S. nucleare

fig. 5

I nuclei di ciascun isotopo emettono e assorbono radiazione elettromagnetica, generalmente raggi γ, solo in corrispondenza di certi valori ben definiti della frequenza tipici del nuclide. La generica capacità dei nuclei di emettere e assorbire radiazione elettromagnetica è dovuta alla presenza al loro interno di particelle elettricamente cariche, i protoni, legate tra loro e ai neutroni da interazioni forti. Come nel caso della s. atomica, l’interpretazione degli spettri nucleari è immediata in termini di livelli energetici e di transizioni tra di essi: a ciascun nucleo è associato un insieme discreto di stati con ben determinati valori dell’energia o livelli energetici. Le frequenze delle righe spettrali sono dell’ordine di 105 volte maggiori che nel caso degli spettri atomici perché le differenze di energia tra gli stati nucleari, essendo determinati dalle interazioni forti che sono molto più intense di quelle elettromagnetiche che presiedono alla struttura elettronica dell’atomo, sono all’incirca 105 volte più grandi di quelle atomiche (frazioni di megaelettronvolt contro qualche elettronvolt). Anche in questo caso, lo studio degli spettri nucleari è di fondamentale importanza per la comprensione della fisica del nucleo atomico, perché consente di risalire ai livelli energetici che sono una fonte di informazione diretta sulla dinamica interna del nucleo, come anche fornisce (per l’assenza di talune righe, la presenza di multipletti ecc.) informazioni sul momento angolare dei nuclei. In fig. 5 è riportato lo schema dei livelli energetici del nucleo del boro (105B); il primo numero alla destra di ciascun livello è il valore dello spin seguito dall’indicazione della parità (+,−), il secondo è lo spin isotopico; le linee verticali indicano le principali transizioni (nelle quali vengono emessi fotoni γ). Gli spettri nucleari possono essere studiati in dettaglio eccitando i nuclei atomici con fasci di particelle (in particolare elettroni o protoni) con energia dell’ordine di diversi megaelettronvolt.

S. adronica

fig. 6

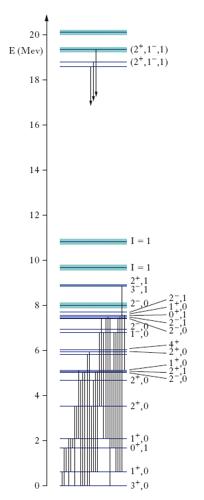
Un nucleone (protone o neutrone) isolato, quando assorbe un’energia sufficientemente elevata (almeno ≃140 MeV, energia equivalente alla massa a riposo del pione), può compiere una transizione verso uno stato fortemente instabile a maggior contenuto energetico (detto anche risonanza); ritorna poi nel suo stato fondamentale con l’emissione di uno o più mesoni (in particolare pioni) o molto più raramente con l’emissione di un fotone gamma. L’eccitazione del nucleone viene eseguita mediante fasci di particelle (fotoni, pioni, protoni ecc.) di alta energia. Studiando questi stati, la cui separazione energetica è tipicamente dell’ordine di 102 MeV, si costruiscono schemi di livelli come quello in fig. 6. Fenomeni analoghi si hanno anche con adroni diversi dal nucleone. Data la grande energia di eccitazione e le grandi differenze di energia tra questi stati, per l’equivalenza energia-massa, questi stati hanno masse sensibilmente diverse e possono essere classificati, oltre che con i numeri quantici che li caratterizzano, proprio con il valore della loro massa. Così come la s. atomica ha indicato la presenza nell’atomo di una struttura (costituita dagli elettroni e dal nucleo) e la s. nucleare nel nucleo (costituita da protoni e neutroni), la s. adronica ha suggerito che il nucleone e più in generale gli adroni avessero una struttura interna, costituita dai quark (➔ particelle elementari).

S. astronomica

Le tecniche spettroscopiche rivestono enorme importanza in astrofisica, in quanto consentono di studiare la composizione spettrale (spettro) delle sorgenti astronomiche. Gli spettri continui vengono generati termicamente (radiazione di corpo nero) da corpi con spessore ottico notevole (alta densità e opacità alla luce) quali stelle, pianeti, nubi di polvere interstellare. Gli spettri di righe possono essere di assorbimento o di emissione. Nel primo caso si tratta di solito di nubi di gas illuminate da una sorgente a spettro continuo retrostante. All’osservatore arriva lo spettro continuo della sorgente retrostante, privato delle lunghezze caratteristiche delle transizioni degli atomi, ioni o molecole presenti nella nube di gas. Esempio tipico di questa situazione sono le cosiddette righe di assorbimento presenti nello spettro del Sole, osservate per la prima volta da J. Fraunhofer. Lo spettro continuo (approssimativamente di corpo nero) della luce solare viene generato dalle regioni più profonde (e quindi più calde) del Sole. Le righe di assorbimento sono dovute alla presenza di atomi e ioni negli strati più esterni del Sole (e quindi più freddi). Se l’osservatore non è allineato alla direzione sorgente-nube, egli osserva solo la luce riemessa dai costituenti della nube, e non quella della sorgente continua che illumina la nube. In questo caso, poiché i costituenti della nube riemettono solo le lunghezze d’onda caratteristiche che avevano assorbito, si osserverà uno spettro costituito da righe brillanti su sfondo nero, cioè uno spettro di emissione. Se il gas della nube è molto caldo, la nube produce uno spettro di righe in emissione senza bisogno di alcuna sorgente di illuminazione.

L’analisi delle lunghezze d’onda delle righe spettrali permette l’identificazione dei costituenti della nube in studio. Inoltre, l’intensità delle righe consente di stimare la quantità di ciascuna delle specie costituenti, mentre il confronto di righe diverse caratteristiche della stessa specie costituente consente di stabilirne la temperatura. L’effetto Doppler modifica le lunghezze d’onda delle righe spettrali di una quantità proporzionale alla velocità relativa sorgente-osservatore, lo spostamento della lunghezza d’onda Δλ essendo proporzionale alla velocità v e alla lunghezza d’onda λ: Δλ=λv/c, con c velocità della luce. Le osservazioni spettroscopiche permettono quindi anche di misurare le velocità di allontanamento o di avvicinamento delle sorgenti astronomiche. Per es., lo spettro della stella Vega mostra una ‘prominente’ riga Hα dell’idrogeno: la lunghezza d’onda risulta essere di 656,255 nm, mentre in laboratorio la riga Hα ha una lunghezza d’onda di 656,285 nm. Usando la formula dell’effetto Doppler se ne conclude che lo spostamento verso il blu (lunghezze d’onda più brevi), pari a Δλ=0,030 nm, è determinato da una velocità di avvicinamento di Vega pari a v=cΔλ/λ=13,7 km/s, che corrisponde alla componente della velocità della stella nella direzione della linea di vista (velocità radiale). La componente tangenziale della velocità non produce effetto Doppler, e quindi non è misurabile con metodi spettroscopici. Un altro esempio di spostamento delle righe spettrali è il redshift (o spostamento verso il rosso) delle galassie lontane, dovuto alla espansione generale dell’Universo (➔ cosmologia).

La s. della luce proveniente dai pianeti permette di determinare i gas costituenti le loro atmosfere (anidride carbonica per Venere; idrogeno, elio, metano, ammoniaca e acqua in Giove e Saturno; ghiaccio d’acqua nei satelliti galileiani di Giove; ecc.). In quest’ambito l’analisi spettroscopica viene effettuata specialmente a lunghezze d’onda infrarosse, dove risiede un grande numero di righe rotazionali e vibrazionali delle molecole costituenti le atmosfere.

Lo studio ad altissima risoluzione dell’effetto Doppler della luce proveniente dal Sole (➔) ha permesso di evidenziare la presenza di oscillazioni solari, cioè di pulsazioni periodiche della fotosfera solare, dovute a onde di compressione che si propagano all’interno del Sole. Soltanto le onde che risuonano all’interno del Sole possono generare un significativo effetto Doppler, per cui lo studio dettagliato di queste oscillazioni è il metodo più importante di studio dell’interno del Sole (eliosismologia).

Le stelle sono classificate proprio in base ai loro spettri, che sono una sovrapposizione di spettri continui e di righe. Lo spettro continuo, all’incirca di corpo nero, consente di risalire alla temperatura superficiale della stella, che va da più di 30.000 K per le stelle di tipo O a meno di 3000 K per stelle di tipo M. Queste diverse temperature sono responsabili dei vari colori delle stelle, a causa dello spostamento della lunghezza d’onda di massima emissione dall’ultravioletto per stelle di tipo O (che quindi appaiono blu) a circa 400 nm per stelle di tipo G come il Sole (che quindi appaiono gialle), all’infrarosso per stelle di tipo M (che quindi appaiono rosse). Le righe sovrapposte allo spettro continuo sono indice dello stadio evolutivo delle stelle. Per le stelle di tipo O (da 20.000 a 35.000 K di temperatura superficiale) sono presenti righe di atomi ionizzati molte volte (per es., He II, C III, N III, O III, Si V), mentre le righe dell’idrogeno sono deboli (perché è in gran parte ionizzato). Per le stelle di tipo B (ca. 15.000 K) l’He II è scomparso, ci sono O II, Si II e Mg II e si cominciano a vedere le righe dell’idrogeno. Per le stelle di tipo A (9000 K) le righe dell’idrogeno dominano lo spettro, e non è più visibile l’elio. Per le stelle di tipo F (≃7000 K) le righe dell’idrogeno sono più deboli, mentre si cominciano a vedere il Ca II, il Fe I, Fe II, Cr II e Ti II. Per le stelle di tipo G (5500 K, come il Sole) sono sempre più importanti le righe dei metalli. Nel caso del Sole, già Fraunhofer aveva osservato circa 600 righe. Alla metà degli anni 1990 se ne era arrivati a conoscere intorno a un milione. Per le stelle di tipo K (≃4000 K) lo spettro è dominato da righe dei metalli, è forte il Ca I e si cominciano a vedere righe del TiO. Le stelle rosse di tipo M (≃3000 K) hanno bande di righe del TiO ‘prominenti’ e del Ca I.

Le galassie hanno uno spettro complesso, che è somma di una componente dovuta alle stelle costituenti e di un’altra componente dovuta al mezzo interstellare (➔ gas). Questo è costituito a sua volta da uno spettro continuo dovuto alle polveri e da uno spettro di righe dovuto ad atomi e molecole.

Particolarmente importante per lo studio del mezzo interstellare è la s. radioastronomica, che permette, per es., di studiare la distribuzione dell’idrogeno neutro per mezzo dell’osservazione della riga iperfina dell’atomo di idrogeno, a una lunghezza d’onda di circa 21 cm. Inoltre, la radioastronomia millimetrica e submillimetrica ha consentito di catalogare un grandissimo numero di composti molecolari sia inorganici sia organici presenti nel mezzo interstellare. Lo studio della formazione ed evoluzione di questi elementi e della loro rilevanza nei processi evolutivi galattici è detto astrochimica.

Attraverso la s. applicata a oggetti extragalattici si sono evidenziate le enormi velocità di allontanamento di sorgenti cosmologiche. Un esempio tipico sono i quasar (➔). Per es., lo spettro del quasar 3C273 mostra evidentissime quattro righe di emissione. Queste corrispondono alle prime quattro righe della serie di Balmer dell’idrogeno neutro, tutte con lunghezza d’onda spostata di circa il 16% rispetto alle lunghezze d’onda misurate in laboratorio. Se interpretato come effetto Doppler, questo fatto implica una velocità apparente di allontanamento di circa 45.000 km/s. Velocità di allontanamento così enormi sono state trovate sistematicamente per tutte le sorgenti più lontane, portando all’ipotesi dell’espansione dell’universo.

Altri tipi di spettroscopia

S. Auger. Analisi spettrale, effettuata con uno spettrometro per elettroni, dell’emissione elettronica conseguente all’effetto Auger (➔ Auger, Pierre Victor).

S. in derivata. Metodica consistente nel produrre e rappresentare uno spettro riportando la derivata prima o seconda dell’intensità della radiazione (anziché l’intensità stessa) in funzione di una grandezza spettrale. Questa rappresentazione può permettere di rilevare con maggior facilità dettagli spettrali non sufficientemente evidenti nella rappresentazione tradizionale.

S. interferenziale. Metodo che utilizza gli interferometri per eseguire analisi spettrali con altissimo potere risolutivo; si basa sul fatto che l’interfrangia in una figura di interferenza (➔) è direttamente proporzionale alla lunghezza d’onda della radiazione. Nel visibile è particolarmente impiegato l’interferometro di Fabry e Perot.

S. neutronica. L’insieme delle tecniche di analisi strutturistica fondate sulla diffrazione di fasci di neutroni ad opera di sostanze materiali.

S. in trasformata. Le misure tradizionali in s. atomica (e molecolare) richiedono la determinazione dell’intensità della radiazione in uscita dal campione in un certo numero n di intervalli spettrali; ciò viene fatto, in generale, eseguendo una scansione nel campo di frequenze che interessa esaminare, facendo giungere sul rivelatore, di volta in volta, ciascuno degli intervalli spettrali. Nella s. in trasformata, invece, un unico rivelatore vede nello stesso istante gli n elementi spettrali, raccogliendo un segnale che non rappresenta direttamente le n intensità richieste, ma una loro combinazione lineare; la determinazione delle singole intensità e frequenze spettrali viene ottenuta a partire da questo segnale attraverso un’operazione matematica, ed è resa possibile dal fatto che il segnale di ciascun elemento spettrale, che costituisce una componente di quello complessivo, è contraddistinto da una specifica modulazione che lo distingue dagli altri. Tra le s. in trasformata, quella che ha avuto il maggior impatto, e che ha sostituito in molte applicazioni le tecniche tradizionali, è la s. in trasformata di Fourier (o s. FT, Fourier transform), che è caratterizzata dall’uso di modulazioni sinusoidali. Nella s. FT per assorbimento, il campione viene attraversato da una radiazione elettromagnetica ‘bianca’ (policromatica), opportunamente generata con modulazione sinusoidale molto spesso mediante un interferometro di Michelson; il campione assorbe in varia misura alcune delle componenti della radiazione, e ne lascia passare la parte rimanente, che raggiunge il rivelatore, dove viene rilevata l’intensità in istanti successivi (con intervalli di un millisecondo o meno); i dati vengono immagazzinati da un elaboratore e trattati matematicamente secondo gli algoritmi della trasformata di Fourier; questa operazione permette di ottenere lo spettro nella forma tradizionale (nel dominio cioè delle frequenze), a partire dal segnale rilevato (che è un complesso interferogramma delle varie componenti spettrali non assorbite, ciascuna con la sua frequenza e la sua ampiezza). La s. FT presenta alcuni vantaggi rispetto alle s. tradizionali: essa permette un miglioramento del rapporto segnale-rumore pari, se il rumore non dipende dal segnale, a (n/8)1/2, dove n è il rapporto fra il tempo di operazione di una scansione completa nel dominio delle frequenze e quello necessario a raccogliere il segnale, e il fattore 8 rappresenta la perdita di intensità dovuta alla modulazione; questo vantaggio, detto vantaggio multiplex, è molto rilevante, perché si possono raggiungere valori di n anche di 105-106; un secondo vantaggio è quello detto di luminosità, derivante dal fatto che la radiazione registrata dal rivelatore copre un angolo solido molto più ampio di quello ottenibile con gli strumenti a dispersione; grazie ai brevissimi tempi necessari per la rivelazione del segnale, inoltre, è possibile studiare specie transienti soggette a rapida decomposizione o trasformazione (per es., intermedi di reazioni chimiche); la s. in trasformata di Fourier, infine, si presta per sua natura alla realizzazione di vantaggiosi interfacciamenti con calcolatore, che rendono agevoli numerose operazioni (sottrazione dello spettro ottenuto dalle bande caratteristiche del solvente, integrazione delle aree dei picchi ecc.).

La s. in trasformata di Fourier ha trovato larga applicazione soprattutto nell’assorbimento infrarosso, a causa della maggiore difficoltà nel trovare sorgenti e rivelatori efficienti in ampi intervalli di frequenza, e nella risonanza magnetica nucleare.