termodinamica
Parte della fisica che studia i processi macroscopici implicanti scambi e conversioni di calore; lo studio termodinamico, puramente fenomenologico, descrive i sistemi fisici con un numero limitato di parametri, misurabili macroscopicamente e tra i quali sussistono relazioni determinabili sperimentalmente. Alla base della t. è l’equivalenza fra calore e lavoro.
Sviluppo storico
L’avvio della t. classica. La t. classica fu formulata a metà circa del 19° secolo. I fenomeni termici erano interpretati, fin dalla metà del 18° sec., in base a delle forze a breve raggio agenti tra le particelle del ‘calorico’ e tra queste e quelle della materia. Il principio di conservazione dell’energia si diffuse da circa metà Ottocento in seguito a scoperte sperimentali che legavano fra loro elettricità, magnetismo, luce, calore, affinità chimica e forze meccaniche. Esse fecero supporre che l’azione di un ‘agente’ naturale si potesse trasformare in quella di un altro in misura in qualche modo equivalente. Grazie allo studio delle macchine (in particolare termiche), si riconsiderò l’idea che la ‘forza viva’ del moto, in apparenza perduta per gli attriti, si manifestasse in forma di calore. Dovendosi però ammettere che il calore possa crearsi e non solo trasferirsi e dato che una sostanza (il fluido calorico) non può né crearsi né distruggersi, si dovette tornare all’idea del 17° sec. per cui il calore (➔) è una forma di movimento. L’idea della conservazione delle ‘forze’ naturali applicata ai fenomeni termici segna l’avvio della t. classica ed è alla base della formulazione del suo primo principio.
J.P. Joule, le cui prime ricerche riguardarono fenomeni elettrochimici (l’effetto Joule è quello per cui il passaggio di corrente elettrica produce calore), studiando il rendimento dei motori elettrici, mise in relazione le ‘forze’ chimiche sviluppate nella pila, l’intensità delle correnti prodotte, i loro effetti termici e meccanici, e realizzò catene di conversione in cui degli ‘agenti’ naturali erano correlati tra loro e si trasformavano l’uno nell’altro. Joule si convinse che calore ed effetto meccanico potevano convertirsi direttamente l’uno nell’altro: nelle macchine idrauliche e meccaniche la potenza meccanica perduta per attrito si trasformava in calore mentre in quelle termiche si produceva un effetto meccanico, consumando una quantità equivalente di calore. Joule dimostrò che facendo perdere per attrito la capacità di compiere lavoro, per es. di una massa posta a una data altezza e lasciata cadere, si otteneva sempre la stessa quantità di calore e così determinò l’equivalente meccanico del calore.
Il primo e il secondo principio della termodinamica. Secondo Joule si poteva completamente convertire calore in lavoro meccanico e viceversa. Tale principio di equivalenza non bastava a risolvere tutti i problemi posti dallo studio delle macchine termiche. Nel 1824 S.-N.-L. Carnot aveva pubblicato un trattato sul funzionamento delle macchine termiche in cui erano contenute le idee all’origine della teoria termodinamica: tra queste, l’idea base che una macchina termica, per produrre lavoro meccanico usando calore (per es. sviluppato nella combustione), deve lavorare almeno tra due sorgenti a temperatura diversa. Secondo Carnot, il calore produce lavoro perché passa spontaneamente dalla sorgente più calda a quella più fredda. Inoltre, una macchina termica reversibile può funzionare al contrario, usando lavoro per far ‘salire’ il calore dalla sorgente fredda a quella ‘calda’, e creando una differenza di temperatura tra due corpi. Il teorema di Carnot stabiliva un valore per il rendimento di una macchina termica reversibile, dipendente unicamente dalle temperature delle sorgenti – quindi, uguale per tutte le macchine, purché reversibili – tra le quali la macchina lavora e non dalla natura del fluido impiegato.
Oltre vent’anni più tardi, la teoria di Carnot fu ripresa da W. Thomson (futuro lord Kelvin), anche se essa sembrava contraddire il principio di conservazione dell’energia, che allora si affermava. Infatti, se calore e lavoro erano equivalenti, non era chiaro perché servisse una differenza di temperatura per avere con continuità lavoro dal calore, né perché, se la differenza di temperatura si annullava, la capacità del sistema di compiere lavoro andasse perduta. Tali problemi apparivano insolubili a Thomson nel 1848, quando in base della teoria di Carnot introduceva il concetto di temperatura termodinamica.
Nel 1850, R.J.E. Clausius trovò la soluzione: egli distinse tra l’energia contenuta in un corpo, che era una funzione di stato, e il calore o il lavoro trasferiti al o dal corpo, dipendenti dalla trasformazione dal corpo subita. Il primo principio della t. stabiliva che la variazione di energia interna U di un corpo era pari all’energia scambiata con l’esterno (come calore o lavoro) e che quindi, in un ciclo, lo scambio di calore doveva essere equivalente a quello di lavoro. Clausius si accorse che, per accordarsi con il principio di equivalenza di Joule, la teoria di Carnot andava modificata solo in parte. Per dimostrare il teorema di Carnot, formulò il suo enunciato del secondo principio della t., per il quale non si può avere in natura un processo il cui unico risultato sia il trasferimento di una certa quantità di calore da un corpo più freddo a uno più caldo. Nel 1851 Thomson propose il secondo assioma fondamentale della teoria per cui non si può produrre lavoro utile da un corpo raffreddandolo al di sotto della temperatura del più freddo dei corpi circostanti.
Subito dopo la formulazione dei due principi della t., Clausius introdusse il concetto di entropia. Dapprima egli riformulò la seconda legge come un principio di equivalenza delle trasformazioni. Con la definizione dell’entropia come S=ʃdQ/T (per una trasformazione reversibile), dal 1865 il secondo principio diviene per Clausius sinonimo di principio dell’aumento di entropia, enunciato nella nota forma «l’entropia dell’universo tende a un massimo».
Negli anni 1870 J.W. Gibbs indicò con alcuni lavori le straordinarie possibilità di generalizzazione della t., in particolare nei riguardi della chimica (per es. egli dedusse la regola delle fasi). Gibbs concepiva in generale ogni trasformazione termodinamica in termini di trasferimento di energia e/o materia. Solo al trasferimento di calore si associava un trasferimento di entropia (per cui si poteva porre, per una trasformazione infinitesima reversibile, δQ=TdS). In base a ciò, egli integrava i due principi della t. nell’assunzione generale che, per un sistema isolato, l’entropia tende a un massimo a energia costante o, in alternativa, l’energia tende a un minimo a entropia costante.
I risultati di Clausius e Gibbs furono raccolti e integrati da M. Planck, le cui Vorlesungen über Thermodynamik, del 1897, costituiscono la formulazione più compiuta della t. classica. In esse, la teoria diviene una generale teoria fenomenologica dei processi in cui ha un ruolo la variabile temperatura. Planck considerò centrale la funzione entropia (il cui ruolo era ancora in parte non riconosciuto dai contemporanei, in particolare dalla scuola detta energetista): in natura vanno distinti i processi naturali, in cui l’entropia totale (sistema + ambiente) comunque aumenta, e i processi neutrali, che sono solo finzioni mentali, in cui l’entropia totale non varia e che avvengono solo in condizioni ideali. L’irreversibilità dei processi naturali è il dato fenomenologico di partenza, difficilmente riconducibile ai processi solo meccanici postulati dalla teoria cinetica dei gas. Planck inoltre con;tribuì in misura rilevante all’applicazione della t. alla chimica e alla teoria delle soluzioni diluite.
Il terzo principio della termodinamica. Un altro sviluppo interessante sarebbe derivato dall’applicazione della t. allo studio della reattività chimica, che, con i contributi di Gibbs, H. von Helmholtz, H.-L. Le Châtelier, aveva esteso le potenzialità dell’approccio termodinamico nello studio della possibilità, della direzione e dello stato finale di equilibrio delle reazioni chimiche. Tuttavia, a fine secolo, i problemi aperti erano ancora molti. In particolare, andava stabilita la relazione esatta tra variazione di energia libera ΔA e variazione del calore di reazione (entalpia) ΔH per le varie temperature a cui avveniva una reazione. W. Nernst affrontò il problema dal punto di vista teorico e sperimentale e formulò il terzo principio della termodinamica. In pratica, Nernst stabilì che le curve che rappresentavano ΔA e ΔH in funzione della temperatura divenivano tra loro tangenti allo zero assoluto. Perciò, tendendo allo zero assoluto, la variazione di entropia doveva tendere ad annullarsi (Nernst asseriva che lo zero assoluto è un limite di fatto irraggiungibile). Questa condizione era sufficiente a prevedere gli equilibri chimici. Conosciuti i primi lavori di A. Einstein sulla fisica dei quanti, Nernst vide la connessione del suo teorema con la teoria quantistica dei calori specifici: da allora il teorema di Nernst contribuì decisamente all’affermazione delle idee di Planck e Einstein sulla quantizzazione dell’energia.
Un ulteriore contributo alla formulazione della t. classica fu, all’inizio del 20° sec., quello di M. Born e C. Carathéodory, che, studiando le proprietà analitiche delle equazioni che sintetizzavano i principi della t., proposero una nuova assiomatizzazione della teoria, con la definizione delle grandezze fondamentali in termini puramente operativi. La nuova formulazione assiomatica della seconda legge della t. si riferiva al principio di inaccessibilità adiabatica di Carathéodory: in prossimità di uno stato, comunque fissato, di un qualsiasi sistema termodinamico esistono sempre alcuni stati non raggiungibili, a partire dallo stato dato, tramite una qualsiasi trasformazione adiabatica.
Il secondo principio della t. almeno fino alla fine del 19° sec. trovò sia oppositori sia sostenitori. Ciò perché per i fisici di metà Ottocento era la meccanica la teoria fondamentale della fisica; il secondo principio si riferiva a una direzionalità spontanea dei processi naturali e sembrava inconciliabile con l’invarianza per inversione temporale delle equazioni della meccanica. Tale difficoltà di conciliazione fu messa in risalto nel 1871 da J.C. Maxwell, con il suo esperimento mentale del demone ordinatore (il celebre diavolo di Maxwell). Un essere così piccolo da poter osservare e maneggiare le singole molecole, trovandosi in un recipiente, diviso in due comparti A e B da una parete con uno sportello e contenente un gas inizialmente all’equilibrio, avrebbe potuto selezionare le molecole più veloci in A, lasciandole passare in B, e le molecole più lente in B, lasciandole passare in A; supponendo che l’apertura e la chiusura dello sportello non comportasse lavoro meccanico, si concludeva che tale essere avrebbe prodotto una differenza di temperatura in un sistema inizialmente in equilibrio termico senza spesa di lavoro meccanico. Quindi, per un essere capace di operare a livello microscopico, il secondo principio non ha significato: l’irreversibilità della dissipazione dell’energia dipenderebbe solo dal fatto che la nostra scala macroscopica di osservazione e di intervento non ci fa distinguere le singole molecole e operare su di esse. Per Maxwell, quindi, il fatto che i sistemi fisici fossero in ultima analisi sistemi meccanici faceva sì che il secondo principio valesse solo alla nostra scala di osservazione. Alcuni fisici, come Planck, escludevano di poter ricondurre il secondo principio alle leggi della meccanica per l’impossibilità di ritrovare l’irreversibilità caratteristica dei processi termodinamici. Per altri fisici e chimici, come E. Mach e W. Ostwald, per i quali solo le variazioni di energia erano direttamente osservabili, il secondo principio era un caso particolare del principio di conservazione dell’energia. Contro tale tendenza energetista, L. Boltzmann tentava di trovare una spiegazione meccanico-atomistica del secondo principio e di dimostrare la tendenza spontanea di un sistema meccanico, composto da un grandissimo numero di costituenti elementari, a raggiungere una configurazione di equilibrio, caratterizzata (nel caso di un gas) dalla distribuzione maxwelliana delle velocità molecolari. Il suo programma di ricerca portò a una straordinaria innovazione concettuale: il secondo principio esprimeva la tendenza del sistema ad assumere la configurazione macroscopica più probabile, ossia quella cui corrispondeva il numero di gran lunga più elevato degli stati microscopici compatibili con i vincoli imposti al sistema stesso. L’entropia di Boltzmann era legata a tale probabilità, secondo la relazione di Boltzmann S=klnW, dove W rappresentava appunto il numero di stati microscopici, o di complessioni. La validità della concezione cinetico-atomistica fu chiara quando accurate ricerche sperimentali misero in evidenza le fluttuazioni che si manifestavano anche a scala osservabile, per es. nel fenomeno del moto browniano, in un sistema in condizioni di equilibrio termodinamico.
T. statistica. Grazie anche ai contributi di Gibbs dei primi anni del 20° sec., l’interpretazione microscopica dei principi della t. apriva un nuovo settore della fisica, chiamato da allora meccanica statistica (➔ meccanica), basata su assunzioni probabilistiche. L’estensione della t. allo studio delle fluttuazioni casuali, e quindi lo spostamento dell’attenzione verso un livello mesoscopico, intermedio tra quelli macroscopico e microscopico, diede origine a un settore della fisica statistica, distinto dalla meccanica statistica, denominato t. statistica.
La t. classica faceva riferimento a stati di equilibrio; era cioè una termostatica, in cui non compariva la variabile temporale. Lo studio dei processi irreversibili (o processi dissipativi), in cui si verificava una tendenza spontanea a raggiungere uno stato di equilibrio, si limitava al confronto tra stato iniziale e stato finale. In verità, per processi quali la conduzione termica o la diffusione, alcune trattazioni fenomenologiche già descrivevano il loro andamento temporale con leggi di trasporto di analoga struttura. Tali leggi si riferivano al flusso di una variabile estensiva (il calore nella conduzione, la quantità di materia nella diffusione) e lo ponevano in relazione alla differenza di una variabile intensiva (rispettivamente temperatura T e potenziale chimico μ). Lo studio sistematico di questi processi fu possibile una volta disponibili, grazie soprattutto a Gibbs, le relazioni tra variazioni di energia e di entropia e variazioni di altre variabili estensive (con le intensive coniugate). Per passare dagli stati ai processi la rappresentazione doveva tener conto delle variazioni nello spazio e nel tempo delle variabili termodinamiche, considerandole variabili di campo come quelle della dinamica dei fluidi. Punti dello spazio e istanti erano in realtà pensati come elementi di volume o intervalli temporali così grandi da poter assumere che al loro interno si avesse equilibrio termodinamico (equilibrio locale). I processi che portano irreversibilmente a uno stato di equilibrio erano rappresentabili in termini di flussi delle variabili estensive, guidati da differenze di variabili intensive (forze generalizzate). L. Onsager formulò la teoria completa di questi processi, in condizioni non lontane dall’equilibrio, nel 1931. Nel 1947 I. Prigogine formulò il teorema di minima produzione di entropia, per cui, se si verificano condizioni che impediscono al sistema di raggiungere l’equilibrio (per es., nel caso di sistemi aperti), i processi stazionari, in condizioni vicine all’equilibrio, tendono a stabilizzarsi in modo che la produzione di entropia a essi associata raggiunga un valore minimo. Questo teorema rende possibile applicare la t. dei processi allo studio delle strutture dissipative e dei connessi fenomeni di auto-organizzazione.
Sistemi termodinamici e trasformazioni
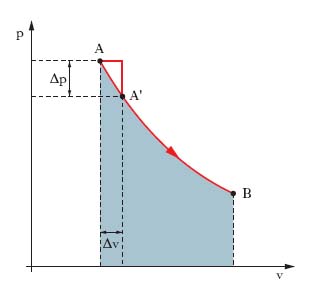
La descrizione di un sistema materiale costituito da molti componenti si può fare mediante grandezze istantanee (coordinate, velocità, massa) relative ai singoli componenti o mediante grandezze globali (massa complessiva, volume, pressione), misurabili macroscopicamente, dette variabili, o parametri di stato (➔), e il sistema così descritto è detto sistema termodinamico. Tra le variabili di stato sussistono relazioni dette equazioni di stato. Un sistema termodinamico, non interagente con l’esterno abbastanza a lungo, raggiunge uno stato di equilibrio termodinamico, in cui i parametri di stato sono uniformi e costanti nel tempo. Una trasformazione t. è un qualunque processo per cui un sistema si porta da uno stato di equilibrio t. a un altro, essendovi tra il sistema e l’esterno scambi di energia, la cui entità dipende da due variabili di stato, una intensiva (indipendente dall’estensione del sistema), l’altra estensiva. Uno scambio implicante lavoro fatto da forze di pressione (per es. durante un’espansione) è descrivibile quantitativamente mediante la pressione (grandezza intensiva) e il volume (grandezza estensiva); per un trasferimento di calore si considerano temperature (intensive) ed entropie (estensive) ecc. La trasformazione di una massa di gas descritta dalle tre variabili di stato p, v, T si rappresenta per es. con una linea, nel piano cartesiano ortogonale (v, p), noto come piano di Clapeyron, congiungente i punti A, B (fig. 1) rappresentativi degli stati di equilibrio iniziale e finale, rispettivamente. Se si aumenta, a partire dallo stato iniziale A, il volume di pochissimo, Δv, e si attende il tempo, anche molto lungo, dopo il quale la pressione, diminuendo di Δp, assume lo stesso valore in tutta la massa di gas, si raggiunge lo stato (punto A′) di equilibrio, da cui si può sempre tornare a quello iniziale A riducendo il volume di Δv e attendendo che la pressione aumenti ovunque di Δp: la trasformazione AA′ è reversibile (o invertibile) e lo è l’intera trasformazione AB se la si effettua con una serie di trasformazioni elementari infinitesime del tipo AA′, tali che la spezzata con cui, in fig. 1, si va da A a A′ e le analoghe spezzate successive tendano alla linea continua AB.
Le trasformazioni reversibili (successioni di infiniti stati di equilibrio infinitamente poco diversi l’uno dal precedente), il cui studio può essere semplice e immediato, sono processi ideali, che richiedono un intervallo di tempo infinito; le trasformazioni reali sono irreversibili (o non invertibili) poiché di durata finita. Si noti che l’avere luogo in modo infinitamente lento (quasi statico) è condizione necessaria ma non sufficiente per la reversibilità di una trasformazione. Importanti sono le trasformazioni cicliche, o chiuse (quelle non cicliche sono dette aperte), in cui stato iniziale e finale coincidono (➔ ciclo). Nel caso di trasformazioni reversibili di una massa di gas rappresentate nel piano di Clapeyron, il lavoro (➔) delle forze di pressione contro l’ambiente è pari all’integrale del lavoro infinitesimo pdv, cioè è misurato dall’area del rettangoloide in grigio di fig. 1:
Tale lavoro è assunto positivo se è fatto dal sistema contro l’ambiente, con aumento di volume. Se cambia la trasformazione con cui si passa dallo stato A allo stato B, cambia in genere il valore dell’integrale. Nel caso di trasformazioni cicliche, il lavoro,
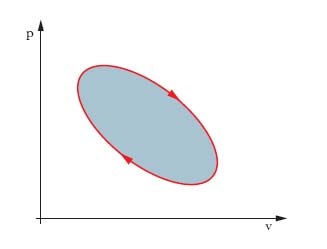
è misurato dall’area della superficie racchiusa dalla linea che rappresenta la trasformazione (area scura in fig. 2), e si considera positivo se la linea è percorsa in senso orario. Generalizzando al caso di un lavoro L qualunque, esso è pari alla circuitazione di i∙de, essendo i la grandezza intensiva, e la grandezza estensiva relative alle azioni da cui il lavoro deriva.
Importanti trasformazioni termodinamiche, soprattutto nel campo delle macchine termiche a fluido, sono quelle a temperatura costante (➔ isoterma), a pressione costante (➔ isobara), a volume costante (➔ isocora).
Principio zero della termodinamica
Due sistemi, ognuno in equilibrio termico con un terzo sistema, risulteranno in equilibrio termico tra di loro.
Primo principio della termodinamica
Questo principio, che stabilisce l’equivalenza tra calore e lavoro ed estende ai fenomeni termici il principio di conservazione dell’energia, afferma che il rapporto tra quantità di calore scambiata in una qualsiasi trasformazione ciclica e lavoro fatto nella stessa trasformazione è costante, indipendente dal ciclo eseguito, dalla natura dei corpi che partecipano alla trasformazione e dai dispositivi usati per effettuarla. In tal modo si stabilisce l’equivalenza tra calore e lavoro: gli effetti su un sistema di un dato lavoro si possono compensare (riportando il sistema allo stato iniziale) facendo scambiare al sistema una quantità di calore che è in rapporto definito e costante con il lavoro, o viceversa. Poiché le quantità di calore sono positive se assorbite dal sistema e negative se cedute, se lungo un ciclo è assorbito calore necessariamente del lavoro deve essere eseguito dal sistema sull’ambiente e viceversa. L’equivalenza si enuncia anche come reciproca convertibilità del calore in lavoro: se in un ciclo si trasforma calore in lavoro o viceversa, la conversione ha luogo secondo un rapporto definito e costante. Il valore di tale rapporto fornisce il numero di unità di lavoro corrispondente a un’unità di quantità di calore (equivalente meccanico del calore); il suo inverso, cioè il numero di unità di quantità di calore corrispondente a un’unità di lavoro è l’equivalente termico del lavoro. Assunti il joule come unità di lavoro e la caloria come unità di quantità di calore, l’equivalenza è di 4,186 J/cal e di 0,2389 cal/J; le quantità di calore si possono esprimere in unità di lavoro, per es. in joule, come si fa nel Sistema Internazionale (SI) di unità di misura. Per questo si parla del primo principio come di un principio di equivalenza. Nel caso di un ciclo, esprimendo calore e lavoro nelle stesse unità, si ha dunque Q=L o anche Q−L=0; descrivendo il ciclo in due fasi (da uno stato A a uno B e poi da B ad A), si ha che in una trasformazione aperta la quantità QAB−LAB, a differenza di QAB ed LAB presi individualmente, dipende solo dallo stato iniziale e finale e non dalla trasformazione considerata, cioè è esprimibile come variazione UB−UA di una funzione U dipendente solo dallo stato del sistema. Ciò si traduce nella relazione
che si riduce a
se la trasformazione è chiusa (A≡B) e alla relazione
per una trasformazione infinitesima. La funzione di stato U è detta energia interna del sistema poiché esprime la capacità del sistema a compiere lavoro in assenza di scambi di calore (dU=−δL, per δQ=0) o di scambiare calore in assenza di lavoro (dU=δQ, per δL=0). La relazione [5] è assunta come enunciato analitico del primo principio della t. e significa che mentre dU è un differenziale esatto, per cui è
δL=pdv, a norma della [2], non lo è, e così pure δQ (di qui il simbolo δ). L’energia interna U, come ogni altra grandezza di stato, è definita a meno di una costante additiva. La [5] si estende al caso di azioni elettriche, magnetiche ecc., includendo in δL i lavori elementari di queste azioni, e si interpreta come una estensione della conservazione dell’energia, introdotta in meccanica, al caso in cui intervengano anche scambi termici.
Secondo principio della termodinamica
Questo principio traduce il fatto che nei cicli si hanno limitazioni alla trasformazione di calore in lavoro (ma non a quella di lavoro in calore) e si esprime analiticamente nella forma
dove δQ è la quantità elementare di calore scambiata nel ciclo dal sistema con la sorgente a temperatura T (misurata con un termometro a gas perfetto e fissata la temperatura del punto triplo dell’acqua pari a 273,16). L’uguaglianza si ha solo in caso di cicli reversibili (per cui le T delle sorgenti coincidono con la temperatura del sistema in ogni fase del ciclo). Dalla [7] discende l’enunciato di Kelvin del secondo principio della t.: non è realizzabile un ciclo il cui unico risultato sia produrre lavoro a spese di calore prelevato da una sola sorgente; infatti, nel caso di ciclo con unica sorgente, per il primo principio si ha L=Q e per il secondo Q/T≤0, ovvero, essendo sempre T>0, Q≤0: non può quindi aversi L=Q>0. Dalla [7] discende anche l’enunciato di Clausius del secondo principio: non è realizzabile un ciclo il cui unico risultato sia far passare calore da un corpo freddo a uno caldo. Come applicazione del secondo principio, si consideri un sistema che in un ciclo scambia le quantità di calore Q1 e Q2 rispettivamente con le due (sole) sorgenti a T1 e T2, in modo che Ltot=Q1+Q2>0 (macchina termica motrice). Per soddisfare la disuguaglianza, almeno una delle quantità di calore deve essere positiva (assorbita dal sistema). La [7] in tal caso si scrive:
quindi se una quantità di calore è positiva, l’altra deve essere necessariamente negativa; sia per es. Q1>0 e quindi Q2<0. Le due disequazioni (in cui Q2, negativo, è sostituito da −|Q2|)
sono compatibili solo se T1>T2, cioè solo se si preleva calore dalla sorgente più calda e se ne cede alla più fredda. Ricordando che il rendimento è η=Ltot/Qassorbito), si ha
ma per la [9′] Q1/T1≤|Q2|/T2 ovvero T2/T1≤|Q2|/Q1 e quindi
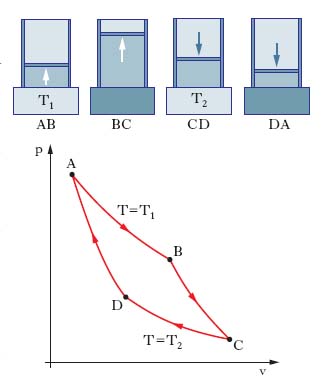
dove l’uguaglianza sussiste per ciclo reversibile. Poiché l’unico ciclo reversibile con due sole sorgenti è quello di Carnot (una espansione isoterma a T1, una espansione adiabatica fino a T2, una compressione isoterma a T2, una compressione adiabatica fino a T1, reversibili; fig. 3), si ha (teorema di Carnot)
cioè il rendimento di una macchina termica (che descrive un ciclo) di Carnot dipende solo dalle T delle sorgenti e non dal sistema termodinamico impiegato; il rendimento di una generica macchina termica a due sorgenti è sempre minore (al più uguale) di quello di una macchina di Carnot che operi tra le stesse sorgenti. Il teorema di Carnot si generalizza a macchine termiche che scambiano calore con più di due sorgenti: esse hanno η≤ηCarnot, con la macchina di Carnot operante tra due sorgenti aventi rispettivamente le T massima e minima.
Poiché in un ciclo di Carnot T1/T2=Q1/Q2, si può ridefinire operativamente la temperatura T sulla base della misurazione delle quantità di calore scambiate in un ciclo di Carnot operante tra la T da determinare e una di riferimento; la temperatura così definita, è detta temperatura termodinamica e coincide con quella misurata con un termometro a gas perfetto.
Dalla formulazione [7], poiché l’integrale tra due stati A e B non dipende dalla trasformazione reversibile, dipendendo solo da A e B, si può introdurre la funzione di stato S entropia (➔) definita a meno di una costante additiva arbitraria come
dove l’integrale da A a B è calcolato lungo una qualunque trasformazione reversibile. Dalla [7] discende inoltre che
o anche
dove l’uguaglianza vale per trasformazione reversibile: il confronto tra primo e secondo membro di queste disequazioni fornisce un criterio per definire le trasformazioni reversibili. Si noti che considerando un sistema termodinamico insieme all’ambiente con cui esso interagisce, si ottiene un sistema isolato e dalle [11], essendo nulla la quantità di calore da questo scambiata con l’esterno, si ha che l’entropia non varia in trasformazioni reversibili, mentre aumenta nelle irreversibili: l’affermazione che nelle trasformazioni reali, cioè irreversibili, l’entropia non può che aumentare è un altro enunciato del secondo principio. Considerando l’intero Universo, sistema isolato per eccellenza, si può dire, in termini cosmologici, che la sua entropia cresce in continuazione.
Terzo principio della termodinamica
La grandezza di stato entropia è definita a meno di una costante additiva; ciò comporta che mentre si può sempre calcolarne le variazioni, non si può viceversa determinare l’entropia di uno stato. Questa intrinseca indeterminazione è eliminata dal terzo principio della t. o principio di Nernst, per cui, per ogni trasformazione isoterma di un sistema termodinamico costituito da una sostanza pura allo stato solido cristallino è
Ciò implica l’irraggiungibilità dello zero assoluto (−273,15 °C), per cui si parla anche di principio dell’irraggiungibilità dello zero assoluto. La [12] stabilisce che al tendere della temperatura di un sistema allo zero assoluto, l’entropia tende al valore minimo che si assume, per comodità, pari a zero; perciò il terzo principio si esprime anche con l’enunciato di Planck per cui al diminuire indefinito della temperatura l’entropia tende al valore zero.
Funzioni termodinamiche
Con il nome di funzioni termodinamiche, o di potenziali termodinamici (➔ potenziale), si indicano alcune grandezze estensive in grado di dare, per derivazione, tutte le informazioni su un sistema termodinamico. Tra queste si hanno entropia, energia interna, entalpia, energia libera e entalpia libera. Le funzioni termodinamiche sono definite a meno di una costante arbitraria additiva il cui valore si può fissare attribuendo un dato valore (per es., zero) a ciascuna funzione in corrispondenza di uno stato standard o di riferimento.
L’energia interna, U, ricordando la definizione [5] e tenendo conto della [11″], si scrive anche, se il lavoro è solo quello delle forze di pressione e il sistema si descrive con due sole variabili di stato indipendenti (sistema termodinamico semplice):
sintesi analitica di primo e secondo principio. Così come si ha in meccanica per potenziale e componenti della forza, le derivate parziali della U rispetto alle variabili estensive danno grandezze intensive:
e perciò l’energia interna e grandezze che svolgono analogo ruolo sono dette potenziali termodinamici. A uno stato di equilibrio compete il minimo valore possibile per U. La funzione U è molto utile per studiare processi in cui restino costanti una o più variabili estensive (trasformazioni isoentropiche e isocore). L’equazione di stato del sistema si ottiene eliminando S fra le [14].
L’entalpia si definisce come
[15] H = U + pv,
e per un sistema semplice è
dove l’uguaglianza vale solo per trasformazioni reversibili. L’equazione di stato del sistema si ottiene eliminando H fra le due ultime relazioni. L’uso di H è molto utile nelle isobare nelle quali, se reversibili, l’aumento di entalpia è pari alla quantità di calore assorbito. All’equilibrio corrisponde il massimo valore possibile per H.
L’energia libera, introdotta da Helmholtz e perciò detta anche funzione (o energia libera) di Helmholtz, si definisce come
[17] A = U − TS,
e per un sistema semplice si ha
quest’ultima relazione è l’equazione di stato. All’equilibrio corrisponde il minimo valore possibile per A. Tale funzione è utile in particolare per le isoterme, per le quali, se reversibili, il lavoro fornito all’esterno uguaglia la diminuzione di A.
L’entalpia libera, introdotta da Gibbs e perciò detta funzione di Gibbs o anche energia libera di Gibbs, è definita come:
[19] G = H − TS,
dove l’entalpia gioca un ruolo analogo a quello dell’energia interna nella definizione dell’energia libera. Per un sistema semplice è
l’ultima di queste relazioni costituisce l’equazione di stato. All’equilibrio corrisponde il minimo valore possibile per G. L’entalpia libera è importante per i cambiamenti di stato, processi isobari e isotermi per i quali quindi G resta costante nei casi reversibili, mentre diminuisce nei casi irreversibili.
Notevole importanza pratica hanno le equazioni di Maxwell della t., ottenute uguagliando le derivate seconde miste delle funzioni termodinamiche. Per un sistema termodinamico semplice esse sono:
Mediante queste relazioni si possono esplicitare le funzioni termodinamiche di un sistema, note l’equazione di stato e la legge di dipendenza dalla temperatura del calore specifico a volume o a pressione costante.
Termodinamica dei processi irreversibili
Le leggi fondamentali della t. classica si riferiscono a fenomeni reversibili. I fenomeni reali, pur presentando irreversibilità per disuniformità spaziali e scostamenti dall’equilibrio, essendo queste modeste, si possono spesso studiare come reversibili, tenendo conto dell’irreversibilità mediante correzioni (per es., ciò accade per i cicli delle macchine termiche). In altri casi, le irreversibilità sono intrinseche al fenomeno, descrivibile solo trattando sistematicamente distribuzione spaziale ed evoluzione temporale dei parametri. La t. dei processi irreversibili si applica nei campi delle reazioni chimiche, della conduzione termica ed elettrica, dei moti dei fluidi viscosi, dei fenomeni acustici, dei fenomeni di rilassamento di varia origine.
Per i sistemi in cui le trasformazioni risultano irreversibili, avendosi variazioni spaziali e temporali dei parametri termodinamici, si introduce il concetto di valore locale. Esso è quello relativo a una porzione del sistema tale che, pur essendo ogni parametro termodinamicamente significativo, risulti ivi costante (analogamente per i valori istantanei). Si suppone poi (postulato dell’equilibrio locale) che le relazioni tra le grandezze locali siano le stesse che si avrebbero se, nell’intervallo di spazio e di tempo cui si riferiscono, il sistema fosse in equilibrio. Per una descrizione locale vanno poste in forma opportuna le leggi di conservazione della massa e i primi due principi della termodinamica. Se nel sistema coesistono n specie chimiche diverse e se si indica con Jk il flusso specifico di diffusione materiale, la conservazione della massa si esprime come
Il primo principio della t. come principio di conservazione dell’energia si esprime nella forma:
dove u è il valore locale dell’energia interna specifica, ρ la densità, Jq il flusso termico specifico, v il volume specifico, p la pressione, Ξ un termine legato a gradiente di velocità e tensore degli sforzi, t il tempo. Il secondo principio della t. stabilisce che nei processi irreversibili l’entropia totale aumenta e perciò per descriverli è importante l’intensità di sorgente entropica σ (entropia prodotta per unità di volume e di tempo associata a fenomeni dissipativi). Poiché i parametri termodinamici variano nel tempo e nello spazio, mentre l’entropia è definita solo per gli stati di equilibrio di un sistema, si ricorre al postulato dell’equilibrio locale, supponendo che il valore di S in ogni regione infinitesima si determini con le stesse relazioni fra parametri valide se nell’intervallo di tempo e di spazio considerato, il sistema fosse in equilibrio. Un processo irreversibile si descrive in base a un’equazione di bilancio per cui la variazione dS nel sistema durante il tempo dt è data dalla somma della variazione dSe, legata a scambi di materia e energia (attraverso la superficie A che separa sistema e ambiente) e la variazione dSi, dovuta a dissipazioni legate alle irreversibilità. Si ha:
[24] dS = dSe + dSi,
o, in forma esplicita:
dove s è l’entropia specifica (cioè dell’unità di volume), V il volume del sistema, Js il flusso esterno di entropia per unità di superficie e di tempo e l’integrale di superficie diviene di volume grazie al teorema di Gauss-Green:
Dalle [25] e [26] si ricava per σ:
Per un sistema aperto, Js è dovuto ai flussi Jk di energia e materia attraverso la superficie che separa sistema e ambiente secondo la
dove ogni Jk si riferisce alla grandezza Mk scambiata e le Xk sono le forze termodinamiche, o affinità, che promuovono i flussi Jk. Dalla [28] consegue che:
Essendo ds esprimibile come:
dove mk è il valore di Mk riferito all’unità di volume, per ciascuna Mk si può scrivere un’equazione analoga alla [27] ma priva del termine di produzione (per le Mk, a differenza dell’entropia, non vi è generazione interna dovuta a fenomeni dissipativi). L’equazione di bilancio diventa:
Combinando le [30] e [31], risulta:
Infine, dalle [27], [29] e [32], si ha:
[33] σ = ∑ grad Xk∙Jk,
k
da cui risulta che per ottenere il valore locale σ e dunque l’evoluzione temporale di un sistema sede di un processo irreversibile bisogna conoscere le relazioni fra flussi Jk e affinità Xk. Solo per alcuni fenomeni semplici esse sono relazioni lineari (per es., la legge di Fourier, la legge di Ohm, la legge di Fick), mentre nella maggior parte dei casi reali il problema è complesso; la soluzione è perciò approssimata in base a un’estensione di tali leggi (t. lineare dei processi irreversibili), che tiene conto anche delle azioni incrociate (influenza dell’affinità Xi sul modulo Jk del flusso); si pone cioè
[34] Jk = ∑ LkiXi.
i
Le [34] sono dette equazioni fenomenologiche e, pur valide per varie condizioni sperimentali, non lo sono in generale e vanno considerate come relazioni di prima approssimazione, corrispondenti al primo termine dello sviluppo in serie delle leggi effettive. I coefficienti Lki, detti coefficienti fenomenologici, dipendono dalla natura del corpo considerato e dallo stato locale e in genere si possono determinare sperimentalmente. Alcuni sono esprimibili mediante quelli, noti, di conduttività interna, resistività elettrica e diffusione. Inoltre talune relazioni generali legano fra loro i vari coefficienti Lki come la relazione di reciprocità di Onsager:
[35] Lki = Lik.
L’ipotesi di linearità per le relazioni tra flussi e affinità non è valida per es. in sistemi biologici e sistemi sede di reazioni chimiche. Al riguardo, di grande interesse è lo sviluppo della t. dei processi irreversibili dovuto a I. Prigogine e basato sull’analisi della stabilità dei sistemi termodinamici e sulla possibilità di formazione di configurazioni, dette strutture dissipative, sostenute dai flussi materiali ed energetici fra sistema e ambiente. Tale approccio si applica anche ai processi di disequilibrio non lineare frequenti in biologia, quali, nel funzionamento della cellula, il flusso di composti lungo le vie metaboliche, il trasporto attivo attraverso le membrane, i meccanismi di controllo dell’espressione genica nei batteri. Le esperienze compiute in passato sui sistemi non lineari di tipo fisico o chimico dimostravano come, al contrario che nei sistemi biologici, una condizione di forte disequilibrio si traduceva nel rapido raggiungimento di uno stato disordinato e non nella comparsa di strutture organizzate come quelle note per le cellule viventi (per es., sintesi di proteine e di DNA; aggregazione di fosfolipidi nella membrana cellulare). Prigogine risolse questa apparente contraddizione grazie al concetto di struttura dissipativa di cui fornì modelli sperimentali di laboratorio. Le strutture dissipative (➔ dissipazione) sono fenomeni, in particolare reazioni chimiche complesse, che, se avvengono in un sistema aperto lontano dall’equilibrio, in cui si ha scambio continuo di materia e di energia con l’esterno (tipico degli organismi viventi), mostrano la capacità del sistema di strutturarsi macroscopicamente mediante processi di autoorganizzazione dei propri costituenti in configurazioni di comportamento cooperativo (➔ sinergetica) con un aumento spontaneo di ordine in uno stato di forte disequilibrio.
Irreversibilità macroscopica e reversibilità microscopica
La t., per il secondo principio, è una teoria non simmetrica per inversione del tempo (➔): in un sistema isolato, anche solo termicamente, i processi che portano a un aumento dell’entropia totale si possono realizzare spontaneamente, mentre quelli ottenuti dai precedenti invertendo il verso di percorrenza del tempo, che comporterebbero una diminuzione di entropia totale, non sono permessi. Ciò pone il problema di come conciliare la t. con la meccanica statistica, fondata su teorie invarianti per inversione temporale, come la meccanica classica e quantistica. Anche l’esperienza quotidiana mostra l’intrinseca irreversibilità dei processi naturali. La ripresa cinematografica dell’accensione di un fiammifero, proiettata in senso inverso implica la sensazione di un evento impossibile (dalla cenere si riforma il fiammifero); se il filmato riguarda fenomeni elementari come le oscillazioni non smorzate di un pendolo non si nota alcuna ‘innaturalezza’ nella proiezione in senso inverso. Sembra quindi esistere una netta divisione tra due tipi di fenomeni. Da una parte si hanno le leggi di evoluzione che descrivono per es. la conduzione del calore e la diffusione, con una struttura intrinsecamente irreversibile, e il secondo principio della t., che stabilisce una definita direzionalità temporale (il calore non passa spontaneamente dal corpo più freddo a quello più caldo, le sostanze in soluzione diffondono da zone a maggiore concentrazione verso quelle a concentrazione minore); dall’altra, valgono le leggi fondamentali della meccanica, con una struttura reversibile. Le equazioni di Newton (per semplicità si considera solo il caso della meccanica classica) per un sistema di N particelle, di massa m1, m2, ..., mN, interagenti tra loro, sono mi(d2xi/dt2)=Fi(x1, ..., xN), essendo xi la posizione della i-ma particella con i=1, 2, ..., N. Si supponga di risolverle fino a un tempo t>0, a partire da una certa condizione iniziale sulle posizioni e le velocità, vi, (x1(0), ..., xN(0); v1(0), ..., vn(0)), cioè ‘si proietti il film in avanti’. Al tempo t si inverta il tempo, lasciando invariate le posizioni x1(t), ..., xN(t) e sostituendo le v1(t), ..., vN(t) con −v1(t), ..., −vN(t), e si risolvano di nuovo le equazioni (ciò è l’analogo matematico del proiettare il film all’indietro). Essendo le equazioni di Newton invarianti rispetto all’inversione temporale, evoluzione diretta e inversa sono entrambe possibili e indistinguibili: il sistema ripercorrerà all’indietro la sua storia e, dopo un tempo t, tornerà nella posizione iniziale ma con velocità invertite. Tutto ciò pone un problema se si accetta che i costituenti ultimi della materia siano atomi interagenti secondo la meccanica di Newton (la meccanica quantistica per molti aspetti è irrilevante per i problemi dell’irreversibilità). Il primo, e forse maggiore, contributo alla conciliazione tra irreversibilità macroscopica e reversibilità delle leggi di evoluzione a livello microscopico è dovuto a Boltzmann, con il suo teorema H. Per un sistema di molecole di gas, assimilabili a sferette elastiche, Boltzmann ricavò, con opportune ipotesi, la legge di evoluzione (detta equazione di Boltzmann) per la funzione di distribuzione f(x, v, t), cioè la densità di probabilità di trovare una molecola con velocità v nel punto x al tempo t e dimostrò il teorema H: la quantità H(t)=ʃf(x, v, t)lnf(x, v, t)dxdv diminuisce nel tempo e assume il suo valore minimo in corrispondenza della distribuzione di Maxwell-Boltzmann fMB(x, v) ∝ exp[−(v2/2mkT)], dove k è la costante di Boltzmann e T la temperatura termodinamica del gas. Poiché l’entropia è proporzionale a −H, si ha che l’entropia aumenta sempre ed è massima in corrispondenza della distribuzione di Maxwell-Boltzmann: il teorema H costituirebbe quindi una dimostrazione del secondo principio. E. Zermelo notò però che il teorema H è in disaccordo con il teorema della ricorrenza di Poincaré, per cui in ogni sistema meccanico, il cui moto avviene in una regione limitata dello spazio delle fasi, a un certo tempo finito TR il sistema ritorna vicino alle condizioni iniziali. Poiché la funzione di distribuzione f, e quindi H, dipendono da posizioni e velocità delle molecole, quando il sistema torna, al tempo TR, vicino al suo stato iniziale, anche H deve assumere un valore prossimo a quello iniziale. J. Loschmidt notò che se H diminuisce dal tempo 0 al tempo t, e al tempo t si invertono le velocità, allora a un tempo maggiore di t si deve avere un aumento di H, a causa della simmetria delle equazioni del moto sotto inversione del tempo. Il problema del teorema H non è nella derivazione matematica del risultato dH(t)/dt≤0, a partire dall’equazione di Boltzmann, bensì nel modo in cui quest’ultima è stata ottenuta, per cui un ruolo centrale è svolto dall’assunzione sulla probabilità di collisione tra due molecole con date velocità (ipotesi di caos molecolare, o Stosszahlansatz). Questa assunzione non si giustifica con pure considerazioni dinamiche ed è, di fatto, un postulato di natura probabilistica. Dunque l’equazione di Boltzmann, e il teorema H, vanno considerati validi non in modo assoluto, ma in quanto forniscono l’andamento più probabile: H(t) non decresce monotonamente, ma ha un’evoluzione molto irregolare che, in media, segue l’andamento previsto dal teorema H. Boltzmann, per quanto riguarda il paradosso della ricorrenza, notò come in 1 cm3 di gas, a pressione e temperatura normali, per tornare alla condizione iniziale, con una precisione di 10−9 m nelle posizioni e 1 m/s nelle velocità, bisogna aspettare un tempo dell’ordine di 101019 anni, enorme anche rispetto all’età dell’Universo. In semplici modelli probabilistici si può mostrare che l’intuizione di Boltzmann sulla correttezza dell’ipotesi di caos molecolare è giusta per scostamenti dall’equilibrio non grandi rispetto alle fluttuazioni spontanee tipiche. Per quanto riguarda il paradosso della reversibilità, esso si basa sul poter conoscere con precisione infinita, e quindi invertire, le velocità delle particelle a un dato istante. Se si introduce il concetto di preparazione del sistema in uno stato macroscopico, considerando l’insieme delle configurazioni microscopiche corrispondenti a un dato stato macroscopico, la validità del teorema H si riconduce al fatto che per stati macroscopici molto lontani dall’equilibrio le configurazioni che danno una riduzione di H sono molto più numerose di quelle che ne danno un aumento.
Sugli argomenti di Boltzmann non concorda tutta la comunità scientifica e sull’origine dell’irreversibilità coesistono oggi cinque classi di interpretazioni: a) l’irreversibilità nasce in sistemi aperti per cui una descrizione stocastica è più appropriata e priva di difficoltà tecniche; b) l’origine dell’irreversibilità è nel procedimento di misura, in particolare nella meccanica quantistica in cui si ha il collasso della funzione d’onda in seguito a un’osservazione; c) l’elemento essenziale per l’irreversibilità è l’altissimo numero di particelle coinvolte; d) l’irreversibilità nasce dal processo di media su piccole regioni spaziali e/o temporali, connesso alla definizione delle osservabili macroscopiche; e) alla base dell’irreversibilità vi è l’incertezza del dato iniziale.
Comunque, gli studi sul caos deterministico hanno mostrato la sostanziale correttezza delle idee di Boltzmann. Alla luce della forte dipendenza dalle condizioni iniziali, tipica dei sistemi dinamici caotici, si comprende come il paradosso della reversibilità sia in pratica irrilevante, a prescindere dal numero di gradi di libertà. Per un’inversione esatta delle velocità, il valore di H deve aumentare, se prima diminuiva; nel caso di inversione con un piccolo errore, la traiettoria del sistema invertito si allontana velocemente da quella teorica (quella invertita senza errore) e H cresce solo per un tempo molto breve, per poi diminuire di nuovo. Tutto ciò è evidente in esperimenti numerici all’elaboratore. Il paradosso della ricorrenza nei sistemi caotici richiede tempi che crescono esponenzialmente con il numero N di gradi di libertà: TR~CN con C>1, quindi anche con N non molto grande (per es., N=10-100) il tempo di ricorrenza TR è enorme, di fatto non osservabile. Si noti infine come nel problema della irreversibilità sia nascosto un problema di livelli di realtà, cioè di come si guarda a un fenomeno. Come osservato da P. Duhem, se fosse dato di scorgere le molecole di un fluido, si noterebbe un’agitazione tumultuosa sia in un flusso laminare, che a livello macroscopico appare regolare, sia in un flusso turbolento, il cui comportamento è irregolare anche a livello macroscopico. Ciò si comprende mediante un esperimento concettuale: versato del profumo in un angolo di una stanza, le sue molecole, all’inizio concentrate in una piccola regione, presto occuperanno tutta la stanza; se si immagina di ‘filmare’ le molecole e di far girare la pellicola all’indietro, si vedrà un fenomeno ‘innaturale’ per cui le molecole sparse si riuniscono in un angolo; il film al contrario apparirà invece normale guardando o una sola molecola (o due o tre) oppure tutte le molecole in una piccola zona della stanza.

![[1] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/50/FORMULE_termodinamica_01.jpg)
![[2] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/99/FORMULE_termodinamica_02.jpg)
![[3] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/7a/FORMULE_termodinamica_03.jpg)
![[4] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/78/FORMULE_termodinamica_04.jpg)
![[5] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/7b/FORMULE_termodinamica_05.jpg)
![[6] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/d/de/FORMULE_termodinamica_06.jpg)
![[7] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f1/FORMULE_termodinamica_07.jpg)
![[8] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/1/13/FORMULE_termodinamica_08.jpg)
![[9′] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/3e/FORMULE_termodinamica_09.jpg)
![[9″] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/a/a9/FORMULE_termodinamica_09B.jpg)
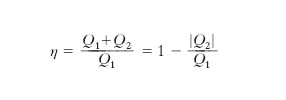
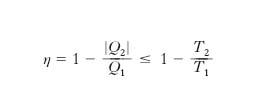
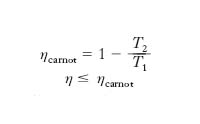
![[10] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/e/e5/FORMULE_termodinamica_10.jpg)
![[11′] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/4/4d/FORMULE_termodinamica_11.jpg)
![[11″] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/a/ae/FORMULE_termodinamica_11B.jpg)
![[12] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/8/88/FORMULE_termodinamica_12.jpg)
![[13] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/75/FORMULE_termodinamica_13.jpg)
![[16] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b3/FORMULE_termodinamica_15.jpg)
![[18] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b0/FORMULE_termodinamica_18.jpg)
![[20] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/56/FORMULE_termodinamica_20.jpg)
![[21] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/7c/FORMULE_termodinamica_21.jpg)
![[22] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/0/09/FORMULE_termodinamica_22.jpg)
![[23] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f4/FORMULE_termodinamica_23.jpg)
![[25] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/ff/FORMULE_termodinamica_24.jpg)
![[26] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/32/FORMULE_termodinamica_26.jpg)
![[27] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/a/a4/FORMULE_termodinamica_27.jpg)
![[28] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/96/FORMULE_termodinamica_28.jpg)
![[29] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/0/03/FORMULE_termodinamica_29.jpg)
![[30] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f7/FORMULE_termodinamica_30.jpg)
![[31] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/8/82/FORMULE_termodinamica_31.jpg)
![[32] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/33/FORMULE_termodinamica_32.jpg)