simmetria

simmetria Distribuzione ordinata delle parti di un oggetto tale che si possa individuare un elemento geometrico (un punto, una linea, una superficie) rispetto al quale a ogni punto dell’oggetto posto da una parte di esso corrisponda, a uguale distanza, un punto dall’altra parte. Con significato più generico, disposizione uniforme, invariante, di elementi di un assetto o di un sistema.

Biologia

fig. 1

fig. 2

fig. 3

fig. 4

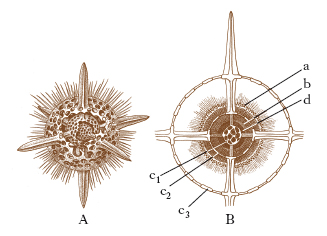
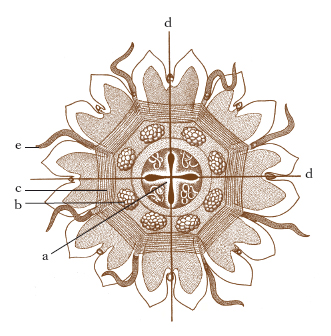
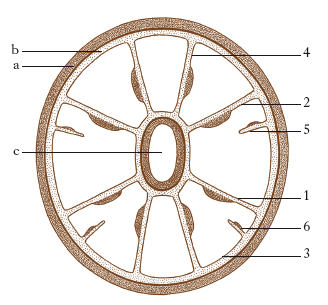
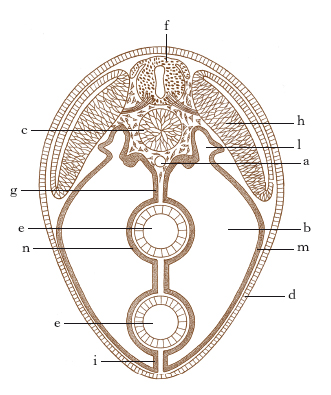
Modello geometrico cui fa riferimento il corpo degli organismi, basandosi su sistemi coordinati di assi e di piani. Nella simmetria sferica tutti i diametri della sfera sono assi di simmetria, e tutti i piani passanti per il centro sono piani di simmetria, che dividono il corpo in due metà simmetriche: l’esempio tipico è quello dei Radiolari (fig. 1). La simmetria radiale o raggiata (detta anche ciclomeria) è simile a quella di una ruota a raggi; esiste un asse principale, l’asse della ruota per lo più a poli non equivalenti, e tutti i piani che passano per esso, pur distinti in principali (d in fig. 2) e secondari, sono piani di simmetria: esempio tipico quello dei Celenterati, in particolare delle Meduse. La simmetria biradiale o biradiata (fig. 3) è una simmetria raggiata in cui due soli dei piani passanti per l’asse principale dividono il corpo simmetricamente, com’è il caso degli Antozoi. La simmetria bilaterale (fig. 4), tipica dei Metazoi, è associata a fenomeni di cefalizzazione ed è determinata da un solo piano che passa per l’asse principale del corpo, sempre eteropolare, cioè a poli non equivalenti: quest’unico piano di simmetria si chiama anche mediano o sagittale; i piani paralleli a esso si chiamano mediali o parasagittali; i piani perpendicolari a esso in senso antero-posteriore, frontali; in senso dorso-ventrale, trasversali.

Negli organismi vegetali, si distingue una simmetria raggiata (o multipolare, o polisimmetrica) caratteristica di vegetali unicellulari, di colonie e anche di organi vegetali conici (radici) o cilindrici (cauli), nei quali tutti i piani contenenti l’asse longitudinale sono piani di simmetria (organismi e organi actinomorfi); la simmetria bilaterale doppia è quella in cui gli organi presentano due piani di simmetria fra di loro ortogonali e di valore differente (organi bisimmetrici: pale del fico d’India); si ha simmetria bilaterale (o dorsoventrale o monosimmetrica o zigomorfa), quando il piano di simmetria è unico, cosicché l’organo o l’organismo è simmetrico solo sul lato destro e sinistro, o sul lato superiore e inferiore (organismi e organi zigomorfi: lamine fogliari, rami di abete). Se non si ha nessun piano di simmetria, gli organi sono detti asimmetrici (foglie di olmi, di begonie e fiori di valeriana).

Chimica

Per la determinazione della simmetria delle molecole si usano le stesse operazioni di simmetria adoperate per i cristalli. Nell’analizzare gli elementi di simmetria posseduti da una molecola, bisogna comunque tener conto della simmetria fisica, per la quale le operazioni devono portare alla sovrapposizione di atomi uguali; ciò comporta una diminuzione degli elementi di simmetria rispetto alla simmetria geometrica.

Il numero di simmetria (σ) di una molecola indica il numero complessivo di orientamenti indistinguibili che la molecola può assumere per rotazione completa attorno agli assi di simmetria rotazionale.

Fisica

Si indica con il termine simmetria l’invarianza rispetto a una trasformazione, intesa come proprietà sia di singole configurazioni o stati di un sistema sia delle relazioni tra di essi, cioè delle leggi che regolano il sistema; in questo secondo caso, una simmetria è associata a una trasformazione invertibile che lascia invariati l’insieme degli stati possibili di un sistema fisico e le sue leggi; in quest’ambito, i due termini simmetria e invarianza sono pertanto usati con lo stesso significato. Le trasformazioni di simmetria sono associate in maniera naturale a un gruppo di simmetria, in quanto la sequenza di due trasformazioni di simmetria è ancora una trasformazione di simmetria, la trasformazione identica è una simmetria, come anche la trasformazione inversa di una data. Il concetto di simmetria ha carattere generale e si applica a sistemi classici o quantistici, con numero finito o infinito di gradi di libertà. In particolare, in meccanica quantistica una simmetria, per le definizioni date sopra, deve trasformare lo spazio di Hilbert degli stati di un sistema in sé stesso, lasciando invariate le probabilità di transizione tra gli stati, cioè i moduli quadrati dei prodotti scalari fra i vettori di stato normalizzati (➔ meccanica).

Simmetrie continue

Una simmetria continua è caratterizzata da trasformazioni dipendenti da parametri che assumono valori continui. In una teoria di campo l’invarianza sotto simmetrie continue, per il teorema di Noether, implica che, in corrispondenza a ogni trasformazione infinitesima indipendente (individuata dall’indice a=1, ..., N essendo N il numero di parametri del gruppo di simmetria), esiste una quadricorrente Jμa (x, t) (dove μ è un indice spazio-temporale che assume i valori 1,2,3,4) che è conservata, ∑μδJμa/δxμ=0,e una carica QaʃJμa(x, t)dx, che non dipende dal tempo; nella teoria quantistica le Qa, dette anche generatori delle trasformazioni, sono operatori che determinano l’azione del gruppo di simmetria sullo spazio degli stati del sistema e obbediscono alle seguenti regole di commutazione:

[1] formula

dove i è l’unità immaginaria e le fabc sono le costanti di struttura del gruppo di simmetria. Le simmetrie continue di cui tutte le interazioni fondamentali godono sono quelle rispetto alle trasformazioni di Poincaré proprie, che implicano, tra l’altro, la conservazione del quadrimpulso e del momento angolare, e quelle rispetto alle trasformazioni di fase, o di gauge (➔), globali (cioè indipendenti dal punto dello spazio-tempo) dei campi che portano carica elettrica, numero barionico, numero leptonico; a esse sono associate, rispettivamente, la conservazione della carica elettrica, del numero barionico e dei numeri leptonici relativi alle tre famiglie di leptoni osservate. Queste ultime simmetrie sono l’esempio più semplice delle cosiddette simmetrie interne, cioè relative a trasformazioni coinvolgenti solo gradi di libertà (in questo caso carica elettrica, barionica, leptonica) non legati alla geometria dello spazio-tempo e detti essi stessi interni, e delle cosiddette simmetrie unitarie, cioè relative a trasformazioni che costituiscono un gruppo unitario (in questo caso a ognuna delle simmetrie è associato il gruppo unitario in una dimensione U(1)). Tutte le interazioni fondamentali, inoltre, risultano descritte da teorie di campo dotate di simmetria di gauge locale, cioè tale che le trasformazioni di invarianza possono essere scelte in modo indipendente in ogni punto dello spazio-tempo: la teoria della gravitazione (➔) è invariante per trasformazioni locali delle coordinate dello spazio-tempo, le interazioni elettromagnetiche e deboli risultano invarianti per trasformazioni locali su variabili interne associate al gruppo SU(2)×U(1), quelle forti al gruppo SU(3) detto di colore (➔ particelle elementari).

Supersimmetrie

Teoremi generali escludono che una teoria relativisticamente invariante ammetta gruppi di simmetria continui coinvolgenti, in modo non banale, trasformazioni su variabili spazio-temporali e interne; l’unica eccezione possibile consiste nel considerare, accanto a cariche di tipo bosonico, cioè soddisfacenti a regole di commutazione come le [1], anche cariche di tipo fermionico, cioè caratterizzate da regole di anticommutazione (analogamente a quanto si ha per i campi quantistici che descrivono particelle di spin semintero); queste simmetrie, dette supersimmetrie, classificano bosoni e fermioni in uno stesso multipletto e sono quindi le uniche simmetrie che implicano degenerazione nella massa di bosoni e fermioni. La supersimmetria, oltre a spiegare perché in natura si osservano sia bosoni, sia fermioni, potrebbe permettere di collegare le particelle di spin 1, associate alle forze, con quelle di spin 1/2, associate alla materia. Sono anche possibili schemi più generalizzati (supersimmetria estesa), in cui la supersimmetria lega tra loro particelle di spin 2 con particelle di spin inferiore, fino a 1, 1/2 oppure 0, fornendo la base per una teoria che potrebbe unificare la gravità, mediata dal gravitone di spin 2, con le altre interazioni. Una conseguenza notevole della relazione tra bosoni e fermioni caratteristica delle teorie supersimmetriche è, infine, la possibilità di costruire teorie di gauge supersimmetriche, in cui le divergenze ultraviolette (cioè dovute agli alti valori degli impulsi su cui si integra, nel calcolo dei termini dello sviluppo perturbativo di una teoria di campo quantistica) sono completamente assenti. Nonostante tutte queste proprietà interessanti, non esistono per ora prove sperimentali che la supersimmetria si applichi alle interazioni osservate. Anzi, lo studio delle teorie supersimmetriche delle interazioni elettrodeboli porta alla conclusione che nessuna delle particelle osservate di spin 1 ha come controparte supersimmetrica i quark o i leptoni osservati. Se la natura è, almeno parzialmente, supersimmetrica, ognuna delle particelle conosciute deve avere per compagno un’altra particella più pesante, non ancora osservata.

Geologia

In cristallografia, si definisce simmetria il ripetersi periodico di alcuni elementi di un cristallo (facce, vertici, spigoli), che rende possibile il loro ricoprimento un certo numero di volte, per rotazione intorno a un asse (asse di simmetria), per riflessione rispetto a un piano (piano di simmetria), per inversione rispetto a un punto (centro di simmetria); l’asse, il piano, il centro di simmetria costituiscono nel loro insieme gli elementi di simmetria.

È detta simmetria semplice quella generata di volta in volta da un elemento di simmetria; simmetria composta quella generata dalla combinazione di elementi di simmetria semplice (per es., l’asse giroide comporta una rotazione più una riflessione). Si chiama classe di simmetria l’insieme dei cristalli che presentano il medesimo grado di simmetria, cioè la stessa combinazione di elementi di simmetria: per es., appartengono alla stessa classe (monoclina prismatica) i cristalli di ortoclasio, gesso ecc., che presentano un asse binario, un centro e un piano di simmetria. Esistono soltanto 32 classi di simmetria possibili (suddivise in sette gruppi di ordine superiore o sistemi cristallini): tali classi sono contraddistinte da una duplice denominazione (per es., classe esacisottaedrica o della fluorite, classe esacistetraedrica o della blenda), di cui una relativa alla forma semplice caratteristica risultante dall’insieme delle facce equivalenti a una faccia data, la quale tagli i tre assi cristallografici a tre distanze diverse e finite, l’altra invece relativa al nome di un importante minerale appartenente alla classe stessa (➔ cristallo).

Matematica

In geometria, le simmetrie sono particolari tipi di trasformazione del piano in sé, o dello spazio in sé (o, più in generale, di uno spazio a n dimensioni in sé), che lasciano inalterate le distanze.

Simmetria centrale (o rispetto a un punto O, detto centro di simmetria)

La trasformazione che a ogni punto P associa il punto P′ tale che O sia il punto medio del segmento PP′.

Simmetria assiale (o rispetto a una retta r, detta asse di simmetria)

La trasformazione che a ogni punto P associa il punto P′ tale che r sia l’asse del segmento PP′.

Simmetria speculare (o rispetto a un piano α detto piano di simmetria)

La trasformazione che a ogni punto P associa il punto P′ tale che α sia perpendicolare al segmento PP′ nel suo punto medio.

Centro, asse, piano di simmetria di una figura F (detti anche genericamente elementi di simmetria di F) sono un punto, una retta, un piano tali che la corrispondente simmetria trasforma F in sé stessa; con significato più generale, una retta è detta asse di simmetria ternaria (o senaria ecc.) di un solido, se, nella rotazione di un angolo giro attorno a quella retta, il solido assume 3 (o 6 ecc.) volte la posizione iniziale (un asse di simmetria nel significato precedente è dunque un asse di simmetria binaria).

Simmetria obliqua (rispetto a una retta r o a un piano α)

Trasformazione analoga a quella definita inizialmente (che, per contrapposizione, viene talvolta detta ortogonale), ma in cui il segmento PP′ incontra r (o α) secondo un prefissato angolo (non retto). Si parla, in particolare, di simmetria radiale, per punti del piano tutti equidistanti dal centro di simmetria, oppure, per punti dello spazio, tutti equidistanti dall’asse di simmetria. Gruppo di simmetria di una figura F è il gruppo, per solito non abeliano, costituito da tutti i movimenti, diretti o inversi, che lasciano invariata F. Per es., il gruppo di simmetria di un triangolo equilatero è costituito dall’identità, dalle simmetrie rispetto a ciascuna delle tre mediane e dalle rotazioni di 120° e di 240° attorno al centro del triangolo.

Psicologia

Nella psicologia del comportamento, simmetria qualifica il tipo di rapporto interpersonale nel quale entrambi i soggetti tendono a esercitare un dominio sull’altro, instaurando una situazione di costante competitività, da cui può scaturire un equilibrio di tipo simmetrico. Si usa in contrapposizione a complementarità.