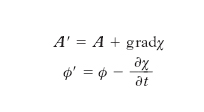gauge

gauge In inglese, misura, calibrazione. Il termine viene usato per indicare una particolare scelta o convenzione in base alla quale determinati enti acquistano certe proprietà. Trasformazioni di g. Nella teoria dell’elettromagnetismo, il potenziale vettore A e il potenziale scalare ϕ sono correlati al campo elettrico E e al vettore induzione magnetica B dalle relazioni E=−grad ϕ−∂A/∂t, B=rotA; queste relazioni non definiscono però in modo univoco i potenziali. Eseguendo infatti la trasformazione di g.:

dove χ (funzione di g.) è una funzione arbitraria dello spazio e del tempo, i vettori E e B (che sono le grandezze fondamentali del campo elettromagnetico direttamente osservabili) non cambiano. Generalmente si sceglie la funzione di g. in modo tale che sia divA=−(1/c²)∂ϕ/∂t (condizione o g. di Lorentz); in particolare nei casi stazionari deve essere divA=0 (condizione o g. di Coulomb). Le trasformazioni di g. hanno trovato larga applicazione nella teoria quantistica dei campi.

Sono dette teorie di g. quelle teorie le cui equazioni sono invarianti per trasformazioni di gauge. La più antica teoria di g. è la teoria del campo elettromagnetico; il campo elettrico e magnetico, e quindi le equazioni di J.C. Maxwell, rimangono infatti invariati se si modificano tutti i potenziali mediante una trasformazione di gauge. L’invarianza rispetto alle trasformazioni di g. (invarianza di g.) sussiste anche in elettrodinamica quantistica quando si considera l’interazione del campo elettromagnetico con una particella carica (per es., con un elettrone), purché si modifichi la fase della funzione d’onda della particella carica di una quantità proporzionale alla funzione di g. corrispondente; poiché, in generale, la modifica della fase risulterà diversa da punto a punto dello spazio-tempo, risultando tale la funzione di g., si dice anche che la teoria presenta una simmetria locale o che è invariante per trasformazioni locali (una modifica della fase indipendente dal punto corrisponde invece a una trasformazione globale o a numero finito di parametri). Come regola generale, l’invarianza di g. comporta l’esistenza di un campo vettoriale, il campo di gauge. L’invarianza delle leggi della fisica rispetto alle trasformazioni di g. (come anche alle trasformazioni dipendenti da un numero finito di parametri) ha una grande importanza perché impone restrizioni alla forma delle leggi fisiche stesse.

Le trasformazioni di g. dell’elettromagnetismo sono state estese da C.N. Yang e R. Mills alle rotazioni nello spazio dello spin isotopico nel caso dei nucleoni. Successivamente lo studio delle teorie di g. ha avuto grande importanza per la formulazione di una teoria unificata delle interazioni deboli ed elettromagnetiche. Le teorie di campo le cui equazioni risultano invarianti sotto il gruppo delle trasformazioni di g. sono a fondamento della moderna fisica delle particelle elementari; infatti, il Modello Standard, che descrive in modo fenomenologicamente soddisfacente le interazioni elettrodeboli (➔ deboli, interazioni) e forti (➔ forti, interazioni), è costituito da due teorie di g. fuse insieme in modo molto naturale.

In fisica delle particelle elementari, è detta gaugino ogni ipotetica particella di spin 1/2 (in unità della costante di Planck razionalizzata), che sia partner supersimmetrica di un bosone di g. (➔ supersimmetria).