forti, interazioni

In fisica delle particelle elementari, una delle 4 classi di interazioni fondamentali (f., elettromagnetiche, deboli e gravitazionali) alle quali si possono ricondurre, a livello microscopico, tutti i fenomeni fisici osservati. Derivano il nome dall’intensità relativamente elevata delle forze corrispondenti. A esse si deve in particolare la coesione dei nuclei atomici, in quanto le forze attrattive f. tra i nucleoni (neutroni e protoni del nucleo) prevalgono sulle forze repulsive elettromagnetiche dovute alle cariche positive dei protoni. Un dominio di applicazione particolarmente importante delle interazioni f. è costituito in effetti dalle forze nucleari. D’altra parte lo studio delle leggi fondamentali delle interazioni f. si svolge nell’ambito della fisica subnucleare, anche se non tutte le particelle subnucleari sono soggette alle interazioni forti. Le particelle che interagiscono fortemente sono dette adroni. Non hanno interazioni f. e quindi non sono adroni l’elettrone, il neutrino e gli altri leptoni, il fotone e i bosoni intermedi W^± e Z⁰ delle interazioni deboli.

Suddivisioni degli adroni

Gli adroni si dividono in barioni e mesoni a seconda che il loro spin sia, rispettivamente, semintero o intero in unità di ħ. Quindi il barione è un fermione e il mesone è un bosone . La cosiddetta spettroscopia degli adroni è molto vasta e articolata: oltre al protone e al neutrone si conoscono centinaia di particelle adroniche. La maggior parte di queste sono altamente instabili, con vite medie dell’ordine di 10⁻²²-10⁻²⁴ s. Questa elevata velocità di decadimento è una manifestazione della grande intensità delle interazioni forti. Alcuni adroni hanno vita media generalmente più lunga (e sono detti adroni quasi stabili): fra questi, i mesoni π^±, π⁰ (pioni), K^±, K⁰, K̅̅⁰ (kaoni), η ecc.; i barioni n (neutrone), Σ^±, Σ⁰, Λ, Ξ⁰, Ξ^--, Ω⁻ (iperoni) ecc. Il protone (p) è addirittura stabile (o almeno la sua vita media è maggiore di circa 10³² anni). La relativa lunghezza della vita media di tali adroni dipende dal fatto che essi non possono decadere mediante le interazioni f. a causa di leggi di conservazione che sono valide per le interazioni f. e non per le interazioni elettromagnetiche o per le interazioni deboli. La minore intensità di queste altre interazioni rende assai più lento il processo di decadimento.

Leggi di conservazione

Tutti i barioni posseggono una carica additiva conservata da ognuna delle interazioni conosciute, opposta per barioni e antibarioni, che prende il nome di numero barionico. La stabilità del protone è dovuta al fatto che esso è il più leggero dei barioni e quindi il decadimento del protone potrebbe solo avvenire con violazione del numero barionico (in quanto la conservazione dell’energia impone che la somma delle masse dei prodotti di decadimento sia minore della massa della particella che decade). Le interazioni f. rispettano inoltre la conservazione della parità P e della coniugazione di carica C come pure dei numeri quantici di spin isotopico, della stranezza, del charm ecc. Gli adroni più leggeri fra quelli dotati di tali numeri quantici possono solo decadere o tramite interazioni elettromagnetiche, che violano la conservazione dello spin isotopico, oppure tramite interazioni deboli che possono violare la conservazione dello spin isotopico, della stranezza, del charm ecc. Le leggi di conservazione già menzionate (che sono esattamente valide per le interazioni f.) e altre di validità approssimata (simmetrie unitarie SU(3), SU(6)), permettono una organizzazione della complessità dei livelli adronici. Infatti, tali simmetrie delle interazioni f. si riflettono sulla struttura degli stati adronici che si possono raggruppare in multipletti di adroni con masse approssimativamente uguali e con numeri quantici strettamente collegati.

Quark e loro cariche

Dallo studio sistematico di questi multipletti adronici, negli anni 1960 è emerso il risultato, di fondamentale importanza per il successivo sviluppo della fisica delle particelle elementari, che gli adroni sono stati legati di costituenti più semplici, di spin 1/2, detti quark (➔). I barioni sono composti da tre quark e i mesoni di una coppia quark-antiquark. Questa scoperta, inizialmente fondata sui dati della spettroscopia dei livelli adronici, è stata confermata da evidenze sperimentali completamente indipendenti. Quindi, il problema della formulazione di una teoria delle interazioni f. si è spostato dall’ambito degli adroni a quello, più fondamentale, dei quark. I quark sono dotati di diversi tipi di cariche che contribuiscono a determinare le loro varie interazioni. In particolare, i quark, a differenza degli adroni ordinari che ne sono privi, posseggono delle cariche forti, assolutamente conservate, che prendono il nome di cariche di colore. Precisamente ogni tipo di quark esiste in tre colori diversi. Il termine colore ha un valore puramente analogico e rappresentativo, in quanto le cariche forti non hanno niente in comune con i fenomeni ottici. Le interazioni f. tra i quark avvengono per scambio di gluoni (dall’ingl. glue, «colla»), particelle di spin 1 e massa nulla, soggette alle sole i. forti. I gluoni sono analoghi ai fotoni, che mediano le interazioni elettromagnetiche, ma a differenza dei fotoni che sono elettricamente neutri, i gluoni sono essi stessi colorati e ne esistono di otto diversi colori. Questo fatto rende la teoria delle interazioni f. basata sul colore, detta cromodinamica quantistica (QCD, quantum cromo-dynamics), assai più complicata dal punto di vista dinamico che non l’elettrodinamica quantistica (➔ elettrodinamica), con la quale ha peraltro in comune la struttura che deriva da un tipo particolarmente restrittivo di simmetria che prende il nome di invarianza di gauge (➔).

Confinamento e libertà asintotica

Il cosiddetto confinamento è il fenomeno qualitativamente più rilevante, che sembra risultare dalla complessa dinamica dei quark e dei gluoni colorati. Il confinamento consiste nel fatto che solo le particelle prive di colore sono osservabili come stati liberi. Come già accennato, tutti gli adroni osservati sono infatti neutri per quanto riguarda il colore. I quark e i gluoni non si osservano liberi, ma solo confinati all’interno degli adroni, oppure attraverso i getti di adroni (jets) ai quali danno luogo una volta prodotti nelle interazioni adroniche ad alte energie. Pertanto, a differenza delle molecole, degli atomi, dei nuclei, che sono stati legati di costituenti che possono essere liberati rompendo il legame e osservati separatamente come particelle libere, gli adroni non possono essere risolti nei loro costituenti in quanto le forze attrattive tra i quark aumentano con la distanza, cosicché il processo di liberazione di un quark è fisicamente irrealizzabile. D’altra parte, sussiste un’altra proprietà notevole della cromodinamica quantistica che prende il nome di libertà asintotica e riguarda l’andamento dell’intensità delle interazioni f. a piccole distanze. Mentre le interazioni tra particelle colorate divengono sempre più intense a grandi distanze e causano il confinamento, d’altra parte esse tendono a spegnersi a piccole distanze. Quindi, utilizzando acceleratori che permettono di produrre particelle-sonda così energetiche da potere esplorare il contenuto di un nucleone, si possono osservare i quark che si muovono praticamente liberi e puntiformi all’interno del nucleone stesso. Infine, riconsiderando alla luce della cromodinamica quantistica le forze nucleari, esse appaiono come forze derivate e complicate che si esercitano tra composti neutri rispetto al colore e che possono, di conseguenza, solo interagire tra loro per scambio di altri composti ugualmente neutri, cioè altri adroni per lo più leggeri, in particolare pioni e altri mesoni. Questa necessità di scambiare particelle di massa non nulla permette di spiegare il fatto che le forze nucleari si smorzano molto rapidamente (esponenzialmente) con la distanza, di modo che risultano trascurabili fra i nuclei di due atomi anche a stretto contatto tra loro (per es., in una molecola), in quanto le dimensioni di un atomo (~10^–8 cm) sono molto maggiori di quelle del nucleo (~10^–13 cm). Il raggio limitato delle forze nucleari fa sì che tutte le proprietà chimico-fisiche degli aggregati materiali siano determinate esclusivamente dalle interazioni elettromagnetiche tra gli elettroni atomici.

Spin isotopico

La nozione di simmetria delle interazioni f. per trasformazioni di spin isotopico o spin isobarico o isospin fu introdotta sulla base delle proprietà osservate dei nuclei (➔ isotopi). Tutte le differenze fra protoni e neutroni per quanto riguarda la struttura e i processi nucleari possono essere attribuite o alle interazioni elettromagnetiche, ovviamente diverse per le due particelle, perché il protone è elettricamente carico mentre il neutrone è neutro, o anche alle interazioni deboli. Il fatto che le interazioni f. non distinguono i protoni dai neutroni comporta l’invarianza delle interazioni f. per rotazioni nello spazio astratto dell’isospin, che trasformano uno stato di protone in uno di neutrone o in una sovrapposizione quantistica dei due. In completa identità con il formalismo valido per una particella di spin 1/2, i nucleoni sono detti formare un doppietto di isospin I=1/2 con componenti z, rispettivamente, I_z=+1/2 per il protone e I_z=−1/2 per il neutrone (la convenzione opposta essendo anche in uso). Anche per l’isospin si hanno multipletti di nuclei oppure di adroni di isospin I, formati da 2I+1 componenti, con I positivo intero o semintero. In tab. sono riportati i multipletti di isospin dei mesoni e dei barioni quasi stabili più leggeri. Vi si osserva che particelle di un dato multipletto hanno masse diverse fra loro, anche se le differenze di massa sono molto minori della massa media del multipletto stesso e della differenza fra questa e la massa media degli altri multipletti. Ciò indica che la simmetria di isospin non è esatta, ma le violazioni della simmetria sono molto piccole. Ciò è stato a lungo interpretato come un riflesso del fatto che le interazioni f. che rispettano la simmetria sono assai più intense delle interazioni elettromagnetiche e deboli che la violano. In realtà, la simmetria di isospin è dovuta al fatto che le interazioni f. sono identiche per tutti i sapori di quark e le masse dei quark u e d sono quasi uguali. Infatti, come si vede dalla tab., gli adroni in un dato multipletto di isospin differiscono tra loro per il contenuto in quark u e d.

Stranezza e ipercarica

La stranezza fu introdotta alla fine degli anni 1950 per spiegare le proprietà fino ad allora misteriose di talune particelle (i kaoni, gli iperoni) scoperte in quegli anni, che per il loro comportamento meritarono il nome di particelle strane. Le particelle strane sono prodotte con elevate sezioni d’urto (quindi con elevata velocità di reazione), dovute alle i. forti. D’altra parte, decadono molto lentamente, con le vite medie delle particelle a decadimento dovuto alle interazioni deboli. La soluzione del problema, cioè la ragione per la quale i decadimenti non avvengono mediante le interazioni f., sta nel fatto che tali particelle posseggono un nuovo tipo di carica, al quale fu appunto dato il nome di stranezza, che è conservata dalle interazioni f. ed elettromagnetiche ma non dalle interazioni deboli. Nei processi di produzione dovuti alle interazioni f. le particelle strane sono prodotte in coppie di stranezza opposta (produzione associata). Una volta prodotta, una particella strana leggera può solo decadere mediante le interazioni deboli, che permettono la transizione a uno stato finale di stranezza nulla. Una quantità importante legata alla stranezza è la ipercarica definita come Y=B+S, dove B è il numero barionico e S è la stranezza. L’importanza dell’ipercarica sta nella relazione con la carica elettrica Q (in unità della carica del protone). Per particelle senza charm e altri sapori pesanti vale infatti la relazione di Gell-Mann e Nishijima, Q=I_z+(Y/2) dove I_z è la componente z dell’isospin. Oggi sappiamo che la stranezza è un particolare tipo o flavour (sapore) di quark. Il quark s, più pesante dei quark u e d, ha stranezza S=−1 e il corrispondente antiquark s̄ ha S=+1. Pertanto la stranezza di un adrone è S=n_s̄−n_s, cioè il numero di s̄ meno il numero di s tra i quark e antiquark componenti.

Flavour pesanti

fig. 1

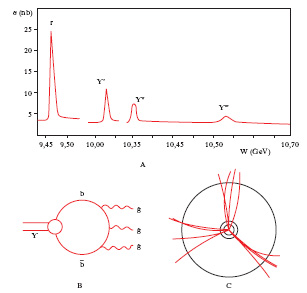
Del tutto analoghi alla stranezza sono il charm e gli altri flavour pesanti. Oltre ai quark leggeri già menzionati esistono anche il quark c (charm) scoperto nel 1974, con massa intorno a 1,5 GeV/c², il quark b (bottom o beauty) scoperto nel 1977, con massa di circa 4,5 GeV/c², e il quark t (top o truth), scoperto nel 1995, con massa di circa 175 GeV/c². Gli adroni più leggeri dotati di charm per primi identificati e studiati (i mesoni D⁺ ~ cd̅, D⁰ ~ cū, F⁺ ~ cs̄ e il barione Λ⁺_c ~ cud) decadono mediante le interazioni deboli con vite medie comprese tra 10^–13 e 10^–12 s. Meno avanzata è la conoscenza sperimentale degli adroni con beauty, ma i corrispondenti decadimenti deboli paiono avere vite medie dell’ordine di 10^–12 s. Esistono poi mesoni con charm o beauty nascosto ( quarkonio, fig. 1), come le particelle di spin 1, J/Ψ ~ cc̄ e Ƴ ~ bb̅ che hanno determinato la scoperta del c e del b rispettivamente. Questi stati decadono mediante le interazioni f. e le interazioni elettromagnetiche con velocità comparabili, in quanto le interazioni f. sono soppresse dalla cosiddetta regola di Zweig. Questa stabilisce che le probabilità di creazione o di distruzione di una coppia di quark-antiquark pesanti è piccola. Poiché non è energeticamente possibile il decadimento in adroni con charm (beauty) la coppia quark-antiquark presente nello stato iniziale deve annichilarsi in adroni attraverso uno stato intermedio di gluoni. Dato che i quark sono pesanti la probabilità di annichilazione è piccola in quanto la cromodinamica quantistica è asintoticamente libera, cioè le interazioni f. tra quark e gluoni si attenuano quando il trasferimento di energia-impulso è grande. Gli stati mesonici composti da una coppia di quark-antiquark pesanti dello stesso tipo o sapore hanno proprietà tanto più spettacolari e interessanti quanto più è pesante il quark componente. La fig. 1 si riferisce al sistema della Ƴ costituito da una coppia bb̅ di quark-antiquark del sapore b (bottom o beauty). I mesoni Ƴ decadono per lo più secondo il diagramma di fig. 1 A che mostra l’annichilazione della coppia bb̅ che compone lo stato legato Ƴ in tre gluoni. I tre gluoni si manifestano sperimentalmente sotto forma di tre getti di adroni che si osservano come in fig. 1 B e C.

Tipi di adroni: adroni quasi stabili e risonanze adroniche

A parte il protone che è stabile, gli adroni si possono dividere in adroni quasi stabili e in risonanze adroniche a seconda che decadano per effetto delle interazioni elettromagnetiche o deboli oppure per effetto delle interazioni forti. Gli adroni quasi stabili [fra cui mesoni π^±, π⁰ (pioni), K^±, K⁰, K̅̅⁰ (kaoni), η ecc.; i barioni n (neutrone), Σ^±, Σ⁰, Λ, Ξ ⁰, Ω⁻ (iperoni)] sono quelli per i quali i decadimenti avvengono con violazione di isospin e/o di stranezza, charm ecc. Gli adroni quasi stabili e i protoni sono anche importanti perché è possibile in molti casi realizzare fasci di tali particelle da dirigere contro bersagli di materia e studiare i processi adronici risultanti.

Simmetria unitaria SU(3)

Si è già osservato che nel limite in cui si trascura la piccola differenza di massa tra i quark u e d lo spettro degli adroni si suddivide in multipletti di isospin degeneri (cioè formati da particelle di uguale massa). Analogamente, se con una approssimazione meno accurata si trascurano le differenze di massa tra i quark u, d, s si ottengono multipletti degeneri di adroni che comprendono al loro interno vari multipletti di isospin con differenti ipercariche. Tali multipletti si trasformano secondo rappresentazioni irriducibili del gruppo SU(3)_sapore delle matrici 3×3 unitarie a determinante uno (le matrici che ruotano tra loro i quark u, d, s). I quark formano un tripletto di SU(3): q=(u, d, s)=3̲, mentre gli antiquark formano un antitripletto: q̄=(ū, d̅, s̄)=3̲̅. I mesoni sono stati legati di una coppia di quark-antiquark. Quindi, per ogni configurazione spaziale e di spin, si avranno 9 stati, perché ogni quark può essere scelto in tre modi. Questi 9 stati si dividono in un multipletto di 8 stati (un ottetto) più un singoletto. Poiché i quark hanno spin 1/2, lo spin totale della coppia qq̄ può essere o zero o uno. Quindi i mesoni più leggeri formeranno un insieme di 9 stati di spin zero e 9 stati di spin uno. Altri mesoni più pesanti si otterranno come eccitazioni orbitali dei precedenti. In particolare, l’aggiunta di un’unità di momento angolare orbitale conduce a 4 nuovi insiemi di 9 mesoni con spin rispettivamente uguale a 2, 1, 1, 0. Tutti questi multipletti sono stati effettivamente osservati. I barioni sono stati legati di tre quark. Con tre quark di spin 1/2 si possono ottenere stati di spin totale uguale a 1/2 oppure 3/2. Inoltre in SU(3) vale la decomposizione generale: 3̲×3̲×3̲=10̲̲+8̲+8̲+1̲. I multipletti barionici più leggeri osservati sono infatti un ottetto di spin 1/2, comprendente il doppietto del nucleone e gli iperoni, e un decupletto di spin 3/2 comprendente le risonanze barioniche più leggere. Ogni multipletto osservato ha esattamente il contenuto previsto in isospin e ipercarica; nella fig. 2A è rappresentato il tripletto dei quark u, d e s; nella fig. 2B l’antitripletto dei corrispondenti antiquark; nella fig. 2C un ottetto mesonico, in particolare l’ottetto dei mesoni pseudoscalari, comprendente i pioni, i kaoni e l’eta; nella fig. 2D è rappresentato l’ottetto dei barioni più leggeri di spin 1/2 (il contenuto in ipercarica e isospin di questo ottetto è identico al precedente); nella fig. 2E il decupletto delle risonanze barioniche di spin 3/2 che comprende la Δ. La scoperta nel 1963 del barione Ω^– di stranezza −3 e isospin zero, composto da tre quark strani Ω^– ~ sss, necessario per completare il decupletto, ha rappresentato una tappa di grande importanza nello sviluppo del modello a quark.

Colore

Dalla sistematica degli adroni, interpretata nel modello a quark, si ottiene la prima evidenza dell’esistenza del colore. Consideriamo infatti la risonanza Δ⁺⁺ (1232), osservata nella diffusione pione-nucleone a energia nel centro di massa di circa 1230 MeV, con componente dello spin lungo una data direzione uguale a +3/2, cioè il valore massimo. Il contenuto in quark di questo stato è Δ⁺⁺ (1232) ~ u ↑ u ↑ u ↑, ove le frecce indicano schematicamente l’allineamento degli spin dei singoli quark. Tale stato è evidentemente simmetrico nei 3 quark che sono dello stesso sapore e si trovano nello stesso stato di spin, come pure è simmetrica la funzione d’onda parziale di tre quark con tutti i momenti angolari orbitali nulli. D’altra parte, dai principi fondamentali della meccanica quantistica segue che uno stato di più particelle identiche di spin semintero (fermioni) deve essere completamente antisimmetrico per scambio di una coppia qualsiasi di esse. La soluzione del problema sta appunto nell’esistenza del colore. I 3 quark in un barione sono di colore diverso, in una combinazione completamente antisimmetrica nel colore (cioè che cambia segno per scambio di due qualsiasi di essi) e in modo tale che il barione risulta complessivamente un singoletto sotto il gruppo di colore, ovvero è privo di cariche di colore. Più in generale, il colore spiega perché i barioni leggeri formano un ottetto di spin 1/2 e un decupletto di spin 3/2, in quanto queste sono le uniche configurazioni compatibili con l’antisimmetria e la neutralità nel colore e il fatto che i quark sono fermioni. In assenza del colore i barioni leggeri formerebbero un ottetto di spin 1/2 e un singoletto di spin 3/2.

Cromodinamica quantistica (QCD)

La scoperta dei quark colorati come costituenti degli adroni ha permesso di costruire una teoria di campo delle interazioni f. che la complessità apparente degli adroni aveva in precedenza reso impossibile. Il gruppo di simmetria di colore, SU(3)_colore è il gruppo delle matrici che agiscono sui tre stati di quark di colore diverso. Non bisogna confondere questo gruppo con SU(3)_sapore, già menzionato, che agisce sui quark di sapore u, d, s ed è utile per la classificazione dei multipletti adronici. La struttura matematica è la stessa, ma il significato fisico è diverso. Il primo è un gruppo di simmetria approssimata, valida se si trascurano le differenze di massa tra i quark leggeri u, d e s, mentre il secondo è una simmetria esatta, almeno per quanto è dato di conoscere al momento. In analogia con l’elettrodinamica quantistica (➔ elettrodinamica), si assume che la simmetria di colore sia valida per trasformazioni indipendenti in ogni punto dello spazio-tempo, ovvero che si tratti di una simmetria locale o, come anche si dice, di gauge. A differenza dell’elettrodinamica, in cui è presente una sola carica conservata (la carica elettrica), in QCD si hanno 8 cariche conservate che soddisfano relazioni algebriche (commutatori) non banali. Una teoria di gauge è completamente specificata una volta dato il gruppo di simmetria e i campi materiali (i quark, in questo caso). In particolare esistono tanti bosoni di gauge di spin 1 e massa nulla che mediano le interazioni tra i campi materiali quante sono le cariche conservate. Quindi in QCD ci sono 8 gluoni colorati che interagiscono non solo con i quark ma anche tra loro, mentre in elettrodinamica c’è un solo fotone, elettricamente neutro. La QCD è dunque una teoria delle interazioni tra quark e gluoni. Ma i quark e i gluoni non si osservano direttamente, in quanto sono confinati, come descritto in precedenza. Pertanto non è facile verificare sperimentalmente la QCD. Una proprietà importante da questo punto di vista è la libertà asintotica, già ricordata, che consiste nel fatto che l’interazione diminuisce a piccole distanze. Questo comportamento delle interazioni a corte distanze si può osservare in esperienze ad alta energia e grandi momenti trasferiti, i cosiddetti processi altamente anelastici. In queste condizioni è possibile ottenere delle predizioni quantitative esplicite facendo uso della teoria delle perturbazioni. I processi più importanti per una verifica quantitativa della teoria sono l’annichilazione elettrone-positrone e la diffusione profondamente inelastica leptone-nucleone, ottenuta mediante fasci di elettroni, muoni, neutrini o antineutrini contro bersagli materiali. La libertà asintotica porta a prevedere che in tali processi, ad alte energie e momenti trasferiti, si debba osservare una semplificazione della dinamica che tende a evidenziare le proprietà dei cosiddetti partoni, cioè dei campi fondamentali, i quark e i gluoni. La sezione d’urto totale adronica di annichilazione e⁺−e^– divisa per la sezione d’urto e⁺−e^–→μ⁺+μ^– ad alte energie tende alla somma delle cariche quadrate dei quark prodotti, con correzioni calcolabili che sono piccole come conseguenza della libertà asintotica. Lo stato finale è costituito per lo più da due getti di adroni molto collimati ed emessi in direzioni opposte nel centro di massa della reazione. Ogni getto è dovuto a un quark o antiquark, come è dimostrato, per es., dal fatto che la distribuzione angolare dei getti è identica a quella prevista per una coppia di particelle puntiformi di spin 1/2. I getti si originano in quanto i quark sono confinati. Infatti, quando il quark e l’antiquark prodotti nell’interazione primaria si allontanano dal punto di interazione, è necessario che la carica di colore sia neutralizzata per emissione di tutta una serie di coppie quark-antiquark che si materializzano in adroni. Il colore viene scambiato tra i due getti per il tramite di un gran numero di adroni lenti, che sono in un certo senso in comune tra i due getti. Con minore frequenza, nell’annichilazione e⁺−e^– si presentano eventi con tre getti ben distinti. In questo caso, oltre alla coppia quark-antiquark si è anche prodotto un gluone di alta energia, irradiato da uno dei quark primari. Gli eventi a tre getti costituiscono una delle prove sperimentali più dirette dell’esistenza dei gluoni. Dovrebbero anche esistere degli adroni composti unicamente da gluoni (gluonio o glue-ball) ma la loro rivelazione è molto difficile e non esistono prove sicure che alcuni candidati che sono stati proposti siano effettivamente stati legati senza colore di gluoni. Nella diffusione profondamente inelastica di leptoni su materia si esplora il contenuto in partoni del nucleone a piccole distanze e le distribuzioni delle frazioni di impulso trasportate da ciascun componente. Le variazioni con il momento trasferito di tali distribuzioni (violazioni dell’invarianza di scala o scaling) sono calcolabili con precisione e costituiscono una base sperimentale molto articolata e quantitativa per la teoria. Le esperienze con fasci incrociati protone-antiprotone al CERN di Ginevra hanno aggiunto nuove spettacolari conferme della cromodinamica quantistica. Dal punto di vista teorico riveste una notevole importanza lo studio degli aspetti non perturbativi della QCD, rilevanti per il confinamento e le proprietà statiche e dinamiche degli adroni (modello a stringa, modello a bag o sacca) come pure degli effetti topologici (monopoli, cariche topologiche, soluzioni classiche con carica topologica non nulla). Un metodo di approssimazione molto potente consiste nel sostituire allo spazio-tempo continuo della teoria dei campi ordinaria uno spazio-tempo discretizzato, simile a un reticolo cristallino, e di effettuare complesse simulazioni al computer nella approssimazione discretizzata della teoria (QCD su reticolo), per poi estrapolare i risultati al caso continuo.