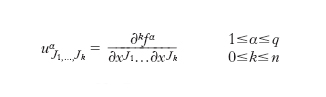getto

Botanica

Sinonimo di germoglio o di pollone (➔ pollone).

Matematica

Spazio dei getti (ingl. jet space)

Quello spazio le cui coordinate rappresentano variabili indipendenti, dipendenti e derivate delle variabili dipendenti. Lo studio di equazioni e sistemi differenziali a derivate parziali, e in particolare ordinarie, si semplifica spesso notevolmente per la eventuale esistenza di gruppi di simmetrie. La ricerca di questi ultimi talora viene fatta sostituendo la ordinaria nozione di sistema differenziale con un oggetto geometrico di più facile intuizione. Lo spazio dei g. nasce dall’esigenza di definire uno spazio i cui elementi rappresentino opportunamente un sistema differenziale. Sia f: X→U, X⊆R^p, U⊆R^q una funzione, di opportuna classe di differenziabilità tale che u=f(x)=(f¹(x), ..., f^q(x)), x=(x¹, ..., x^p) e per la quale esistono q∙p_k derivate parziali di ordine k, con p_k=(^p+k−1_k ); lo spazio U_k=R^q∙p_k rappresenta con le sue coordinate tutte le derivate di ordine k, mentre lo spazio prodotto cartesiano U⁽ⁿ⁾=U×U₁× ... ×U_n rappresenta con le sue coordinate la funzione e tutte le sue derivate fino all’ordine n. Si definisce g. n-esimo, o di ordine n, di f la funzione u⁽ⁿ⁾ definita dalla relazione

Poiché u⁽ⁿ⁾: X→U⁽ⁿ⁾ è un vettore le cui componenti rappresentano i valori di f e di tutte le sue derivate calcolate nel punto x ∈ X fino all’ordine n, lo spazio dei g. X×U⁽ⁿ⁾ dello spazio X×U rappresenta, con le sue coordinate, le variabili indipendenti, le variabili dipendenti e le derivate delle variabili dipendenti, fino all’ordine n.