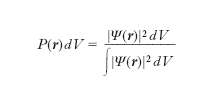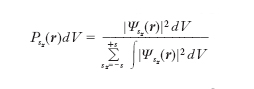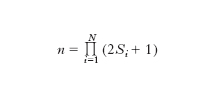funzione

Biologia

L’attività propria di una cellula, o di una sua parte, o di un organo, o di un sistema organico. Oggetto di studio della fisiologia, è intimamente legata alla forma o struttura, oggetto di studio della morfologia. Forma e f. sono due aspetti sotto cui ci si presenta il fenomeno della vita. Non ha senso domandarsi quale delle due preesista e determini l’altra, perché non esiste l’una senza l’altra; è quindi priva di fondamento la frase «la f. crea l’organo», che è divenuta un luogo comune della volgarizzazione delle teorie evoluzionistiche lamarckiane. La formulazione corretta è «la f. sviluppa l’organo».

Diritto

Funzione amministrativa

Con riferimento alla classica tripartizione dei poteri in legislativo, giurisdizionale ed esecutivo, affidati rispettivamente al parlamento, alla magistratura e al governo, locuzione utilizzata per indicare l’insieme dei compiti attribuiti all’amministrazione, ma di fatto priva di valore giuridico. Infatti, la separazione dei poteri e delle f. non corrisponde né all’ordinamento comunitario, che manca di questa netta distinzione – la Commissione europea, per es., ha compiti sia di iniziativa legislativa sia di natura contenziosa – né all’ordinamento nazionale, che conosce diversi ibridi, quali le autorità indipendenti, aventi compiti riconducibili a più di un potere, le f. amministrative affidate ai giudici (come l’attività di volontaria giurisdizione), le f. normative svolte dall’apparato esecutivo (come il potere regolamentare), le f. di risoluzione dei conflitti svolte dall’amministrazione (attività amministrativa contenziosa).

In un’altra accezione, il termine f. si utilizza, in contrapposizione a quello di servizio, per indicare l’attività di tipo autoritativo che contraddistingue la pubblica amministrazione. Tale distinzione, propria dello Stato liberale, può considerarsi superata in termini generali, mentre si riscontra in alcune disposizioni normative particolari sia dell’ordinamento nazionale, sia di quello comunitario. Nell’ordinamento italiano, l’art. 357 c.p. definisce, ai soli fini dell’applicazione della legge penale, la f. amministrativa quale attività disciplinata da norme di diritto pubblico e da atti autoritativi, e caratterizzata dalla formazione e dalla manifestazione della volontà della pubblica amministrazione o dal suo svolgersi per mezzo di poteri autoritativi o certificativi; e l’art. 358 c.p. qualifica il servizio come un’attività disciplinata nelle stesse forme della pubblica f., ma caratterizzata dalla mancanza dei poteri tipici di quest’ultima. Nell’ordinamento comunitario, invece, la nozione è stata utilizzata come criterio per limitare la deroga alla libera circolazione dei lavoratori all’interno della Comunità che, ai sensi dell’art. 39, par. 4, TCE, si applica agli impieghi nella pubblica amministrazione. In attuazione di tale norma, l’art. 8 reg. CEE 1612/68 ha specificato che il lavoratore cittadino di uno Stato membro può essere escluso, sul territorio di un altro Stato membro, dall’esercizio di una f. di diritto pubblico e la Corte di Giustizia ha chiarito che la disposizione trova applicazione solamente per quegli impieghi che implicano una partecipazione, diretta o indiretta, all’esercizio del pubblico potere e alle f. che hanno per oggetto la salvaguardia degli interessi generali dello Stato o delle altre comunità pubbliche e non anche per i servizi, quali, per es., istruzione, sanità, trasporti, poste e telecomunicazioni, energia, ricerca.

Con altro significato, più rilevante per il diritto amministrativo, il termine è utilizzato per indicare che l’attività amministrativa è f., nel senso che l’amministrazione, in tutti i suoi elementi (organizzazione, personale, finanza, attività), deve essere in rapporto con i fini pubblici. Tale correlazione è sempre presente, anche quando, nel caso del ricorso delle amministrazioni a istituti propri del diritto privato (contratti, costituzione di società per azioni, gestione di beni pubblici ecc.), risulta meno evidente e assume forme giuridiche diverse.

Più diffusamente, si parla, al plurale, di funzioni pubbliche con riferimento all’insieme delle attività svolte dagli apparati amministrativi dello Stato e degli altri enti o figure del settore pubblico. In questo senso, la f. si compone in realtà di un insieme di f., le quali sono state oggetto di studio delle scienze politiche e di una parte della dottrina giuridica. Sotto il primo profilo, il tema della progressiva espansione delle f. pubbliche – dai campi d’azione tradizionali (difesa, affari interni ed esteri) a quelli legati allo stato sociale (sanità, istruzione, protezione sociale) o volti all’intervento nell’economia (finanza, assicurazioni, credito, fonti di energia, comunicazioni) o alla tutela di particolari settori (ambiente) – si connette alla problematica relativa all’evoluzione storica dello Stato liberale, volta a garantire l’eguaglianza dei cittadini in senso non soltanto formale, ma anche sostanziale. Una parte della scienza giuridica ha mostrato un certo disinteresse per questa parte del diritto amministrativo mentre un’altra, di fronte al moltiplicarsi delle f. pubbliche, si è occupata sia di individuarne caratteri ed elementi, sia di analizzare la loro ripartizione fra i vari apparati amministrativi.

Quanto ai caratteri, la f. amministrativa non è libera ma soggetta a procedimenti e controlli (se volta all’emanazione di atti giuridici), ha natura permanente, nel senso che non è circoscritta al raggiungimento di uno scopo concreto o all’adozione di un singolo atto, e trova sempre il suo fondamento in una norma. Più in particolare, dall’analisi delle norme che le disciplinano, emergono quattro elementi fondamentali delle f. amministrative: a) la materia individua il campo d’intervento; b) le attribuzioni definiscono i compiti assegnati dalla legge all’amministrazione nell’ambito di una data materia; c) il fine indica lo scopo generale dell’azione amministrativa, non legato a un singolo atto; d) i destinatari sono i soggetti ai quali la f. è rivolta (la generalità dei cittadini, o gruppi o singoli, definiti dalle norme).

In base all’ordinamento comunitario, i rapporti fra Comunità e Stati sono regolati dai principi di sussidiarietà (TCE, art. 5) e leale cooperazione (TCE, art. 10), per effetto dei quali le f. amministrative possono essere ripartite tra i due livelli, o svolgersi in modo concorrente, attraverso procedimenti composti. In questo secondo caso, sono responsabili delle singole fasi ora l’amministrazione comunitaria, ora quella nazionale, ora persino quella di altri Stati membri. Nell’ordinamento nazionale, a seguito della riforma del titolo V della seconda parte della Costituzione, le f. amministrative non sono più distribuite in base al criterio della materia, in correlazione con la potestà legislativa, ma sono attribuite ai comuni, «salvo che, per assicurarne l’esercizio unitario, siano conferite a Province, Città metropolitane, Regioni e Stato, sulla base dei principi di sussidiarietà, differenziazione ed adeguatezza» (art. 118).

Economia

Funzione della produzione

La relazione che intercorre tra la quantità di uno o più beni o servizi che si vuol produrre o si è prodotta e la quantità dei vari fattori di produzione che è necessario impiegare o che si è impiegata; la f. (quella più in uso prende il nome degli economisti C.W. Cobb e P.H. Douglas che furono i primi a utilizzarla) è riferita sia alle singole imprese, sia all’economia nel suo complesso (f. aggregata delle produzioni) e, partendo dall’assunto che i fattori produttivi, in particolare capitale e lavoro, siano sempre sostituibili tra loro, dice che per ciascun livello di produzione la sostituzione avviene quando mutano i prezzi relativi dei fattori stessi.

Fisica

In elettronica, il termine è talora usato come sinonimo di ‘segnale’.

Generatore di funzione

Generatore di segnali capace di fornire tensioni periodiche di varia forma (sinusoidali, quadrate, triangolari, impulsive ecc.) e di frequenza variabile entro un ampio campo, costituito sostanzialmente da un oscillatore a rilassamento seguito da circuiti differenziatori e integratori; apparecchi del genere, inizialmente realizzati per le calcolatrici analogiche, trovano attualmente impiego generale in elettronica (analisi dei circuiti, servomeccanismi ecc.).

Funzione d’onda

In meccanica quantistica (➔ meccanica) a ogni stato di un sistema si può associare una f. d’onda che lo determina completamente. Per una particella senza spin la f. d’onda Ψ(r) è l’ampiezza di probabilità che in una misura di posizione si trovi la particella nel volume infinitesimo dV intorno al punto r≡(x, y, z). Ovvero la corrispondente probabilità è data da

La f. d’onda è determinata a meno di un fattore di normalizzazione e di una fase. Per una particella con spin sħ, ove s è intero o semintero, la f. d’onda ha 2s+1 componenti. Il modulo quadro di ciascuna componente determina la probabilità P_sz (r) dV di trovare particelle in dV con componente s_z dello spin lungo la direzione dell’asse z:

Per un sistema a N particelle di spin s_iħ (i=1, 2, ..., N) la f. d’onda ha n componenti,

e dipende dagli N vettori coordinati r_i. Invece che con la f. d’onda nello spazio delle configurazioni ora descritta, si può equivalentemente rappresentare lo stato del sistema mediante la f. d’onda nello spazio degli impulsi (o quantità di moto), definita in modo del tutto analogo.

Funzione di struttura

In fisica delle particelle elementari, le f. di struttura di un sistema non puntiforme (un adrone, un nucleo, un atomo ecc.) sono quelle f. delle variabili cinematiche che caratterizzano l’accoppiamento del sistema a una o più correnti. Nel caso di una singola corrente si parla di fattore di forma.

Istruzione

Funzione docente

Insieme delle attività volte ad attuare il processo didattico-apprenditivo nel senso della promozione dello sviluppo umano, culturale, civile e professionale degli alunni, sulla base delle finalità e degli obiettivi previsti dagli ordinamenti scolastici. La f. si fonda sull’autonomia culturale e professionale dei docenti e si esplica nelle attività individuali e collegiali e nella partecipazione alle attività di aggiornamento e formazione in servizio. In attuazione dell’autonomia scolastica i docenti, collegialmente, elaborano, attuano e verificano, il Piano dell’offerta formativa (POF). Per agevolare la realizzazione del POF il collegio dei docenti individua alcuni docenti ai quali affidare specifici compiti. Le relative f. vengono dette f. strumentali al piano dell’offerta formativa.

Linguistica

Il ruolo che un’unità qualsiasi della frase (fonema, morfema, unità lessicale, sintagma) svolge nella struttura grammaticale della frase stessa, cioè dell’intero enunciato. Si distingue talora tra funzione significativa, quella che svolge l’elemento significante della parola in seno alla frase, e funzione distintiva, quella svolta dal fonema o da altro elemento fonico in seno alla parola (per es., è distintiva la funzione dell’accento in pero e però).

Con significato diverso, affine a quello della matematica, è detta f., in glossematica, ogni relazione tra due termini, che possono essere entrambi costanti o entrambi variabili o uno costante e l’altro variabile (➔ funzionalismo).

Matematica

Definizione di funzione

Una quantità y si dice f. di una quantità x o di più quantità x₁, x₂, ..., variabili in un certo insieme C, se esiste una determinata legge che a ogni valore o sistema di valori di C assegnati alla variabile x ovvero alle variabili x₁, x₂, ..., associa un unico valore della variabile y; questa dipendenza si indica con y=f(x) o con y=f(x₁, x₂, ...) o con simboli analoghi. Le variabili x o x₁, x₂, ..., si dicono variabili indipendenti; la y è la f. o variabile dipendente. Una f. si dice reale o complessa a seconda che tali siano i suoi valori; si dice f. di variabile reale o di variabile complessa a seconda che la sua variabile indipendente sia suscettibile di assumere soltanto valori reali o anche valori complessi. Esistono svariati tipi di f., ciascuno dei quali è denotato con un termine o un simbolo proprio (per es., funzione continua, funzione derivabile, funzione di Bessel ecc.).

Funzione di punto, funzione di insieme, funzionale

Per esprimere il fatto che la f. y=f(x₁, x₂, ..., x_n) dipende dalle n variabili indipendenti x₁,x₂, ..., x_n, si dice che è f. del punto P avente per coordinate, in uno spazio a n dimensioni, i valori delle variabili indipendenti, e si scrive y=f(P). L’insieme di definizione della f. diviene quindi un insieme nello spazio suddetto. Una f. però, nell’accezione più generale del termine, non è necessariamente una f. di punto. Per es., l’area A racchiusa da una curva piana, chiusa, regolare, non intrecciata, di data lunghezza C dipende dalla intera curva C: A=f(C), essendo C variabile in una ‘famiglia di curve’. Una f. di linea è un particolare esempio di f. di insieme (➔ anche funzionale). Allo stato attuale della matematica, il concetto più generale di f. coincide con quello di applicazione (o più in generale di corrispondenza) di un insieme in un altro; precisamente, dati due qualsiasi insiemi X, Y, si dice f. una legge che a ogni elemento x di X associa un elemento y di Y (detto immagine di x); si scrive f:X→Y; X è l’insieme di definizione, o dominio, della f.; l’insieme Y*⊆Y, descritto da y al variare di x in X si dice insieme di variabilità o codominio. Una f. è detta poi suriettiva se Y*=Y, iniettiva se nessun elemento di Y è immagine di più di un elemento di X; si dice biiettiva una f. suriettiva e iniettiva.

Funzione a un valore, a più valori, a infiniti valori

Si chiama funzione a un valore (o monodroma o univoca o uniforme), una f. tale che, per ogni scelta della o delle variabili indipendenti nel campo di definizione, dia un solo valore per la variabile dipendente; per es., y=x²+5x+2.

Si chiama funzione a più valori (o polidroma o plurivoca o pluriforme) una f. tale che, per ogni scelta della o delle variabili indipendenti nel campo di definizione, dia due o più valori (in numero però finito) per la variabile dipendente; per es., y=+√‾‾x.

Si chiama funzione a infiniti valori (o infinitivoca o infinitiforme) una f. che, per ogni scelta della o delle variabili indipendenti nel campo di definizione, dia luogo a infiniti valori della variabile dipendente; per es. y=arcsenx (quando non si pongano limitazioni per il valore di y).

Funzione inversa

Data una f. univoca biiettiva y=f(x), accade che ciascuno dei valori di y proviene da un unico valore di x; questa legge, che a ogni y associa in questo modo un x, è perciò una funzione x=ϕ(y), si dice f. inversa della funzione data, e si indica usualmente con x=f^–1(y) (da non confondersi con la f. reciproca 1/f(x)=[f(x)]^–1). Una f. ammette la f. inversa in un intervallo in cui sia sempre crescente (➔ monotono) o sempre decrescente: l’inversa di y=x² è x=+√‾‾y (per x≥0, y≥0), l’inversa di y=e^x è x=ln y (per y>0) ecc.

Funzione composta (o funzione di funzione)

Se y=f(u) e u=ϕ(x) sono due funzioni date, allora si ha che y è funzione di x:y=f [ϕ (x)]=F (x), e tale f. si dice composta mediante le due f. date; si dice anche che y è f. di una f. di x (non si confonda tale concetto con quello di funzionale, sostanzialmente diverso). Per poter parlare della f. composta y=F(x) bisogna, naturalmente, supporre che l’insieme di variabilità di ϕ sia contenuto (anche soltanto in modo parziale) nell’insieme di definizione della funzione. Più in generale, se u_i=ϕ_i(x₁, x₂, ..., x_n) (i=1, 2, ..., m), e y=f (u₁, u₂, ..., u_m) sono f. date, si dice che y è f. delle x_1, x₂, ..., x_m, composta mediante le u₁, u₂, ..., u_m.

Le funzioni nell’analisi matematica

Le f. più usate nell’analisi matematica e nelle sue applicazioni sono le funzioni numeriche di variabili numeriche, cioè le f. y=f(x) nelle quali i valori assunti tanto dalla variabile indipendente x quanto dalla variabile dipendente y sono numeri, reali o complessi. Si hanno così le seguenti possibilità: funzione reale di variabile reale (per es., y=senx, per x reale), funzione reale di variabile complessa (per es., y=|x|, per x complesso), funzione complessa di variabile reale (per es. y=√‾‾x, per x reale qualsiasi), funzione complessa di variabile complessa (per es., y=x²+1, per x complesso). Una funzione numerica di variabile reale può essere rappresentata su un piano cartesiano. L’insieme di punti del piano cartesiano le cui coppie coordinate sono date dai valori x_i e y_i=f(x_i) costituisce il grafico, o diagramma, della funzione. Una f. (numerica di variabile reale o complessa) può essere data esplicitamente mediante una espressione analitica, vale a dire come il risultato di un insieme di operazioni da eseguire su numeri (costanti) e sulle variabili indipendenti; può invece essere data implicitamente da una relazione analitica tra la y e le variabili indipendenti, nel qual caso si parla di funzione implicita: il passaggio a forme esplicite è oggetto di un teorema di U. Dini. Il caso più semplice di dipendenza esplicita è quello delle funzioni razionali, intere e fratte, nelle quali la y è data come un polinomio o rispettivamente come un quoziente di polinomi nelle variabili indipendenti. Il caso più semplice di dipendenza implicita è quello delle funzioni algebriche, che sono le f. definite implicitamente da relazioni del tipo f(x,y)=0 nelle quali f(x,y) è un polinomio nelle due variabili x, y (per es., y²−x=0). Quando una f. non è né razionale né algebrica, si chiama trascendente. Si chiamano poi trascendenti elementari le potenze di x con esponente irrazionale, le f. circolari e iperboliche e le loro inverse, la f. esponenziale e la f. logaritmica. Si chiamano f. rappresentabili analiticamente quelle che si possono rappresentare mediante algoritmi infiniti (serie, prodotti infiniti, ecc.) a partire dalle f. razionali intere. In quest’ordine d’idee si introduce, per le f. rappresentabili analiticamente, la classificazione di R. L. Baire: le f. continue si diranno appartenere alla classe 0 di Baire, in quanto, come si dimostra, ogni f. continua in un intervallo finito si può esprimere come somma di una serie uniformemente convergente di f. razionali intere; si diranno appartenere alla classe 1 di Baire le f. ottenute come somma di una serie di funzioni di classe 0, e che non siano esse stesse di classe 0; e così via, per induzione (transfinita) rispetto al numero n, si dice che appartengono alla classe n di Baire quelle f. che si possono esprimere come somme di serie di funzioni di classe < n, non essendo esse stesse di classe <n.

Il ramo più sviluppato della teoria delle f. di variabile reale è quello delle f. reali a un valore di una (o più) variabili reali.

Funzioni di verità

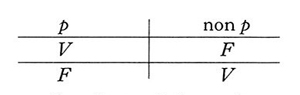
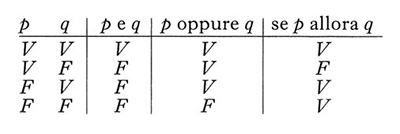
In logica matematica, particolare tipo di f. che ha sia come argomenti sia come valore i valori di verità Vero (V) e Falso (F). F. di verità di particolare importanza sono i connettivi (negazione, congiunzione, disgiunzione, implicazione ecc.), i quali non sono quindi in sé veri o falsi, ma corrispondono a operazioni che alla verità o falsità di certe proposizioni associano la verità o falsità di un’altra proposizione, costruita a partire dalle precedenti tramite i connettivi in questione. Per es., la negazione viene interpretata come quella f. a un argomento che assume valore V se la proposizione a cui si applica la negazione è falsa, e viceversa; si può rappresentare tale f. con il seguente schema (o tavola di verità):

dove, nella colonna di destra, è segnato il valore che la f. (e quindi la proposizione ‘non p’) assume di volta in volta. La congiunzione viene interpretata come quella f. di verità binaria che ha valore V solo se il valore di verità delle due proposizioni a cui la congiunzione si applica è sempre V. La disgiunzione viene in genere intesa come quella f. binaria la quale ha valore F solo se applicata a proposizioni che sono entrambe false; corrisponde quindi alla disgiunzione debole o alternativa, che è vera purché almeno una delle due proposizioni lo sia. Ancor più particolare è il caso dell’implicazione; essa è vera non solo quando antecedente e conseguente sono entrambi veri, ma anche nel caso in cui l’antecedente è falso e il conseguente vero, e in quello in cui antecedente e conseguente sono entrambi falsi. Lo schema che segue riassume le tavole di verità che rappresentano i connettivi appena descritti.

Un teorema logico, detto di completezza funzionale, afferma che, data una qualunque f. di verità f a n argomenti, per ogni n esiste uno schema di enunciato costruito nel linguaggio simbolico usando solo, quali connettivi, la negazione e la congiunzione, o la negazione e la disgiunzione, o la negazione e l’implicazione, tale che a esso corrisponda una f. di verità coincidente con f (nel senso che per gli stessi argomenti assume gli stessi valori di f). Oltre a quelli qui indicati, vi sono poi altri connettivi che possono sostituirsi ai precedenti e che corrispondono ad altre f. di verità.