intorno

Enciclopedia on line

fig. A

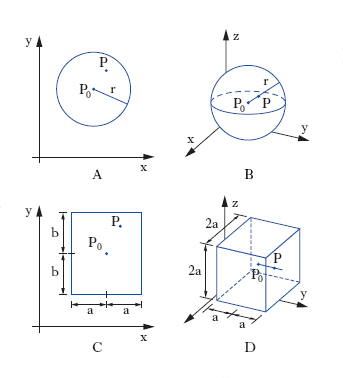
In topologia, sottoinsieme associato a un punto dello spazio, che gode di certe proprietà, le quali corrispondono all’idea intuitiva di ‘vicinanza’. A seconda che queste proprietà siano più o meno restrittive, lo spazio stesso viene a coincidere con l’uno o l’altro tipo di spazio topologico. Se, quando ci si riferisce allo spazio numerico, come i. di P si prende l’insieme dei punti interni a una sfera di centro P, si ha lo spazio euclideo. Intorno circolare (fig. A) di un punto P0 del piano è l’insieme dei punti P tali che PP0<r, con r positivo prefissato; il numero r prende anche il nome di raggio dell’i. circolare.

Intorno sferico (fig. B) di un punto P0 nello spazio (o in un iperspazio) è l’insieme di punti P tali che PP0<r, con r positivo prefissato, detto raggio dell’i. sferico. Intorno rettangolare (fig. C) di un punto P0(x0, y0) nel piano è l’insieme dei punti P(x, y) tali che |x−x0|<a, |y−y0|<b con a b positivi fissati; se a=b si ha l’intorno quadrato. Nello spazio è l’insieme dei punti per cui

|x−x0|<a, |y−y0|<b, |z−z0| < c

e analogamente negli iperspazi; se a=b=c si parla di i. cubico (fig. D) ecc. I. del punto all’infinito nel piano della variabile complessa è l’insieme dei punti esterni a una circonferenza o a un rettangolo.

Per le relazioni tra il concetto di i. e quello di insieme aperto ➔ topologia.

Vedi anche
omeomorfismo In matematica, corrispondenza biunivoca e bicontinua tra due spazi topologici S e S′, tale cioè che: a) a ogni punto P di S associ uno e un sol punto P′ di S′ e viceversa (corrispondenza biunivoca); b) fissato a piacere un intorno I′ di un qualunque punto P′ di S′, esista un intorno I del punto P corrispondente ... singolarità fisica In fluidodinamica, qualsiasi punto del campo di moto di un fluido irrotazionale, non viscoso e a densità costante in cui la funzione potenziale di velocità Φ assuma valore infinito o non sia monovalore (detto più propriamente punto singolare). Le s. possono essere puntiformi (sorgenti e pozzi), ... frontiera Linea di confine (o anche, spesso, zona di confine, concepita come una stretta striscia di territorio che sta a ridosso del confine), soprattutto in quanto ufficialmente delimitata e riconosciuta, e dotata, in più casi, di opportuni sistemi difensivi. In senso figurato, linea che separa nettamente ambienti ... rivestimento Il materiale con cui si è ricoperta una superficie, a scopo protettivo o decorativo. Biologia Epiteli di r. Epiteli che tappezzano la superficie esterna del corpo e le pareti di cavità interne, comunicanti o meno con l’esterno. Botanica R. (o indumento) ceroso è il complesso delle sostanze cerose che ...
Tag
Altri risultati per intorno
  • intorno
    Enciclopedia della Matematica (2013)
    intorno in analisi, concetto che allude alla totalità di elementi “vicini” a un elemento dato. Poiché nella retta reale è definita la distanza tra due punti P1 e P2 come la lunghezza (senza segno) del segmento P1P2, si definisce intorno (simmetrico) di un qualsiasi punto P0 (al finito) dell’asse x l’insieme ...
  • intorno
    Dizionario delle Scienze Fisiche (1996)
    intórno [Uso sostantivato dell'avv., comp. di in- e torno "in giro"] [ALG] Sulla retta numerica R, i. di un punto P è ogni intervallo aperto che lo contiene. Più in generale, i. è un sottoinsieme I di uno spazio associato a un punto P di questo, che gode di certe proprietà, le quali corrispondono alle ...
Vocabolario
intórno¹
intorno1 intórno1 avv. [comp. di in-1 e torno1]. – 1. In giro, in posizione o con movimento pressappoco circolare: c’era gran folla i.; aveva molta gente i.; volgere lo sguardo, muovere gli occhi i.; con valore aggettivale: i luoghi intorno,...
intórno²
intorno2 intórno2 s. m. [uso sostantivato dell’avv.]. – 1. ant. Dintorno, luogo circostante: scorrendo e predando sempre e da ogni banda tutti gli intorni de’ loro vicini (P. F. Giambullari). 2. In matematica, in partic. in topologia, è...