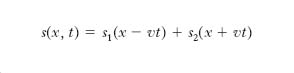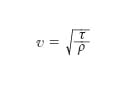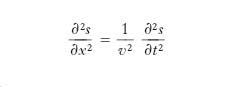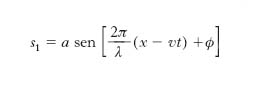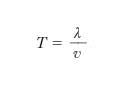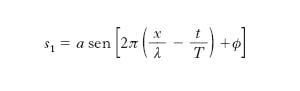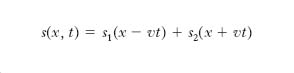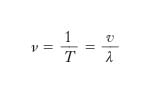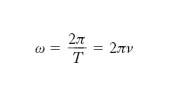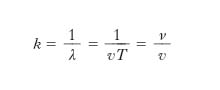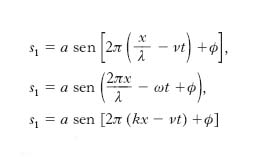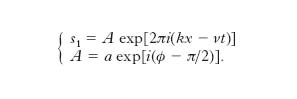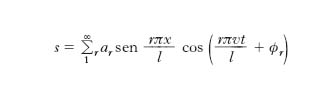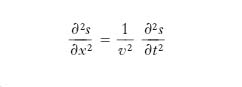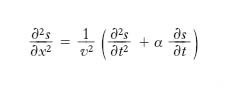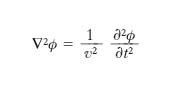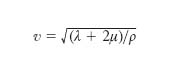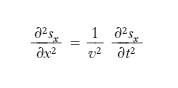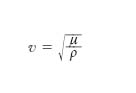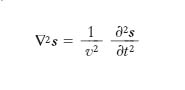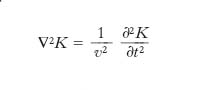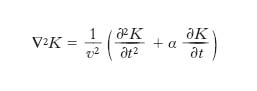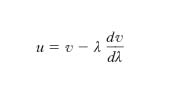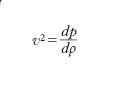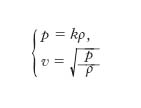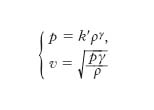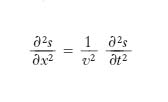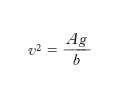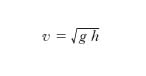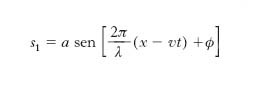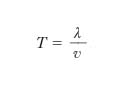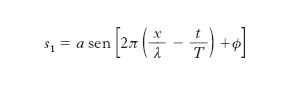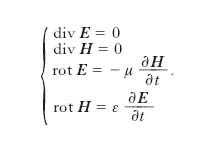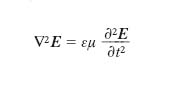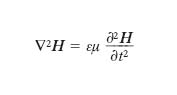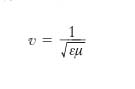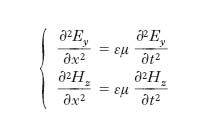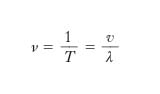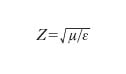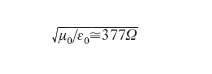onda

Con riferimento a un dato mezzo fisico (acqua, aria ecc.), perturbazione determinatasi in un punto del mezzo che si propaga nello spazio trasportando energia ma non materia.

Fisica

Propagazione per onde

Si parla di propagazione per o. di una perturbazione tutte le volte che in uno o più punti di un corpo, o più genericamente di un mezzo o di un ente fisico, si determina una perturbazione di qualche caratteristica (per es., in un corpo elastico uno spostamento di suoi punti dalle loro posizioni di riposo) e questa perturbazione si trasmette dai punti dove si è generata a zone a essi circostanti, trasportando energia ma non materia. La sorgente da cui nasce la perturbazione può essere estesa o (approssimativamente) puntiforme. I punti raggiunti dalla perturbazione a un dato istante costituiscono generalmente una superficie che prende il nome di superficie d’o., o fronte d’o., all’istante considerato. La direzione di propagazione in un dato punto P di un fronte d’o. è la direzione in cui si propaga una porzione infinitesima intorno a P del fronte stesso.

Il raggio di propagazione dell’o. (o più semplicemente il raggio) è la linea che in ogni punto è tangente alla direzione di propagazione di una data porzione infinitesima del fronte d’onda. Non è detto che i raggi siano rettilinei: lo sono nel caso in cui le superfici d’o. siano costituite da sfere concentriche (o. sferiche) e quindi i raggi di propagazione siano i raggi stessi di queste sfere; come anche in quello in cui le superfici siano piani paralleli (o. piane) e i raggi quindi siano le rette, parallele, normali a tali piani. Se la perturbazione associata all’o. può essere individuata da un vettore, l’orientamento di questo rispetto al raggio può essere a priori qualsiasi: particolare importanza ha il caso che il vettore della perturbazione abbia direzione coincidente con la direzione di propagazione (o. longitudinali) e quello che esso risulti normale alla direzione di propagazione (o. trasversali): per es., il suono si propaga negli aeriformi per o. longitudinali, la luce per o. trasversali.

Lungo ogni direzione la propagazione può, a priori, avvenire in un verso o nel verso opposto: così l’o. si dice progressiva o retrograda a seconda che la propagazione avvenga nel verso fissato come positivo sulla direzione considerata o nel verso opposto, come verso positivo assumendosi di solito quello di allontanamento dalla sorgente. Un’o. si dice poi permanente se le sue caratteristiche rimangono inalterate, indefinitamente, lungo ogni raggio. Un’o. permanente è peraltro una pura astrazione poiché in pratica l’o. è sempre smorzata in conseguenza della distribuzione su fronti d’o. sempre più ampi e dell’eventuale dissipazione di una parte dell’energia che essa convoglia. Dalla sovrapposizione di o. che si propaghino lungo una stessa direzione può non risultare una propagazione ondosa: è il caso, per es., delle cosiddette o. stazionarie.

Numerosi sono i fenomeni fisici con carattere ondoso, e dalla natura di ciascuno di essi si denominano le onde. Una prima grande ripartizione può farsi tra o. elastiche e o. elettromagnetiche: costituite, le prime, da una perturbazione oscillatoria delle particelle materiali di un mezzo elastico, e le seconde dalla propagazione, in un mezzo qualunque o nel vuoto, di un campo elettrico e di un campo magnetico, entrambi variabili. In seno poi a queste due principali categorie ulteriori distinzioni possono farsi in relazione a caratteristiche intrinseche dell’o., per es., in base al carattere longitudinale o trasversale, progressivo o stazionario, in base alla forma dei fronti d’o., alla frequenza ecc., ovvero in base alle caratteristiche del mezzo.

O. nelle corde elastiche vibranti

fig. 1

Si consideri un filo elastico (corda elastica) omogeneo, preliminarmente disposto secondo la retta x, soggetto a una tensione costante, che a un certo istante prenda a vibrare, per l’intervento di opportune sollecitazioni, in modo che i suoi elementi compiano piccole oscillazioni in un determinato piano α (fig. 1) individuato dalla retta x (che si assume come asse delle ascisse, fissando su essa un’origine e un verso positivo di percorrenza) e da una direzione n ortogonale a essa. Se x è l’ascissa del generico elemento della corda nella sua originaria configurazione rettilinea, e t è il tempo, lo spostamento trasversale s che istante per istante subisce l’elemento suddetto è una funzione di x e t, che, come si dimostra a partire dalla seconda legge della dinamica, deve soddisfare l’equazione alle derivate parziali del secondo ordine

[1] formula(

dove le costanti ρ e τ rappresentano rispettivamente la massa per unità di lunghezza, o densità lineica, della corda e la tensione), nonché a determinare condizioni al contorno, variabili da caso a caso (corda fissata rigidamente a un solo estremo, fissata elasticamente ai due estremi ecc.), e a determinate condizioni iniziali (posizione e velocità iniziale dei singoli punti della corda). Per soddisfare la [1], s dovrà risultare, per ogni elementino (o particella), piccolo di fronte alla lunghezza l della corda, ciò che si può tradurre nella condizione che il rapporto s/l sia abbastanza piccolo perché se ne possano trascurare le potenze superiori alla prima. La [1] è nota come equazione delle corde vibranti o equazione di d’Alembert; la più generale soluzione di essa è della forma (integrale di d’Alembert)

[2] formula,

dove s₁ e s₂ sono funzioni, a priori arbitrarie, degli argomenti x−vt e x+vt, e v è una costante, avente le dimensioni di una velocità, legata a τ e ρ dalla relazione

Da quest’ultima relazione segue che la [1] può anche essere scritta nella forma:

[3] formula.

O. progressive

Vediamo ora di renderci conto del significato delle due funzioni s₁ e s₂ che compaiono nella [2]. Consideriamo la prima di esse, s₁. Si tratta di una funzione il cui argomento è x−vt; questo argomento non si altera se si dà a t un qualunque incremento dt e al tempo stesso si incrementa x della quantità dx=vdt: infatti è (x + v dt) − v(t + dt) = x − vt.

Se quindi a un dato istante t̄ lo spostamento s₁ ha un certo valore s̄ in un punto x̄, all’istante successivo t̄+dt esso avrà lo stesso valore nel punto x̄+vdt, spostato rispetto a x̄ del trattino vdt nel verso delle x crescenti. Poiché ciò vale per ogni punto, la configurazione della corda all’istante t̄+dt sarà la stessa che all’istante t̄ ma traslata di vdt nel verso delle x crescenti. In altri termini, le cose vanno come se la configurazione assunta dalla corda a un dato istante si spostasse, mantenendosi inalterata, con una velocità di propagazione v nel verso positivo dell’asse x: s₁ rappresenta, con ovvia denominazione, un’o. progressiva permanente (o progressiva non smorzata). Secondo quanto premesso, si tratta di un’o. trasversale, in quanto le vibrazioni degli elementini della corda avvengono tutte secondo la direzione n ortogonale alla direzione di propagazione x: il piano xn, cioè il piano α della fig. 1, si chiama piano di vibrazione, mentre il piano β contenente x e normale al piano α si chiama piano di polarizzazione, e l’o. si dice polarizzata.

O. armoniche

Particolarmente semplice e importante è il caso delle o. armoniche o sinusoidali, caratterizzate dal fatto che la configurazione della corda, o, come si dice, il profilo d’o., è una sinusoide:

[4] s₁ = a sen[b(x − vt) + ϕ],

dove a, b, ϕ sono opportune costanti, delle quali a, che rappresenta lo spostamento massimo del generico elementino della corda dalla sua posizione d’equilibrio, ha il nome di ampiezza dell’onda. La quantità che costituisce l’argomento del seno, cioè b(x−vt)+ ϕ, da misurarsi in radianti, si chiama fase dell’o. nel punto di ascissa x e all’istante t; pertanto ϕ è la fase all’istante iniziale (t=0) nell’origine delle ascisse (x=0). Convenendo di indicare con λ l’intervallo di ascisse percorrendo il quale la fase dell’o. varia di 2π rad, si ha b=2π/λ, di modo che la [4] può porsi nella forma:

[5] formula,

ovvero, ponendo ulteriormente

[6] formula,

nella forma equivalente

[7] formula.

fig. 2A

Dal fatto che la funzione seno è periodica con periodo 2π rad, segue che s₁ è funzione periodica con periodo 1 della variabile (x/λ−t/T), cioè che essa è funzione periodica tanto di x quanto di t, rispettivamente con i periodi λ e T. Ciò significa che, se si fissa l’attenzione su un determinato valore di x, per la vibrazione trasversale del corrispondente elementino della corda si ha nel tempo un andamento sinusoidale (fig. 2A), con periodo T, che si chiama perciò periodo del moto ondoso in esame: si ha cioè uno stesso valore, s̄₁, per lo spostamento relativo a due istanti t ̄ e t ̄ + nT (con n intero non nullo) che differiscono tra loro di T o di multipli interi di T. Se invece si fissa l’attenzione su un determinato istante, l’andamento in quell’istante degli spostamenti trasversali delle varie particelle della corda, cioè il profilo dell’o., è anch’esso sinusoidale, con il periodo λ, che si chiama lunghezza d’o., in quanto se ci si muove lungo x di un tratto pari a λ o a un multiplo intero di λ (per es., da x̄ a x̄+λ; fig. 2B), gli spostamenti si riproducono identicamente. Com’è chiaro, a norma della [6] e della definizione data per λ, il periodo T rappresenta l’intervallo di tempo in cui l’o. percorre un tratto pari alla sua lunghezza d’o. λ e in cui la fase dell’o. varia di 2π rad; all’inverso del periodo, ν, si dà il nome di frequenza dell’o.:

[8] formula;

alla quantità

[9] formula,

che rappresenta, in rad/s, la variazione della fase dell’o. nell’unità di tempo, si dà il nome di pulsazione dell’o.; infine, l’inverso, k, della lunghezza d’o.,

[10] formula,

che rappresenta il numero (generalmente non intero) di lunghezze d’o. compreso nell’unità di lunghezza, si chiama numero di onde. Grazie alle grandezze ora introdotte, per rappresentare l’o. che si propaga lungo la corda nel verso positivo dell’asse x si possono usare le seguenti espressioni, equivalenti tra loro ed equivalenti alle [5], [7]:

È da notare che con una conveniente scelta dell’istante dal quale si comincia a misurare lo scorrere del tempo, ϕ può assumere un qualsivoglia valore: in particolare, si può ottenere che sia ϕ=0, oppure che la funzione seno venga sostituita dalla funzione coseno o che muti il segno dell’argomento. In certe questioni risulta poi comoda la rappresentazione complessa del moto ondoso, basata sull’osservazione che una qualunque delle espressioni prima date per s₁ può essere considerata, in virtù della formula di Eulero, come la parte reale di un’opportuna funzione complessa. Per es., alla [10] corrisponde la parte reale della funzione

s₁ = a exp{i[2π (kx − νt) +ϕ − π/2]},

essendo i²=−1; si può allora scrivere:

A è detta ampiezza complessa dell’o.: il suo modulo è l’ampiezza a dell’o., mentre il suo argomento cambiato di segno è la fase iniziale nell’origine. L’importanza delle o. armoniche deriva dal fatto che a esse ci si può in definitiva ricondurre in ogni caso. Per un teorema di Fourier, infatti, la funzione s che compare nella [2], anche se non periodica, può sempre scriversi come una sovrapposizione di funzioni sinusoidali, di modo che un’o. qualunque può sempre pensarsi come risultante dalla sovrapposizione di o. armoniche.

O. retrograde

Le stesse considerazioni sin qui svolte a proposito della funzione s₁(x−vt) possono essere ripetute a proposito della funzione s₂(x+vt), salvo che quest’ultima rappresenta un’o. che si propaga nel verso delle x decrescenti, cioè un’o. retrograda; anche per s₂ valgono, nel caso di o. armoniche, le espressioni date per s₁, salvo il segno contrario per il termine contenente la variabile temporale (+t/T in luogo di −t/T; +νt in luogo di −νt; ecc.). La presenza contemporanea nella [2] di una funzione rappresentante un’o. progressiva e di una funzione rappresentante un’o. retrograda è cosa che non deve stupire, dipendendo essa dalle particolari condizioni in cui si opera, ovvero, in termini analitici, dalle condizioni iniziali e al contorno da imporre nei vari casi all’equazione [1].

O. stazionarie

Un caso notevole di sovrapposizione dell’o. progressiva e dell’o. retrograda è quello che dà luogo alla formazione di o. stazionarie, caratterizzate dalla circostanza che certi punti della corda, detti nodi di vibrazione, in posizione fissa, restano in quiete, mentre in altri punti, detti ventri di vibrazione, anch’essi corrispondenti a particolari valori dell’ascissa x, l’ampiezza di vibrazione è massima: il profilo d’o. è quindi immobile. Il fenomeno si produce, per es., in corde di lunghezza finita, fissate agli estremi. Il corrispondente problema analitico consiste nel risolvere la [3] sotto la duplice condizione che sia, per qualunque valore di t, s=0 per x=0 e per x=l, convenendo di assumere l’origine delle x in un estremo e di indicare con l la lunghezza della corda nella sua configurazione d’equilibrio, rappresentata dall’asse x; una soluzione particolare è: s=asenpx sen(pvt+q), in cui a, p, q sono costanti da determinare in base alle condizioni al contorno (per x) e iniziali (per t). Imponendo le condizioni prima precisate per x si ha per la soluzione generale:

[11] formula,

fig. 3A

in cui r è un intero positivo, non nullo. Tale relazione mostra come nella corda si possano destare infinite o. stazionarie, ciascuna corrispondente a un valore di r, che hanno il nome di modi di vibrazione; a_r e ϕ_r, ampiezza e fase iniziale del modo r-esimo, risultano determinate in base alle condizioni iniziali, le quali per di più determinano anche quali sono i modi di vibrazione che effettivamente si destano nella corda. Che ciascun termine della [11] sia un’o. stazionaria risulta chiaramente dal fatto che nei punti la cui ascissa x vale nl/r, con n=0, 1, ..., r, l’ampiezza è nulla, cioè si hanno nodi, mentre nei punti di ascissa x=(2n+1) l/(2r), con n=0, 1, ..., r−1, l’ampiezza è massima e pari ad a_r, cioè si hanno ventri. Si ricava per la pulsazione del modo r-esimo il valore ω_r=rπv/l, e quindi per la frequenza il valore ν_r=rv/2l e per la lunghezza d’o. il valore λ_r=2l/r. Risulta così che per r=1 la frequenza ha il valore più basso possibile e la lunghezza d’o. è la massima possibile: è l’o. fondamentale, o prima armonica, corrispondente al fatto che la corda contiene una semilunghezza d’o., e che il punto di mezzo della corda è l’unico ventre (M in fig. 3A). Per r=2, 3, ... si hanno o. di frequenza doppia, tripla, ... rispetto a quella dell’o. fondamentale (seconda armonica, terza armonica, ...), di cui la corda contiene 2, 3, ... semilunghezze; per valori pari di r nel punto di mezzo M della corda cade un nodo (fig. 3 B), mentre per r dispari in M cade un ventre (fig. 3 C). La soluzione adatta al caso che si sta studiando si ottiene imponendo alla [11] le condizioni iniziali, cioè le condizioni che danno conto della posizione iniziale e della velocità iniziale di ogni punto della corda. Queste grandezze dipendono essenzialmente dal modo con cui la corda viene eccitata a vibrare. Per es., se la corda viene eccitata nel suo punto di mezzo, a_r risulta nulla per r pari, e inversamente proporzionale a r² per r dispari: la corda vibra essenzialmente sulla frequenza fondamentale. Il fatto che si possano determinare vibrazioni più o meno ricche di armoniche viene utilizzato in musica per gli strumenti a corda.

O. smorzate

Abbiamo sin qui considerato o. di ampiezza costante, ma in realtà la presenza di inevitabili resistenze passive (se non altro, la resistenza offerta dall’aria in cui la corda vibra) fa sì che le vibrazioni siano in genere smorzate. Come si sa dalla meccanica, ciò comporta la presenza di un termine contenente la derivata prima ∂s/∂t nella [3], la quale assume la forma:

[12] formula.

Come si dimostra, per un’o. armonica progressiva la soluzione è del tipo:

s = a exp(− αt/2) sen[b (x − vt) +ϕ],

dove a, b, ϕ sono costanti da determinare e 2/α è la costante di tempo dello smorzamento della vibrazione.

O. in un generico mezzo elastico

Come in una corda elastica, così in un generico mezzo elastico si possono determinare fenomeni ondosi. Precisamente, se in un punto di un sistema elastico (solido, liquido o aeriforme) si determina, per una causa qualsiasi, una perturbazione di preesistenti condizioni di equilibrio, generalmente tale perturbazione non si limita all’elemento in cui ha avuto origine, ma si trasmette agli elementi immediatamente vicini. Ciascuno di questi a sua volta lo trasmette agli elementi circostanti: la perturbazione si propaga così da un punto all’altro del sistema, in tutte le direzioni accessibili, con più o meno grande velocità. Il problema dinamico che si pone, in relazione alla propagazione di tale perturbazione, è ancora quello di determinare in funzione del tempo t lo spostamento (vettoriale) s del generico elementino del sistema, quando siano note le forze e assegnate le condizioni al contorno e iniziali (posizione e velocità) di ciascun elementino. Il problema si traduce in un sistema di tre equazioni differenziali alle derivate parziali del second’ordine nelle componenti cartesiane s_x, s_y, s_z di s, equazioni che subito si ottengono da quelle della statica elastica (➔ elasticità) sostituendo, a norma del principio di d’Alembert, alle forze attive le forze perdute.

O. elastiche irrotazionali

Nel caso delle o. elastiche irrotazionali, che si ha quando lo spostamento s è un vettore irrotazionale, ossia è rots=0, oppure, in termini equivalenti, s deriva da un potenziale ϕ, se si trascurano le resistenze passive, il moto è retto da un’equazione scalare che si può porre nella forma

[13] formula,

dove ∇2 è il laplaciano e v è la velocità di propagazione, legata alle costanti di Lamé, λ e μ, e alla densità ρ del mezzo (supposto omogeneo e isotropo) dalla relazione

[14] formula.

La [13] è dello stesso tipo della [1], e ad analoghe equazioni soddisfano le componenti dello spostamento s; quest’ultimo si ottiene, ovviamente, calcolando il gradiente di ϕ. Se ϕ dipende, oltre che dal tempo, da una soltanto delle tre coordinate spaziali, per es. dalla x, si ha:

[15] formula,

mentre le altre due componenti s_y e s_z di s risultano identicamente nulle. La soluzione generale della [15] è, naturalmente, dello stesso tipo della [2]

[16] s_x = s_x1(x − vt) + s_x2(x + vt),

dove s_x1, s_x2 sono funzioni determinabili in base alle condizioni al contorno e iniziali. Le superfici (o fronti) d’o., ognuna delle quali è il luogo dei punti in cui l’argomento della funzione rappresentante l’o. progressiva, x−vt, ha uno stesso valore (e analogamente per la funzione rappresentante l’o. retrograda), sono piani normali a x, in ciascuno dei quali lo spostamento, parallelo a x, ha ovviamente lo stesso valore: la [16] rappresenta o. irrotazionali piane longitudinali, la qualifica di piane riferendosi alla forma della superficie d’o. e quella di longitudinali al fatto che la vibrazione del generico elementino del mezzo avviene lungo la direzione di propagazione, x. Può anche darsi il caso che le superfici d’o. non siano piane.

Tra le o. non piane, particolare importanza hanno le o. sferiche, che si considerano quando la propagazione ondosa abbia simmetria sferica rispetto a un punto O: caso che effettivamente si ha quando la sorgente della perturbazione è puntiforme e il mezzo è omogeneo e isotropo. Il gradiente di ϕ dà lo spostamento s, e la divergenza di quest’ultimo dà la dilatazione (o compressione) volumica γ del mezzo; si ha dunque γ=divs=div gradϕ=∇²ϕ, e ciò significa che γ varia nello stesso modo con cui varia lo spostamento: corrispondentemente a spostamenti del generico elementino del mezzo da una parte e dall’altra rispetto alla posizione d’equilibrio, il mezzo si addensa e si rarefà, cioè nel mezzo medesimo si propagano o. di compressione e di dilatazione.

O. elastiche rotazionali

Sono o. che si producono in un mezzo elastico incomprimibile, in cui cioè si abbia γ=divs=0, essendo γ la dilatazione cubica e s lo spostamento del generico elementino del mezzo. Ponendo

[17] formula,

ove i simboli hanno il significato precedentemente indicato, si riconosce che lo spostamento deve soddisfare all’equazione vettoriale

,

che, proiettata sugli assi, dà luogo a tre equazioni formalmente analoghe a quelle che si hanno nel caso delle o. irrotazionali, ma rappresentanti un fenomeno di propagazione ondosa del tutto diverso. Lo spostamento, infatti, che nelle o. irrotazionali avviene lungo la direzione di propagazione, avviene ora perpendicolarmente a tale direzione: di qui la qualifica di o. trasversali. Inoltre, la velocità di propagazione, data dalla [17], è, a parità di ogni altra condizione, minore di quella delle o. irrotazionali, data dalla [14]. Analogamente al caso delle o. irrotazionali, può accadere che il fronte d’o. sia piano (o. piane trasversali) oppure sferico (o. sferiche trasversali); se in particolare la direzione di propagazione coincide con l’asse x del sistema cartesiano di riferimento, il caso delle o. piane corrisponde alla circostanza che s ha identicamente nulla la componente s_x (s è normale a x), mentre le componenti s_y e s_z dipendono unicamente da x e dal tempo t. In particolari condizioni può accadere che il rapporto s_x/s_y=tgϑ sia costante; ciò significa che s giace sempre nel piano (detto piano di vibrazione) contenente l’asse x e inclinato dell’angolo ϑ rispetto al piano xy: l’o. si dice polarizzata rettilineamente, e si chiama piano di polarizzazione di essa il piano contenente l’asse x e perpendicolare al piano di vibrazione. Se ϑ=0, s_z è identicamente nulla (il piano di vibrazione è il piano xy), mentre se ϑ=π/2, è identicamente nulla s_y (il piano di vibrazione è il piano xz). Il fenomeno della polarizzazione è esclusivo delle o. trasversali: esso cioè non può verificarsi per le o. longitudinali.

O. elastiche di tipo generale

Una generica o. elastica si può sempre considerare come dovuta alla combinazione di un’o. irrotazionale e di un’o. rotazionale; quel che v’è di importante è che essa, se permanente, è sempre rappresentata dall’equazione

[18] formula,

di cui in precedenza sono state esaminate varie forme particolari; a seconda delle circostanze, K può essere una grandezza scalare oppure una grandezza vettoriale, come pure, a seconda delle circostanze, variano le condizioni al contorno e iniziali, le quali in particolare determinano il ‘carattere’ dell’o., che può risultare progressiva o retrograda, oppure una combinazione di questi due tipi e in particolare stazionaria, e inoltre può risultare un’o. a una dimensione (com’è, per es., nel caso delle corde vibranti), a due dimensioni (per es., nel caso di membrane vibranti), a tre dimensioni (per es., o. longitudinali nell’aria); in quest’ultimo caso poi, in relazione alla forma del fronte d’o. si possono avere vari tipi di onde. La [18] si presta a descrivere onde di qualunque natura, anche non elastiche; per tale sua proprietà è denominata equazione delle o., o equazione del moto ondoso o equazione della propagazione per onde. In realtà, la [18] non rappresenta con piena generalità la propagazione per o.: essa si riferisce, come abbiamo a suo tempo precisato, a moti ondosi permanenti, non smorzati. A rigore, come equazione generale del moto ondoso va assunta la seguente:

,

che, mediante il termine α ∂K/∂t, dà conto di un eventuale smorzamento del moto e di cui la [12] costituisce la particolarizzazione nel caso delle corde elastiche vibranti.

È stato ricordato come un caso notevole di propagazione per o. sia costituito dalle o. armoniche, rappresentabili mediante funzioni sinusoidali. In effetti si tratta però di un caso piuttosto particolare, dato che in genere il profilo di un’o. non è sinusoidale, e l’o. medesima è rappresentabile come combinazione lineare di più o. armoniche, con ampiezza, frequenza e fase iniziale opportune. Poiché le grandezze da cui dipende la velocità di propagazione v non sono in genere indipendenti dalla frequenza, le varie componenti armoniche di un’o. non armonica si propagano con velocità diversa l’una dall’altra (fenomeno della dispersione) e il profilo dell’o. cambia di forma via via che l’o. avanza. Si deve allora distinguere tra la velocità v di propagazione di ogni componente dell’o., che chiameremo velocità di fase di quella componente, e la velocità u con cui procede l’o. nel suo insieme, che chiameremo velocità di gruppo; la velocità di fase di una componente è la velocità con cui avanza ogni fronte d’o. di quella componente, mentre u è la velocità di propagazione dell’energia associata all’o. (si tratta di un’energia ripartita tra le varie componenti). La relazione generale tra le due velocità è piuttosto complessa. Nel caso che le componenti siano di frequenza non molto diversa, vale la relazione (formula di Rayleigh):

,

in cui v è la velocità di fase dell’o. la lunghezza della quale è λ.

O. elastiche nei gas

In seno a un gas possono generarsi e propagarsi o. elastiche longitudinali. La trattazione di tali o. può farsi con riferimento allo spostamento s del generico elementino del mezzo oppure con riferimento al potenziale dello spostamento o della velocità di spostamento. Se ci si riferisce allo spostamento e si assume l’asse x coincidente con la direzione di propagazione, potremo considerare lo spostamento come una funzione scalare, s, di x e del tempo t, che deve soddisfare all’equazione

,

essendo p la pressione e ρ la densità. Queste due grandezze non sono indipendenti tra loro; precisamente, se il gas può essere assimilato a un gas perfetto e la frequenza delle o. è relativamente piccola, di modo che le compressioni e le dilatazioni del gas avvengano lentamente e siano assimilabili a trasformazioni isoterme, si ha

,

essendo k una costante caratteristica del gas in questione. Se invece la frequenza, come accade nella maggior parte dei casi, è relativamente grande, si può ritenere di essere in presenza di trasformazioni adiabatiche e si può scrivere:

[19] formula,

essendo γ il rapporto tra il calore specifico a pressione costante e il calore specifico a volume costante.

O. elastiche nei liquidi

fig. 4

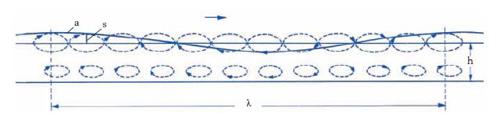
Anche nei liquidi, come è ben noto, si possono generare delle o., per azione del vento, di correnti, di corpi immersi ecc. Si può aggiungere anzi che, storicamente, sono state proprio queste o. (e in special modo quelle marine) a fornire modelli, immagini e nomi per la descrizione e lo studio degli altri fenomeni ondulatori. Si tratta generalmente di o. delle quali non è facile dare soddisfacenti ed esaurienti schematizzazioni matematiche, poiché la semplicità di queste mal si presta a riprodurre la complessità del fenomeno fisico: possono infatti aversi sia o. longitudinali e trasversali, interessanti l’intero volume liquido, sia o. quasi superficiali. Tra le o. suscettibili d’una semplice schematizzazione sono le cosiddette o. progressive permanenti: si tratta in sostanza di quei moti dei liquidi nei quali la forma della superficie libera, o pelo libero, si sposta senza subire modificazioni con una certa velocità di propagazione v costante. È, per es., il caso che si verifica in un canale, a fondo orizzontale e a pareti verticali, di lunghezza molto grande (teoricamente infinita), quando, essendo trascurabile rispetto all’accelerazione di gravità l’accelerazione verticale dei singoli elementini (o particelle) del liquido, ciascuno di essi compie, al progredire dell’o., piccole oscillazioni. Le o. progressive permanenti, se si esclude il caso dell’o. solitaria, sono periodiche, cioè il pelo libero è costituito da archi di curva uguali riproducentisi periodicamente a distanza costante λ (lunghezza d’o.); e fra esse vanno particolarmente ricordate le o. trocoidali di F.J. von Gerstner e le o. semplici o sinusoidali di G.B. Airy. Tali denominazioni derivano dalla forma del profilo del pelo libero, che è appunto una trocoide (o, più esattamente, una cicloide accorciata), in un caso, una sinusoide nell’altro. Altre sostanziali differenze tra i due tipi di o. sono: a) si hanno o. di Airy se la profondità h del liquido è molto minore di λ (di qui l’altra denominazione di o. di acqua bassa) e o. di Gerstner invece, se h>>λ (o. di acqua alta o profonda); b) nelle o. di Airy la perturbazione ondosa interessa tutta la sezione del liquido, mentre nelle o. di Gerstner la perturbazione non si estende molto al di sotto del pelo libero (o. superficiali). Per quanto riguarda le o. di Airy, se si indica con s (fig. 4), lo spostamento del generico elementino (o particella) del pelo libero dalla sua posizione d’equilibrio, assumendosi quest’ultima giacente nel piano xy e l’asse x normale alla sezione del canale, si trova che s deve soddisfare all’equazione

[20] formula,

con

g è l’accelerazione di gravità, mentre b e A, generalmente dipendenti da x, sono la larghezza al pelo libero e l’area della sezione verticale ‘liquida’ del canale. Se quest’ultima è rettangolare costante, si ha A=bh, essendo h la profondità del liquido, e per la velocità di propagazione si ha:

[21] formula.

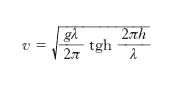
In generale, per la velocità v vale la relazione:

[22] formula.

Se h>>λ, è tgh(2πh/λ)≅1 e si ha v=(gλ/2π)^1/2 (formula di Gerstner); se invece è h<<λ, si ha tgh(2πh/λ)≅2πh/λ e per v si ottiene la [21]. La [22], che costituisce dunque una relazione abbastanza generale, da cui si possono derivare espressioni valide per o. sia di acqua alta sia di acqua bassa, è nota come formula di Airy. Sia le o. di Gerstner sia quelle di Airy sono modelli analitici, che trovano tuttavia largo impiego nelle applicazioni idrauliche e nautiche come base teorica per affrontare complessi problemi pratici.

O. elastiche nei solidi

Ancora più complesso rispetto al caso delle o. nei liquidi è quello delle o. che possono generarsi e propagarsi in un solido; si tratta di o. elastiche di tipo generale, cioè rotazionali o irrotazionali, che spesso si combinano in modi complicati. Le trattazioni analitiche di cui si dispone sono relative a casi particolari; tra questi vanno ricordati: a) il caso delle corde vibranti; b) il caso di membrane elastiche vibranti, la cui trattazione è per molti versi analoga a quella delle o. superficiali nei liquidi; c) il caso di sbarre elastiche, in cui, a differenza dei casi precedenti, si possono destare anche o. longitudinali, la cui trattazione è analoga, almeno formalmente, a quella delle o. in un gas racchiuso in un condotto; d) il caso di un mezzo semiinfinito, studiato da lord Rayleigh, sulla superficie del quale si possono destare o., dette o. di Rayleigh, consistenti in contemporanee vibrazioni trasversali e longitudinali, la cui energia è confinata in uno spessore dell’ordine di una lunghezza d’o. al di sotto della superficie limite del mezzo materiale (l’alta densità di energia elastica collegata con questo tipo di o. dà luogo a vistosi fenomeni di non linearità elastica, quali la generazione di armoniche e il mescolamento di frequenze); e) il caso di un mezzo stratiforme, compreso tra altri mezzi di diverse caratteristiche elastiche, nel quale possono insorgere o. di tipo speciale (o. di Love), trasversali, polarizzate, vibranti in un piano orizzontale, la cui propagazione, in particolare, può essere ristretta, in virtù di fenomeni di riflessione totale, allo strato in questione, che agisce come una sorta di guida per le o. medesime (o. canalizzate o guidate).

Tipi particolari di o. elastiche

fig. 5

O. acustiche

O. elastiche la cui frequenza è tale da eccitare sensazioni acustiche: precisamente, si tratta di o. la cui frequenza va da circa 16 a circa 20.000 Hz (➔ suono). O. di Alfvén Tipo di o. magnetoidrodinamiche (➔ magnetofluidodinamica). O. di discontinuità Con riferimento a un determinato fenomeno (precisamente a fenomeni che si traducano matematicamente in sistemi normali di equazioni alle derivate parziali), o. mediante le quali si propagano nello spazio certe discontinuità di qualche grandezza legata al fenomeno in esame. Si tratta di quei casi in cui esiste una superficie σ, mobile e generalmente deformabile nel tempo, tale che per una grandezza G legata al fenomeno si abbiano attraverso σ discontinuità nelle derivate parziali, a partire da un certo ordine, della funzione mediante la quale si esprime G (in modo che alle due facce di σ corrispondono determinazioni di G che soltanto parzialmente si raccordano attraverso σ e dalle due parti di σ valgono regimi diversi per la grandezza in esame) e le dette discontinuità si propaghino, al muoversi di σ, con andamento ondoso. Le o. di discontinuità sono dette più particolarmente o. ordinarie di discontinuità quando si debbano distinguere dalle o. d’urto. O. gravitazionali O. previste dalla teoria generale della relatività di A. Einstein, emesse da masse in moto, tali che il loro tensore di quadrupolo abbia derivata terza non nulla rispetto al tempo (➔ gravitazione). O. infrasonore O. longitudinali nell’aria, di frequenza minore di circa 16 Hz (➔ infrasuono). O di Rayleigh o superficiali Sono le onde che si propagano sulla superficie libera dei solidi e hanno interesse nelle applicazioni dell’elettronica e in teoria dei segnali. O. di Lamb Particolari eccitazioni ultrasoniche di tipo elastico di strutture laminari dei solidi; prendono il nome da H. Lamb e sono state utilizzate per l’analisi non distruttiva di materiali e sono quelle che interessano le perturbazioni di tipo sismico. O. di marea Con significato specifico, le o., progressive o stazionarie, che si stabiliscono in un fiume, o in un canale, per effetto delle oscillazioni di marea alla foce. O. sismiche O. elastiche longitudinali e trasversali che si propagano nella Terra dall’ipocentro di un terremoto. Le o. canalizzate si propagano in una stratificazione in cui la velocità di propagazione risulta inferiore sia a quella degli strati sottostanti sia a quella degli strati sovrastanti. Il nome è dovuto al fatto che, a causa delle suddette relazioni di velocità, le o. che tendono a uscire dalla stratificazione vengono rifratte verso l’interno di questa da parte sia degli strati inferiori sia di quelli superiori, per cui la stratificazione agisce come un canale che le convoglia. O. d’urto Nella meccanica dei fluidi, particolare o. di discontinuità, attraverso la quale la componente della velocità del fluido perpendicolare alla superficie d’o. subisce una variazione brusca. Un’o. d’urto può essere schematizzata come in fig. 5. La superficie d’o. σ (detta fronte d’urto) separa il fluido in due regioni: la regione a monte, indicata in figura come lato 1, e quella a valle, indicata come lato 2. Per semplicità, si è supposto che il fronte d’urto sia piano e che il fluido incida su di esso perpendicolarmente. In generale, non soltanto la velocità v, ma tutte le grandezze che caratterizzano il fluido (la densità ρ, la pressione p, la temperatura T, ...) variano in modo brusco attraverso il fronte d’urto. Questo, nella realtà, non è una superficie geometrica, ma uno strato assai sottile (avente uno spessore dell’ordine del cammino libero medio delle molecole), nel quale avvengono processi dissipativi responsabili delle variazioni dei parametri macroscopici del fluido. D’altra parte, le discontinuità delle varie grandezze, espresse dai rapporti v₂/v₁, ρ₂/ρ₁, p₂/p₁, ... (dove gli indici 1 e 2 si riferiscono alle due regioni del fluido definite in fig. 5), non sono arbitrarie. Occorre, infatti, che i valori di v₁, v₂, ρ₁, ρ₂, p₁, p₂, ... siano tali da rispettare le leggi di conservazione della massa, dell’energia e della quantità di moto. Queste impongono che i flussi di massa, di energia e di quantità di moto che ‘entrano’ nella superficie σ (dal lato 1) siano uguali a quelli corrispondenti che ne ‘escono’ (dal lato 2). Ne deriva che la velocità del fluido diminuisce passando dal lato 1 al lato 2 (v₁>v₂): più precisamente, si trova che la velocità del fluido deve essere supersonica a monte del fronte d’urto (v₁>c₁, essendo c₁ la velocità del suono sul lato 1) e subsonica a valle di questo (v₂<c₂, essendo c₂ la velocità del suono sul lato 2). Per la conservazione della massa, la disuguaglianza v₁>v₂ implica l’altra: ρ₁<ρ₂ (cioè il fluido attraversando il fronte d’urto subisce una compressione).

fig. 6

fig. 7

Un’o. d’urto si genera quando un flusso supersonico (➔ aerodinamica) incontra un ostacolo. Tale situazione si presenta, per es., nel caso di un aereo in volo supersonico (infatti, in un sistema di riferimento solidale con l’aereo, è l’aria a investire questo con velocità supersonica). La fig. 6 illustra schematicamente il fenomeno. Si supponga che l’aereo negli istanti successivi t₀, t₁, t₂, t₃, t₄, t₅ si trovi nelle posizioni P₀, P₁, P₂, P₃, P₄, P₅. In ciascun istante, esso perturba l’aria generando impulsi di onde sonore che si propagano in tutte le direzioni. Tuttavia, poiché l’aereo si muove alla velocità v, maggiore della velocità del suono c, le onde rimangono ‘indietro’ rispetto a esso. All’istante t₅, i fronti delle onde generate nei punti P₀, P₁, P₂, P₃, P₄, P₅ sono le superfici sferiche tratteggiate in figura, i cui raggi misurano rispettivamente r₀=c(t₅−t₀), r₁=c(t₅−t₁), ...: queste inviluppano una superficie conica, detta cono di Mach, il cui vertice cade nel punto P₅. Si trova che le o. sonore interferiscono positivamente (cioè si rafforzano a vicenda) lungo la superficie del cono di Mach, sviluppando, appunto, un’o. d’urto (il cosiddetto boom supersonico). Analogo è il caso dell’o. balistica, prodotta da un proiettile in moto supersonico attraverso l’aria. O. d’urto possono anche svilupparsi da o. sonore di ampiezza finita. Queste, infatti, si propagano attraverso un fluido, rimanendo inalterate, soltanto se hanno ampiezza infinitesima: se, invece, la loro ampiezza è finita, evolvono progressivamente trasformandosi in o. d’urto. Il fenomeno è illustrato nella fig. 7, che mostra le variazioni spaziali della densità ρ del fluido, intorno al valore medio ρ̄, in tre momenti successivi. Inizialmente ρ varia sinusoidalmente (fig. 7A). Tuttavia, la regione dove il fluido è compresso (ρ>ρ̄) viaggia più velocemente di quella dove esso è rarefatto (ρ<ρ̄) . Ciò perché la velocità di propagazione delle o. sonore aumenta con la densità: dalle equazioni [19] si ricava infatti c=(k′γρ^γ-1)^1/2. Ne segue che la regione di compressione tende a sopravanzare quella di rarefazione che la precede: la variazione di densità diventa pertanto sempre più brusca (fig. 7B) fino a dar luogo a una discontinuità, cioè a un’o. d’urto (fig. 7C).

O. elettromagnetiche

Le o. elettromagnetiche sono o. che si destano in un mezzo materiale o nel vuoto, generate da cariche elettriche accelerate; la perturbazione ondosa è sempre costituita da un campo elettrico e da un campo magnetico, variabili nel tempo. Tale perturbazione si propaga tutt’intorno nel mezzo sotto forma di o. che convogliano energia elettromagnetica. Chiamando sorgente la zona in cui è prodotta la perturbazione iniziale, potremo anche dire che le o. elettromagnetiche sono perturbazioni di carattere ondoso dello stato elettrico e magnetico del mezzo, mediante le quali si propaga la radiazione elettromagnetica irraggiata dalla sorgente; precisamente, le o. elettromagnetiche sono costituite da un campo elettrico e da un campo magnetico i cui vettori E, H sono, punto per punto e istante per istante, ortogonali tra loro e ortogonali alla direzione di propagazione; si tratta, dunque, di o. trasversali. Il punto di partenza per la trattazione delle o. elettromagnetiche è il complesso delle equazioni di Maxwell dell’elettromagnetismo. Poiché la risoluzione delle equazioni di Maxwell è in generale tutt’altro che semplice, ci limiteremo qui a considerare il caso che il mezzo sia omogeneo e isotropo: precisamente, considereremo prima un dielettrico perfetto e poi un mezzo conduttore.

O. elettromagnetiche in un dielettrico perfetto, omogeneo, isotropo

Per un mezzo del genere la conducibilità elettrica è ovunque, esclusa la sorgente, uguale a zero, mentre la costante dielettrica assoluta ε e la permeabilità magnetica assoluta μ sono costanti; supporremo per di più che nel mezzo non vi siano cariche elettriche localizzate, di modo che ovunque, esclusa la sorgente, sia zero la densità di carica libera; quindi le equazioni di Maxwell si scrivono:

[23] formula.

Applicando l’identità vettoriale

rot(rotE)=grad(divE)−∇2E

alla terza equazione e tenendo conto della prima e della quarta equazione, si ha:

[24] formula;

procedendo analogamente per H, si ottiene:

[25] formula.

Queste equazioni sono particolarizzazioni dell’equazione del moto ondoso: esse rappresentano dunque un campo elettrico e un campo magnetico, che si propagano per o. permanenti, la cui velocità (di fase) è

Le [24], [25], proiettate sugli assi di un sistema cartesiano di riferimento, danno luogo a due terne di equazioni scalari nelle componenti dei vettori E, H. Particolarmente interessante è il caso che si consideri una zona, non troppo estesa, abbastanza distante dalla sorgente della perturbazione; se si assume come asse x la semiretta che dalla sorgente passa per un punto P di tale zona, a un dato istante la determinazione di E e H è, con ottima approssimazione, la medesima in tutti i punti di un intorno di P giacenti sul piano normale all’asse x per P: si hanno cioè o. elettromagnetiche piane. Come senza difficoltà si riconosce, E e H risultano ortogonali tra loro e ortogonali all’asse x. Tale risultato è importante, in quanto ci assicura che le o. elettromagnetiche sono, in questo come in ogni altro caso, trasversali. In particolare, può accadere (o. piane polarizzate linearmente) che E e H siano sempre diretti secondo direzioni immutabili, ortogonali tra loro; ciò significa che, con un’opportuna rotazione del riferimento intorno all’asse x, è sempre possibile ridursi, in tale caso particolare, a due sole espressioni scalari

[26] formula

fig. 8

esprimenti il fatto che (fig. 8) E è sempre contenuto nel piano xy (piano di vibrazione) e H è sempre contenuto nel piano xz (piano di polarizzazione). E e H variano, nello spazio e nel tempo, con la stessa legge; tra le loro componenti esiste infatti una relazione di proporzionalità, che, nel caso delle [26], è la seguente: E_y=ZH_z, essendo

la cosiddetta impedenza caratteristica del mezzo. Tenendo presente che è ε=ε₀ε_r e μ=μ₀μ_r, essendo ε₀ e μ₀ la costante dielettrica e la permeabilità magnetica del vuoto e ε_r, μ_r le corrispondenti grandezze relative del mezzo, se si indica con c la velocità di propagazione delle o. nel vuoto, si ha:

[27] formula.

Se, come generalmente accade per i dielettrici, μ_r è poco diverso dall’unità e si tiene conto del fatto che

,

tali relazioni si semplificano, assumendo la forma:

Ricordiamo che ε_r è in generale una funzione piuttosto complicata della frequenza del campo elettrico: ciò significa che, in generale, la velocità di propagazione varia al variare della frequenza dell’o., cioè si ha dispersione (un’o. non armonica si deforma propagandosi), come anche varia l’impedenza caratteristica.

L’intensità energetica dell’o., I, è definita, come nel caso delle o. elastiche, quale energia che fluisce nell’unità di tempo attraverso una superficie di area unitaria, ortogonale alla direzione di propagazione. Le modalità della propagazione dell’energia elettromagnetica convogliata dall’o. sono efficacemente sintetizzate dal vettore di Poynting P=E×H; tale vettore dà con il suo orientamento la direzione e il verso di propagazione dell’energia e con il suo modulo l’intensità istantanea dell’o., sicché il valor medio di ∣P∣ dà l’intensità energetica I.

Come già accennato parlando delle o. elastiche di tipo generale, anche nel caso delle o. elettromagnetiche accade che se il mezzo è dispersivo (e tutti i mezzi materiali lo sono) e l’o. non è armonica, ogni componente dell’o. si propaga con una propria velocità (di fase) v, data dalla prima delle [27], mentre l’energia convogliata dall’o. si propaga con la velocità di gruppo, u, dell’o. in questione. Le due velocità coincidono se l’o. è armonica ovvero se, essendo l’o. qualunque, il mezzo è praticamente non dispersivo, qual è, tipicamente, il vuoto. La velocità di propagazione delle o. elettromagnetiche nel vuoto, c, correntemente, ma restrittivamente, detta anche velocità della luce nel vuoto, è una delle costanti fondamentali della fisica e il suo valore, quale risulta da esperienze di ottica (➔ luce) e da misurazioni elettromagnetiche, è c=299.792.458,0 m/s. In realtà, nel SI di unità di misura il metro (m) viene definito come la frazione 1/299.792.458,0 del percorso fatto dalla radiazione elettromagnetica in un secondo nel vuoto.

Dalle equazioni di Maxwell, in accordo con l’esperienza, discende che le sorgenti del campo elettromagnetico vero e proprio, cioè quello di radiazione, sono le cariche elettriche in moto con accelerazione vettoriale non nulla. Questo risultato è estremamente importante, in quanto equivale ad affermare che ogni carica elettrica animata di moto con accelerazione (vettoriale) non nulla irradia nello spazio circostante energia che si propaga per o. elettromagnetiche; precisamente, la potenza elettromagnetica irraggiata da una carica q che si muove con accelerazione a vale q²a²(εμ³)^1/2/3π. La frequenza delle o. elettromagnetiche è identica alla frequenza del moto delle cariche (se il moto non è di tipo armonico, le frequenze emesse sono quelle dei moti armonici dalla cui composizione, con i metodi della sintesi armonica, risulta il moto dato). In realtà, però, tale identità viene meno quando si considerano sistemi atomici e subatomici, ai quali non è più applicabile la fisica classica che va sostituita con la meccanica e l’elettrodinamica quantistica. In particolare, negli atti elementari di emissione e di assorbimento della radiazione elettromagnetica da parte degli atomi (ai quali è associata la transizione di un elettrone atomico tra due livelli energetici), si manifesta il comportamento corpuscolare della radiazione medesima, descrivibile in termini di quanti di energia elettromagnetica o fotoni, ciascuno dei quali possiede un’energia hν, una quantità di moto hν/c (essendo h la costante di Planck e ν la frequenza della radiazione) e quindi una massa a riposo uguale a zero. Cioè anche per la radiazione elettromagnetica si manifesta il dualismo o.-corpuscolo che caratterizza tutti i costituenti elementari della materia.

La tradizionale classificazione schematica dello spettro delle o. elettromagnetiche è la seguente: a) o. hertziane o radioonde: frequenza da qualche Hz a circa 10¹² Hz; si originano da moti non uniformi di cariche libere e, in particolare, da correnti elettriche variabili; in quest’ultimo caso, trattandosi di una corrente di conduzione originata dal moto ordinato di portatori di cariche, la radiazione è costituita da o. elementari (una per ciascun portatore di carica), persistenti se il moto è permanente e aventi tutte la stessa composizione armonica, cioè tutte costituite dalle stesse componenti armoniche: si tratta cioè di una radiazione coerente, caso che, eccezion fatta per la radiazione emessa dai laser, non si verifica per altre radiazioni elettromagnetiche, intrinsecamente incoerenti; b) o. infrarosse: frequenza da circa 10¹² Hz a 4,5∙10¹⁴ Hz (limite inferiore del colore rosso); si originano da vibrazioni molecolari e, limitatamente a quelle di frequenza più alta, anche da transizioni elettroniche relative a orbite esterne; c) o. luminose: frequenza da 4,5∙10¹⁴ Hz (limite inferiore del colore rosso) a 7,5∙10¹⁴ Hz (limite superiore del colore violetto); si originano da transizioni elettroniche relative a orbite esterne; d) o. ultraviolette: frequenza da 7,5∙10¹⁴ Hz (limite superiore del colore violetto) a circa 10¹⁶ Hz; si originano da transizioni elettroniche relative a orbite esterne; e) raggi X: frequenza maggiore di circa 10¹⁶ Hz; si originano da transizioni elettroniche relative a orbite interne e, per le frequenze più alte, anche da transizioni nucleari; f) raggi γ: frequenza maggiore di circa 10¹⁹ Hz; si originano da transizioni nucleari. Tale ripartizione dello spettro delle o. elettromagnetiche è molto schematica perché non sono nettamente definiti (tranne che per le o. luminose) i limiti tra un campo e l’altro, anche perché i meccanismi di emissione sono ripartiti in maniera più complessa di quella sopra delineata. Molto spesso per identificare un’o. elettromagnetica, o un campo di o. elettromagnetiche, ci si riferisce non alla frequenza ν ma alla lunghezza d’o. λ nel vuoto (λ=c/ν).

Onde hertziane

Con specifica denominazione, la qualifica di hertziane, talvolta usata come sinonimo di elettromagnetiche, è data alle o. elettromagnetiche (dette anche radioonde) che, in ragione della loro frequenza, possono essere generate con oscillatori elettrici e irradiate con antenne oppure trasmesse con altri adatti mezzi (cavi coassiali, guide d’o.), così da poter essere usate in sistemi di telecomunicazione (propriamente, sistemi di radiocomunicazione). La loro esistenza, teoricamente prevista da J.C. Maxwell, fu sperimentalmente dimostrata da H. Hertz (1887); lo stesso Hertz e poi altri studiosi, tra cui specialmente A. Righi, ne studiarono le caratteristiche e le modalità di propagazione, risultate identiche o quanto meno analoghe a quelle, ben note, della luce: riusciva così provata l’esattezza delle vedute maxwelliane sull’identità di natura di tutte le radiazioni elettromagnetiche. All’inizio del 20° sec., le o. hertziane furono applicate, essenzialmente a opera di G. Marconi, per realizzare comunicazioni a distanza: nasceva così un importante capitolo della tecnica delle comunicazioni e dell’elettronica, la radiotecnica, tuttora in rapido sviluppo (➔ radiocomunicazione).

tab.

La classificazione internazionale delle o. hertziane viene fatta in vari campi d’o., a seconda della lunghezza o della frequenza: o. miriametriche, metriche ecc.; o. a bassa frequenza, ad altissima frequenza ecc.: tali campi d’o. sono indicati con la sigla della denominazione inglese (per es., le o. a bassissima frequenza sono indicate come o. VLF, dall’inglese very low frequency). È anche possibile classificare le o. elettromagnetiche in bande di frequenze, ciascuna indicata con un numero, n, e relativa alle o. la cui frequenza sia compresa fra 0,3∙10ⁿ e 3∙10ⁿ Hz: così, per es., la banda 7 comprende le o. di frequenza fra 0,3∙10⁷ e 3∙10⁷ Hz, cioè fra 3 e 30 MHz (v. tab.).

Le principali specificazioni del termine o. in radiotecnica e nelle telecomunicazioni sono le seguenti: o. convogliate, utilizzate nei sistemi di telecomunicazione a frequenza vettrice, così dette in quanto la loro propagazione si fa avvenire su linee (per es., su linee di distribuzione dell’energia elettrica); o. guidate, quelle che si propagano in una guida d’o.; o. laterali, le varie o., simmetriche rispetto all’o. portante, che si producono nel processo di modulazione; o. portante, l’o. utilizzata, previa modulazione, per la trasmissione di segnali; o. smorzate, quelle nelle quali l’ampiezza delle oscillazioni decresce con continuità secondo una certa legge; o. superficiali (o dirette o di terra), o. che, partendo dal trasmettitore, raggiungono il ricevitore propagandosi lungo la superficie terrestre, cioè senza aver subito riflessioni, rifrazioni o diffusioni nella ionosfera o nella troposfera; o. troposferiche, o. che raggiungono il ricevitore in virtù di fenomeni di diffusione nella troposfera.

Altri impieghi e accezioni del termine onda

L’o. coniugata in fase (o invertita nel tempo) di un’o. propagantesi in un certo verso è un’o. che si propaga in verso opposto e la cui ampiezza complessa è il complesso coniugato dell’ampiezza dell’o. considerata (➔ ottica).

In radiotecnica, si hanno o. TE, o. TM, o. TEM, caratteristiche delle guide d’o. (➔ guida). Forma d’o. Lo stesso che profilo d’o., cioè diagramma della grandezza caratteristica dell’o. in funzione del tempo o del cammino: si parla così di forme d’o. sinusoidali, rettangolari, impulsive ecc. Funzione d’o. Funzione che descrive l’ampiezza di probabilità di un fenomeno quantistico, la cui evoluzione è retta dall’equazione di Schrödinger (➔ meccanica). Pacchetto (o gruppo) d’o. Perturbazione ondosa (elastica, elettromagnetica o anche di probabilità) interessante, istante per istante, una regione le cui dimensioni sono piccole rispetto ad altre lunghezze che compaiono nel problema che si sta studiando, ma grandi peraltro rispetto alla lunghezza d’o.; si può pensare costituita da un treno relativamente breve di oscillazioni, il cui inviluppo ha forma assegnata. Per es., un pacchetto d’o. hertziane può essere ottenuto inviando in un’antenna un impulso di corrente ad alta frequenza. Vettore d’o. Nella propagazione di un’o. armonica piana di lunghezza λ, il vettore il cui modulo è pari a 2π/λ (cioè a 2π volte il numero d’o.) e la cui direzione è quella di propagazione dell’onda.

In meccanica ondulatoria, il vettore d’o. k associato a una particella libera con quantità di moto p, per la relazione di de Broglie λp=h (con h costante di Planck), è dato da k=2πp/h.

Medicina

Espansioni e movimenti attivi di organi o loro parti: o. sfigmica, la ritmica espansione delle pareti arteriose per effetto della sistole cardiaca; o. peristaltiche, i movimenti intestinali (➔ peristalsi).

Salienze o depressioni nei tracciati della registrazione grafica di fenomeni meccanici o elettrici; per es.: o. P, Q, R, S, T dell’elettrocardiogramma (➔ elettrocardiografia); o. alfa, beta, delta dell’elettroencefalogramma (➔ elettroencefalografia) ecc.