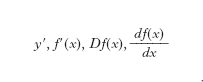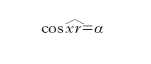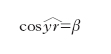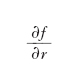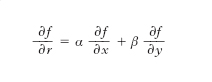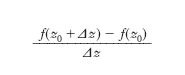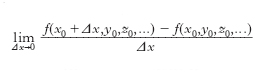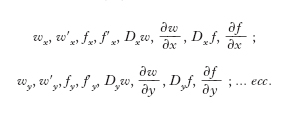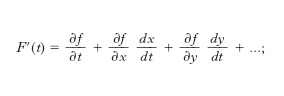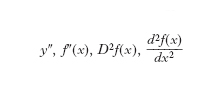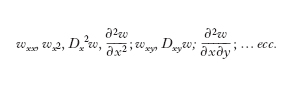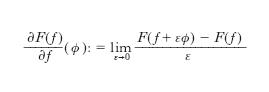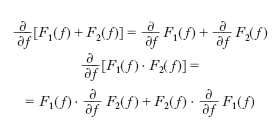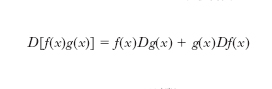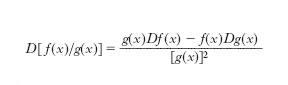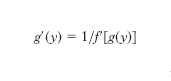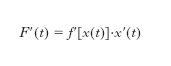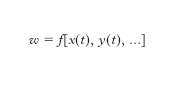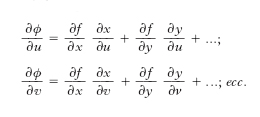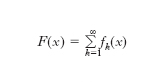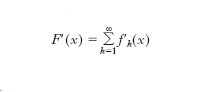derivata

tab.

Concetto fondamentale nell’analisi matematica e nelle sue applicazioni che esprime, date due grandezze l’una funzione dell’altra (per es., in fisica, lo spazio percorso e il tempo impiegato a percorrerlo, o anche, in economia, il prodotto ottenuto al variare della quantità di fattori di produzione impiegati ecc.), il modo di variare istantaneo di una grandezza rispetto all’altra (v. tab.).

In matematica, si dice d. di una data funzione reale f(x) in un punto x₀ che appartenga al campo di definizione di f(x) e ne sia punto di accumulazione, il limite (ove esista) del rapporto incrementale,

fig.

al tendere a zero dell’incremento Δx della variabile indipendente. La d. in x₀ è dunque un numero che rappresenta la maggiore o minore rapidità con cui varia la f(x) al variare di x in un intorno di x₀. Geometricamente, la d. di f(x) nel punto x₀ interno al suo intervallo di definizione (a, b) è il coefficiente angolare della tangente t alla curva y=f(x) nel punto di ascissa x₀. Dal grafico della funzione (v. fig.) risulta immediatamente che tg β è uguale al rapporto incrementale; al tendere di Δx a zero, P tende a P₀, la corda P₀P tende alla posizione della tangente, e tg α, come limite di tg β, risulta uguale alla d. di f(x) per x=x₀.

Nell’insieme dei punti in cui la f(x) è definita e ammette d. nasce una nuova funzione, definita come quella che in ognuno di tali punti assume il valore della d. di f(x); essa si chiama funzione d. della f(x), o semplicemente d. prima della f(x), e si indica con una delle seguenti notazioni:

Ove in un punto x_o non esista il limite del rapporto incrementale, cioè la d., esistono certo il massimo e il minimo limite di tale rapporto, e si chiamano rispettivamente massima e minima derivata. In questa ipotesi (che è la più generale) può accadere in particolare che esista e sia finito il limite del rapporto incrementale per Δx tendente a zero per valori positivi o per valori negativi; si parla allora di d. destra o di d. sinistra. Se la f(x) rappresenta una grandezza fisica, la sua d. ha spesso un notevole significato fisico: per es., se s=s(t) rappresenta l’equazione oraria del moto di un punto, la d. s′(t), che si indica anche con ṡ(t), ne rappresenta la velocità istantanea in funzione del tempo.

Tipologie di derivate

D. direzionale Data una funzione reale f(x, y), delle due variabili x, y, sia P₀ (x₀, y₀) un punto interno al campo di definizione C della funzione e sia r una retta per P₀, di coseni direttori formula,

formula,

si dice d. direzionale di f(x, y) nella direzione di r, o rispetto a r, e si indica con formula,

la quantità

Essa rappresenta la d. della funzione di una variabile che si ottiene considerando la f(x, y) come funzione del punto variabile sopra la retta r. D. di una funzione di variabile complessa Si definisce sostanzialmente come per le funzioni di variabile reale. Se z è la variabile complessa, la funzione f(z) si dice derivabile in senso complesso (anche olomorfa o monogena o analitica) nel punto z₀ interno al campo di definizione, se esiste il limite del rapporto incrementale

comunque tenda a zero l’incremento Δz (Δz può tendere a zero in più modi).

D. logaritmica D. logaritmica di una funzione f(x) è la d. della funzione log f(x)

D. parziale Assegnata una funzione w = f(x, y, z,...), reale, di m variabili, e fissato un punto interno al suo campo di definizione P(x₀, y₀, z₀, ...), si chiama d. parziale (in contrapposto alla d. ordinaria che è quella sopra definita per funzioni di una sola variabile) della funzione rispetto alla variabile x la d. (ove esista) della funzione f(x, y₀, z₀,...) della sola x, che si ottiene fissando i valori y=y₀, z=z₀, ... delle altre variabili e lasciando variare la x; in altre parole, tale d. è data da

Analogamente si definiscono le d. parziali rispetto alle altre variabili. Ciascuna di tali d. parziali è quindi una funzione delle variabili x, y, z,... e si chiama anch’essa d. parziale ( prima, in contrapposizione alle d. parziali successive).

Le d. parziali si indicano con i simboli

D. totale Se w=f(t, x, y, ...) è una funzione delle variabili t, x, y, ... e se x, y, ... sono a loro volta funzioni di t, w risulta in definitiva funzione della sola t: ossia w=F(t); la derivata di questa funzione si dice d. totale della funzione w ed è data da

la d. totale è pertanto la derivata della w, tenendo conto della sua dipendenza da t sia direttamente, sia attraverso x, y, z,... (➔ anche oltre, derivazione delle funzioni composte).

D. successive Data una funzione reale y=f(x) e considerata (ove esista) la sua funzione d. (prima) f′(x), tale funzione può ammettere una propria d. (prima), che si dice d. seconda della funzione di partenza, e si indica con

La d. della d. seconda si dice d. terza, e così la d. della d. (n−1)-esima si dice d. n-esima o d. di origine n e si indica con

D. successive parziali Data una funzione w=f(x, y, z,...), reale, di m variabili si considerino, ove esistano, le sue m d. parziali rispetto alle diverse variabili: w_x, w_y, …; ciascuna di esse, in quanto funzione di x, y, z,... può ammettere le d. parziali rispetto a ciascuna delle m variabili, e queste si dicono le d. parziali seconde della funzione data, e si indicano con i simboli

(o con notazioni analoghe) e si leggono rispettivamente: d. parziale seconda rispetto a x due volte (il primo gruppo); d. parziale seconda rispetto a x e a y (il secondo gruppo) ecc.; complessivamente le d. parziali seconde sono in numero m². Ciascuna di esse può ammettere le d. parziali rispetto a ciascuna delle variabili (d. parziali terze della funzione data, in numero di m³); e così via; le d. parziali n-esime (d. delle d. (n−1)-esime) sono mⁿ e si indicano per es. con la notazione

(essendo α+β+γ+...+λ+μ+ν+…=n). Ove valga il teorema di invertibilità dell’ordine delle derivazioni parziali, le d. di ordine n sono

D. funzionale Estensione dell’operazione di derivazione al calcolo funzionale, molto utilizzata nelle moderne applicazioni della fisica teorica e della teoria quantistica dei campi. Se si indica con F(f) un funzionale continuo definito su uno spazio di funzioni I, la sua d. funzionale ∂F/∂f rispetto alla funzione f(x) è il funzionale definito dalla relazione

dove ϕ ∈ I è una generica funzione. In fisica teorica si usa la notazione ∂F(f)/ ∂f(ϕ)=ʃ∂F(f)/∂f(y) ϕ(y)dy, dove ∂F(f)/∂f(y) è una distribuzione. Tra le proprietà algebriche della d. funzionale:

Regole di derivazione

Le regole di derivazione permettono di calcolare la d. di una funzione, costruita mediante altre funzioni, note le d. di queste ultime. Diamo in formule le regole di derivazione fondamentali.

Derivazione di una combinazione lineare: se λ₁, λ₂ ,..., λ_n sono costanti,

formula

Derivazione di un prodotto:

Derivazione di un quoziente:

(valida per i valori di x tali che g(x)≠0). S’intendono naturalmente esistenti nel punto x tutte le d. che compaiono nelle formule considerate. Le regole valgono anche per le funzioni di più variabili pur di convenire che D indichi una determinata operazione di derivazione parziale, rispetto ad alcune determinate variabili.

Derivazione della funzione inversa Se la funzione y=f(x) è derivabile in un intervallo (a, b) e ivi la sua d. è sempre positiva o sempre negativa, essa è dotata di funzione inversa x=g(y), tale cioè che in tutto (a, b) risulta x=g[f(x)]. In tal caso la d. della x [concepita come funzione della y nell’intervallo descritto da y=f(x) al variare di x in (a, b)] è espressa da:

Derivazione delle funzioni composte Se si ha una funzione, y=f(x), della x e questa a sua volta è funzione di una variabile t, x=x(t), la y risulta funzione di t, y=F (t) =f[x(t)]; risulta in tal caso:

purché esistano nel punto t e nel punto x(t) le d. rispettivamente della x(t) e della f(x). Più in generale se w=f(x, y,...) è una funzione di x, y,... e se x=x(t), y=y(t), ... sono funzioni della variabile t,

risulta una funzione w=F(t) della sola t; la d. F’ di tale funzione coincide con la sua d. totale. Se poi x=x(u, v, ...), y=y(u, v, ...) sono funzioni delle variabili u, v, ..., allora per la funzione w si ha w=f[x (u, v, ...), y (u, v, ...)], cioè, in definitiva, la w risulta essere una funzione ϕ delle u, v,... : w=ϕ (u, v,...); le d. parziali di tale funzione sono:

Derivazione per serie Se in un intervallo (a, b) si ha

cioè se la funzione F(x) è somma di una serie data, se le funzioni f_k(x) sono derivabili in (a, b) e se la serie delle d. è uniformemente convergente, la somma di quest’ultima serie è la funzione d. di F(x), cioè

Invertibilità delle derivazioni parziali Se una data funzione dipende da due o più variabili ed è derivabile rispetto a ciascuna di esse vale un teorema di invertibilità dell’ordine delle derivazioni parziali: per es., per una funzione di due variabili, f(x, y), nell’ipotesi che esistano le d. f′_x, f′_y, f″_xy nell’intorno di un punto P e che f″_xy sia continua in P, è assicurata l’esistenza della derivata parziale seconda f″_xy e si ha f″_xy=f″_yx.

Funzioni derivabili Una funzione che ammetta d. in un punto, in un intervallo ecc., si dice ivi derivabile. Si dimostra che se una funzione è derivabile in un punto, essa è ivi anche continua. Non è vera però la proposizione reciproca: K. Weierstrass, per primo (1872), ha fornito un esempio di funzione continua non derivabile. Di notevoli importanza, soprattutto per lo studio di massimi e minimi, sono alcuni teoremi sulle funzioni derivabili in un intervallo. Siano f(x) e g(x) due funzioni continue in un intervallo chiuso [a,b] e derivabili nell’intervallo aperto (a,b), allora si applicano i teoremi seguenti.

Teorema di Rolle: se f(x) assume valori uguali in a e b, esiste almeno un punto interno all’intervallo in cui si annulla la d. prima della f(x).

Teorema di Cauchy: esiste almeno un punto ξ di (a,b) per il quale si ha g′(ξ) [f(b)−f(a)]=f′(ξ) [g(b)−g(a)].

Teorema di Lagrange: esiste almeno un punto ξ di (a,b) per il quale si ha f(b)−f(a)=(b−a) f′(ξ).