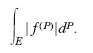somma

somma In matematica, il risultato dell’ordinaria operazione di addizione o anche l’operazione stessa; in senso estensivo, si parla spesso di s. anche con riferimento a operazioni che soddisfano le proprietà formali dell’addizione ordinaria, o anche solamente alcune di esse. S. algebrica S. di numeri positivi o negativi, o anche s. di quantità algebriche. S. diretta di spazi vettoriali V1, ..., Vk è lo spazio vettoriale V, denotato con il simbolo V1 ⊕ ... ⊕ Vk, tale che ogni vettore v di V si possa esprimere nella forma v1+ ... + vk, con v1 ∊V1, ..., vk ∊ Vk, e inoltre che tale rappresentazione sia unica. Se gli spazi V1,..., Vk hanno dimensioni, rispettivamente, d1,..., dk, la dimensione di V è uguale a d1 + ... + dk. In modo simile si definisce la s. diretta di A-moduli, di algebre ecc. S. logica Nelle algebre di Boole, operazione corrispondente all’usuale operazione logica di congiunzione. Con significato simile, in elettronica, operazione logica elementare su due o più variabili binarie il cui risultato è nullo se e solo se sono contemporaneamente nulli tutti gli addendi.

In analisi matematica, funzione sommabile, sinonimo di funzione integrabile: una funzione f(P) a valori reali, definita su un insieme E⊂Rn, si dice sommabile in E se ha valore finito l’integrale

Esistono vari criteri per stabilire se una funzione sia o no sommabile. Alcuni di questi si applicano alle funzioni illimitate e ne considerano l’eventuale ordine di infinito; altri si applicano a funzioni definite su insiemi E illimitati, e ne considerano l’eventuale ordine di infinitesimo. Le funzioni sommabili in E costituiscono lo spazio L1(E); sono importanti gli spazi Lp(E) delle funzioni la cui potenza p-esima è sommabile, e in particolare lo spazio L2(E) delle funzioni di quadrato sommabile.

Per serie sommabile ➔ serie.

Nella teoria dei gruppi topologici, una famiglia (xi)i∈I di elementi del gruppo additivo G, con i che varia in un insieme I di indici, si dice famiglia sommabile di s. S se gode della seguente proprietà: fissato un arbitrario intorno U dell’elemento neutro di G, esiste un sottoinsieme finito FU di I tale che per ogni sottoinsieme finito F di I contenente FU, si abbia

^i∈F