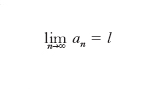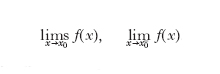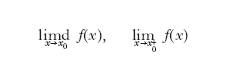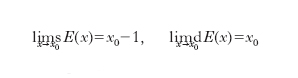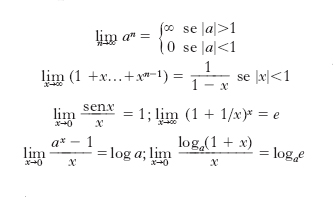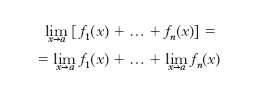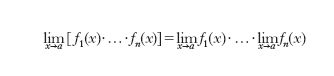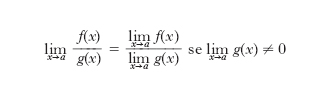limite

Livello massimo, al di sopra o al di sotto del quale si verifica un fenomeno.

Fisica

Angolo limite

In ottica, nel passaggio di un raggio da un mezzo a un altro con indice di rifrazione assoluto inferiore (per es., per la luce visibile, dall’acqua all’aria) l’angolo di incidenza sulla superficie di separazione, superato il quale il raggio non è più trasmesso, essendo riflesso internamente nel primo mezzo (➔ rifrazione).

Geografia

Limite altimetrico

Altitudine oltre la quale cessa un determinato fenomeno fisico, biologico, antropico. Tali l. si dicono topografici quando precisano, di una data regione, il variare effettivo delle altitudini alle quali si verifica il fatto osservato, e medi quando, con interpolazioni arbitrarie, segnano il valore medio tra quelli effettivi.

Limite delle nevi permanenti

Si dice l. climatico la linea altimetrica che separa la zona coperta di neve tutto l’anno, da quella che, almeno in parte, ne rimane priva. Il l. climatico dipende principalmente dalla quantità di precipitazione nevosa, dalla temperatura media dei mesi estivi, ma anche dalle condizioni topografiche o morfologiche; è a più basso livello sui versanti esposti a nord, meno soleggiati e in quelli meno piovosi; la sua altezza assoluta varia in rapporto alla latitudine da 0 m nelle regioni artiche, a 2000-3000 m nelle medie latitudini, a oltre 6000 m nelle regioni tropicali; è variabile, oltreché nello spazio, anche nel tempo.

Si dice invece l. orografico il livello inferiore effettivo al quale arrivano le nevi permanenti, a seconda delle condizioni topografiche; esso è sempre più basso del l. climatico.

Limite della vegetazione

Quota alla quale variano la flora e la vegetazione di una montagna. I piani di vegetazione, in parte corrispondenti alle zone di vegetazione che si distinguono in un continente andando dall’equatore alle regioni polari, sono caratterizzati dalla presenza di certe specie e di certe formazioni che hanno un l. altitudinare inferiore e uno superiore, oltre i quali mancano. Confrontando i due l. di una data specie in territori montani diversi, si osserva che tali l. si abbassano quanto più si procede verso il polo; così molte specie che nelle Alpi non scendono al disotto di 2000 m, nelle regioni artiche crescono al livello del mare; viceversa in Africa, a 3000 m, anziché una flora e vegetazione ipsofila, si trova ancora la foresta temperata. L. del bosco Altezza media alla quale il bosco cessa e iniziano i pascoli. Si può differenziare con difficoltà il l. del bosco a latifoglie in quanto esso sfuma gradatamente in quello ad aghifoglie. Il l. delle foreste a conifere corrisponde abbastanza bene allo sviluppo assoluto dell’altezza delle montagne: sulle Alpi varia da 1700 m, nelle Prealpi Settentrionali, a 2250 m nelle sezioni mediane, a 1950 m nelle Prealpi Meridionali. Il l. è influenzato da molti fattori ecologici e climatici (specialmente dalle precipitazioni).

Geologia

fig. 1A

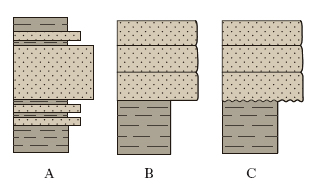
Si definisce l. il contatto tra due unità o corpi geologici, che può essere stratigrafico o tettonico (per faglia o sovrascorrimento). Nelle successioni sedimentarie i l. stratigrafici mostrano differenti caratteri litologici e geometrici e hanno, inoltre, un evidente significato temporale. I l. litologici tra due unità sono sia verticali sia laterali e possono essere graduali (fig. 1A), netti (1B) o erosivi (1C). Nel primo caso la litologia di un’unità viene sostituita gradualmente da quella dell’unità adiacente attraverso sedimenti che hanno caratteri transizionali fra le due. Il l. netto è invece evidenziato da una superficie che pone a contatto due litologie differenti; spesso questo passaggio avviene mediante una superficie di erosione e in tal caso il l. è erosivo.

fig. 2A

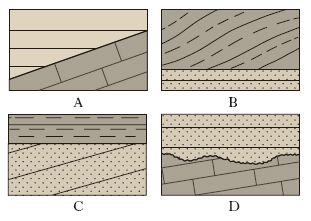
Per quanto riguarda le relazioni geometriche tra due unità stratigrafiche, rispetto alla superficie l. che le separa, esse possono essere concordanti o discordanti. Nel primo caso le due unità mostrano, rispetto al l., strati paralleli tra loro, siano essi orizzontali o inclinati. Due unità sono invece discordanti quando, rispetto al l. che le separa, hanno strati non paralleli tra loro, con diversa angolazione; alcune terminologie, ormai entrate nell’uso comune stratigrafico, per indicare questi tipi di discordanza sono: a) terminazione a onlap (fig. 2A), configurazione in cui gli strati orizzontali di un’unità si appoggiano su una superficie limite inclinata; b) terminazione a downlap (2B), configurazione in cui strati già in origine inclinati si appoggiano su una superficie l. orizzontale o comunque meno inclinata; c) terminazione a toplap (2C), configurazione caratterizzata dall’appoggio di strati orizzontali su una superficie limite anch’essa orizzontale, posta al tetto di strati già in origine inclinati; d) terminazione a troncatura erosiva (2D), caratterizzante il tetto di una unità stratigrafica che sia stata soggetta a erosione, sulla quale si appoggiano successivamente i depositi di una unità più recente. Per quanto riguarda il significato temporale dei l. stratigrafici descritti in precedenza, è evidente che qualora i l. litologici siano graduali, questo indica una continuità di sedimentazione che esprime anche una continuità temporale; viceversa, quando i l. sono netti, essi possono essere indicativi sia di una continuità, sia di una discontinuità nella sedimentazione, che si traduce in una continuità o in una discontinuità temporale; nel caso di l. erosivi, l’evidente discontinuità sedimentaria è sempre indicativa di una discontinuità temporale (lacuna stratigrafica). Ancora con significato temporale, i l. sono diacroni quando hanno differente età geologica lungo tutta la loro estensione, in quanto separano unità stratigrafiche di differente età; sono invece sincroni quando hanno la stessa età geologica per tutta l’estensione che separa le due unità stratigrafiche.

Matematica

Nozione di importanza dominante in quasi tutti i rami della matematica, sorta dall’esigenza di caratterizzare in termini logici rigorosi la tendenza di una variabile numerica ad assumere un determinato valore. L’idea del l. ricorre per la prima volta presso i geometri greci, da Eudosso (metodo di esaustione) a Euclide e Archimede (calcolo di lunghezze, aree, volumi di figure geometriche). Fu poi ripresa e utilizzata sistematicamente da I. Newton e G. Leibniz, ideatori del calcolo infinitesimale, e successivamente sistemata in forma logica precisa nel 19° sec. da B. Bolzano, L.-A. Cauchy e K.T.W. Weierstrass. In seguito la nozione di l. ha assunto un significato via via più ampio e generale.

Limite di una successione

Data una successione a₁, a₂, ..., a_n, ... di numeri reali, si dice che a_n, per n tendente all’infinito, tende al l. determinato e finito l, e si scrive

se, prefissato un ε positivo comunque piccolo, a esso corrisponde un intero p tale che, per ogni n > p, la differenza a_n–l sia in valore assoluto minore di ε. Per es., la successione 1, 1/2, 1/3,..., 1/n,... tende a 0 per n tendente all’infinito. Si dirà invece che a_n tende a +∞ (oppure a −∞) per n→∞ se, prefissato un H positivo comunque grande, esiste in corrispondenza di esso un intero p tale che, per n > p, sia a_n > H (oppure a_n < −H); si scrive in tal caso: lim_n→∞ a_n=+∞ (oppure=−∞). Condizione necessaria e sufficiente affinché la successione a₁, ..., a_n, ... ammetta un l. finito per n → ∞ è che, fissato un ε positivo comunque piccolo, esista in corrispondenza di esso un intero p tale che si abbia | a_m−a_n | < ε, per m, n entrambi maggiori di p (criterio di Cauchy).

Limite di una funzione di una variabile reale

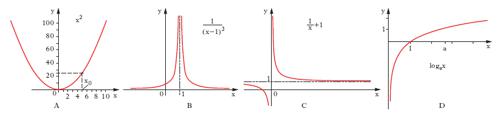
Una successione a₁,..., a_n,... si può considerare come una funzione a(x) di variabile intera: a_n=a(n). Il concetto di l. di una successione si estende allora al caso di una funzione reale di una variabile reale x, suscettibile di assumere i valori di un intervallo dell’asse reale, esclusi, al più, alcuni valori in corrispondenza dei quali la f(x) non è definita. Si dirà allora che la y=f(x), per x tendente a un valore x₀ (che può anche essere uno dei punti nei quali la f(x) non è definita) tende al limite determinato e finito l se, prefissato un ε > 0 comunque piccolo, esiste in corrispondenza un δ > 0 tale che, per ogni valore della x (escluso al più x₀) soddisfacente alla limitazione | x−x₀ | < δ, si abbia: | f(x)−l | <ε. In altri termini, prefissato comunque un ‘intorno’ I di l, esiste in corrispondenza un intorno J di x₀, tale che per ogni x di J accada che f(x) stia in I. In forma intuitiva, si verifica il fatto che quando il valore x si avvicina al valore x₀, il valore f(x) si avvicina quanto si vuole al valore l. Per esprimere in simboli che il l. di f(x), per x tendente a x₀, è uguale a l, si usa una delle scritture: lim_x→x0 f(x)=l; lim_x=x0 f(x)=l; per x → x₀, f(x) → l, o scritture analoghe, che si leggono: limite di f(x), per x tendente a x₀, è uguale a l; oppure: per x tendente a x₀, f(x) tende a l. Sempre in relazione alle funzioni reali di una variabile reale, si definisce la nozione di l. in altri casi fondamentali; si dice che, per x tendente a x₀, il l. di f(x) è uguale a +∞ (in simboli: lim_x→x0 f(x)=+∞) se, per ogni numero H > 0, comunque grande, esiste un δ > 0 tale che, per ogni x≠x0 soddisfacente alla relazione | x−x₀ | < δ, si abbia f(x) > H; con linguaggio intuitivo: quando x si avvicina a x₀, f(x) cresce quanto si vuole; definizione analoga si dà per il limite −∞ e per il limite ∞ (quando cioè | f(x) | tende a +∞). Per quanto riguarda il caso, più strettamente analogo a quello delle successioni, nel quale la variabile indipendente x tenda a +∞ (oppure a −∞), si hanno le due seguenti definizioni (naturalmente si suppone che l’insieme di definizione della funzione considerata sia superiormente, oppure inferiormente, illimitato): si dice che, per x → +∞, f(x) tende a l (e si scrive lim_x→+∞ f(x)=l) se per ogni numero reale positivo ε esiste un numero reale m > 0 tale che per ogni x > m si abbia | f(x)−l | <ε; in forma intuitiva: quando x diventa molto grande, f(x) si avvicina a l quanto si vuole. Si dice che, per x → +∞, f(x) tende a +∞ (e si scrive: lim_x→+∞ f(x)=+∞) se per ogni numero reale positivo H esiste un numero reale m tale che, per ogni x > m, si abbia f(x) > H; in forma intuitiva: quando x diventa molto grande, f(x) diventa grande a piacere. In fig. 3 sono rappresentati, a titolo di esempio, i grafici di quattro funzioni corrispondenti ai quattro casi più importanti sin qui considerati (A, per x tendente a x₀ la funzione f(x)=x² tende a y=f(x₀); B, per x tendente a 1 la funzione f(x)=1/(x−1)² tende a +∞; C, per x tendente a +∞ la funzione f(x)=1/x+1 tende a 1; D, per x tendente a +∞ la funzione f(x)=log_ax tende a +∞). Si noti che, nel primo caso considerato, può non essere definito il valore f(x0) e, anche se esso esiste, non coincide necessariamente con lim_x→x0 f(x). Quindi, se la funzione f(x) è definita per x=x₀ e se lim_x→x0 f(x)=f(x₀)=f(limx_x→x0) si dirà che la funzione è continua in x₀; in tal caso gli operatori ‘limite’ e ‘funzione’ sono, tra loro, permutabili.

Quando, invece di funzioni di punto, si considerino funzioni di insieme (per es., funzioni di linea, di dominio), si può introdurre il concetto di l., purché si assegni in qualche modo una nozione di distanza, nel senso astratto della parola, o una nozione equivalente. Ancora più in generale si introduce, in vari modi, il concetto di l. nella topologia, sia quando si consideri una corrispondenza (o funzione) tra due spazi topologici, sia quando si consideri un insieme variabile in una famiglia di sottoinsiemi dello spazio topologico ambiente===

fig. 3

Specificazioni più frequenti del concetto di limite

Limite destro e limite sinistro

Se, nella definizione di l. per una funzione f(x) data sopra, si prendono in considerazione i soli valori di x maggiori (o rispettivamente minori) di x₀ si dirà che la funzione ammette l. destro (o rispettivamente l. sinistro) in x₀, in quanto si fa tendere x a x₀ dalla destra (o rispettivamente dalla sinistra). Se il l. destro e sinistro esistono e sono entrambi uguali a l, allora l è il l. nel senso ordinario prima definito. I due l. possono però esistere ed essere diversi, dando luogo a un salto, o discontinuità di 1ª specie, come nel caso di una funzione a gradini. Per indicare il l. sinistro di f(x), per x tendente a x₀ si usa solitamente una delle due scritture:

In modo analogo per il l. destro si scrive:

fig. 4

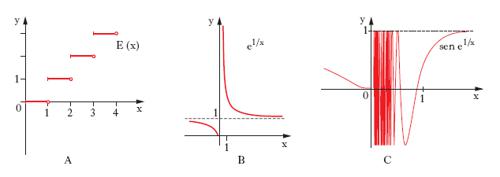
In fig. 4  sono dati alcuni esempi: nel caso A, la funzione parte intera di x, y=E(x) (cioè il massimo numero intero non superiore a x) presenta, per ogni valore intero x ₀, un salto, in quanto:

nel caso B, per la funzione y=e^1/x si ha lims_x→0 y=0, limd_x→0 y=+∞; nel caso C, per la funzione y=sen e^1/x si ha lims_x→0 y=0, mentre non esiste, per x → 0, il l. destro.

Limite diretto o limite inverso 

Le nozioni di l. diretto e di l. inverso si inquadrano nell’algebra omologica (➔ omologia) e costituiscono un’ampia generalizzazione del concetto classico di limite. In primo luogo, infatti, gli elementi dei quali si considera il l. non sono più numeri ma insiemi; di solito, inoltre, questi insiemi sono anche dotati di una medesima struttura algebrica o topologica (per es., possono essere A-moduli oppure spazi topologici). In secondo luogo, mentre nel caso del l. di una successione o di una funzione di variabile reale gli elementi dei quali si considera il l. hanno un ordinamento lineare, nel caso attuale si ha, in una prospettiva molto più generale, solo un ordinamento (➔) parziale o pre-ordine.

Limite per una funzione complessa w(z) di una variabile complessa z

Si dà in maniera sostanzialmente identica ai casi precedenti, salvo a sostituire il valore assoluto con il modulo (enti che del resto si indicano con lo stesso simbolo) e a tener presente che per la variabile complessa esiste un solo modo per tendere all’infinito (➔ intorno).

Limite per una funzione puntuale di punto

Se il punto Q=F(P) variabile nello spazio euclideo E_n è funzione di un punto P, variabile in un insieme A dello spazio

euclideo E_n, si dice che lim_P→P0 F(P)=L (essendo P₀ un punto di accumulazione dell’insieme A), se per ogni numero reale ε > 0 esiste un numero reale δ > 0 tale che per ogni P di A, diverso da P₀ e tale che la distanza P ̅₀ P ̅   sia < δ, si abbia L̅Q ̅< ε.

Limiti fondamentali

Si riportano qui di seguito alcuni l. particolarmente importanti o utili nei calcoli:

Massimo limite e minimo limite 

Quando sia data una variabile ordinata f (➔ variabile), che può essere in particolare una funzione f(P), per la quale si consideri l’ordinamento espresso dalla frase ‘P tende a P₀’, si introducono i concetti di minimo e di massimo l.: data una funzione reale di punto f(P) (o, più in generale, una variabile ordinata), si chiamano minimo e massimo l. della f(P), quando P tende a un punto di accumulazione P₀ (o rispetto al dato ordinamento), le due quantità, eventualmente infinite, e ben determinate, l′, l″, tali che, comunque si fissi un numero reale positivo ε, esista un numero δ che per ogni P per il quale P ̅₀ P ̅  < δ, accada che l′−ε < f(P) < l″+ε; ed esista in ogni intorno di P₀ un punto P₁ per il quale accada che f(P₁) < l′+ε e un punto P₂ per il quale f(P₂) > l″−ε. I numeri trovati si denotano con uno dei seguenti simboli: minlim_P→P0 f(P), maxlim_P→P0 f(P); lim′_P→P0 f(P), lim″_P→P0 f(P); lim f(P), l̅i̅m̅ f(P), o con notazioni analoghe. Se l′=l″=l, la funzione ammette l. uguale a l per P → P₀ (e viceversa); essa si dice regolare in P₀ e precisamente convergente o divergente a seconda che l sia finito o no.

Principio generale della teoria dei limiti

Se la funzione f(u, v,...) è continua nel punto (u₀, v₀,...) e se accade che lim_x→x0 u(x)=u₀, lim_x→x0 v(x)=v₀,…, la funzione F(x)=f(u(x), v(x),...) ammette l. per x → x₀ ed è: lim_x→x0 F(x)=f(u₀, v₀,…). Tale principio serve per ridurre il calcolo del l. di una funzione a quello di l. di funzioni più semplici. Le seguenti formule, di uso continuo in analisi, sono casi particolari del principio:

[1]  formula

[2] formula[3]

Il principio non è direttamente applicabile quando conduce a espressioni del tipo 0/0, 0∙∞, 0^∞, 1^∞, 0⁰, ∞⁰, ∞−∞, dette forme indeterminate. In questi casi, spesso, il l. può essere valutato utilizzando la regola di L’Hôpital (➔ L’Hôpital, Guillaume-François-Antoine de).