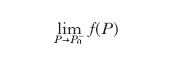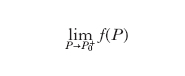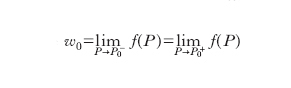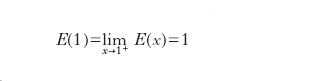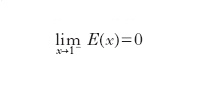discontinuità
Geologia
Superfici di d. sismica Superfici a cui corrisponde un cambiamento repentino (d. di primo ordine) o graduale (d. di secondo ordine) di velocità delle onde sismiche. Esse separano involucri sferici con diversa composizione chimico-mineralogica e diverso stato fisico all’interno della Terra. Le principali d. riscontrate sono: la d. di Mohorovičić (Moho) e la d. di Gutenberg. La Moho, d. di primo ordine, separa la crosta dal mantello ed è posta a profondità variabili tra 30 e 50 km sotto i continenti e 5-15 km sotto gli oceani, anche se non è sempre così netta, soprattutto in aree continentali. La d. di Gutenberg, anch’essa di primo ordine, separa il mantello dal nucleo terrestre ed è posta a profondità di circa 2900 km. Altre d., ma del secondo ordine, sono presenti sia nella crosta, sia nel mantello, sia nel nucleo terrestre.
Matematica
Punto di d. di una funzione è un punto P0 (di accumulazione per l’insieme in cui è definita la funzione) in cui la funzione f(P) non è continua. Ciò può accadere in diversi modi: i due limiti
formula
e formula
esistono, finiti, ma sono diversi tra loro ( d. di prima specie); almeno uno di tali limiti non esiste o è infinito ( d. di seconda specie); i due limiti esistono, sono finiti e uguali tra loro, ma diversi da f(P0) ( d. eliminabile o di terza specie). In quest’ultimo caso la d. può essere rimossa attribuendo a f(P0) il valore
Come esempio di d. eliminabile si consideri la funzione y=x2 per x≠0, y=1 per x=0, rappresentata in fig. 1: è evidente che la d. presente in x=0 può essere rimossa ponendo y(0)=0. Ciò non è possibile, per es., per la funzione y=E(x), nella quale y rappresenta la parte intera del numero reale x, che ha un diagramma a gradini e presenta una d. di prima specie per ogni x intero: in x=1 si ha, per es.,
formula
e formula.
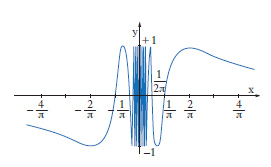
File:IMMAGINI_discontinuita1.jpgIn fig. 2 è rappresentata infine la funzione y=sen (1/x) che presenta un punto di d. di seconda specie per x=0, dove non esiste il limite.
Meteorologia
Presenza di due masse contigue di aria a caratteri differenti, affiancate o sovrapposte; la superficie che le separa viene detta superficie di discontinuità.