armonico
Fisica
In acustica si definiscono suoni armonici o armoniche i suoni componenti, di varia altezza e di frequenza multipla di una stessa, che costituiscono un suono composto insieme con il componente fondamentale.
Analisi a. Ogni funzione periodica f (t) di periodo T, anche non continua, soddisfacente a certe condizioni stabilite da P.G.L. Dirichlet (verificate nei più comuni problemi fisici), si può sviluppare in serie di Fourier, cioè in una serie del tipo
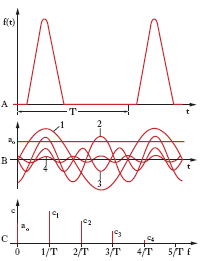
Dal punto di vista fisico ciò significa che ogni fenomeno caratterizzato da una grandezza periodica, anche non sinusoidale, si può sempre considerare come dovuto alla sovrapposizione di infinite oscillazioni semplici, sinusoidali. Lo sviluppo si può in genere ridurre, con ottima approssimazione, a un numero finito, anche piccolo, di termini (fig. 1). L’oscillazione sinusoidale avente il valore del periodo più lungo, uguale a quello T della funzione data, si chiama fondamentale (o prima armonica); le altre, di periodi decrescenti T/2, T/3, T/4, ... (cioè di frequenze crescenti), si dicono armoniche della fondamentale (2ª, 3ª, 4ª ... armonica). Il complesso delle sinusoidi rappresentanti le varie oscillazioni semplici costituisce il cosiddetto spettro della grandezza che descrive il fenomeno. Effettuare l’analisi a. di una grandezza periodica significa determinare i coefficienti dello sviluppo sopra riportato [1]. Tale determinazione può essere fatta per via puramente analitica, secondo la [2], ove sia nota l’espressione analitica della grandezza da analizzare. Più frequentemente si conosce solo l’andamento sperimentale della f (t); per effettuare anche in questo caso l’analisi a. della funzione, sono stati studiati appositi apparecchi detti analizzatori armonici.
L’analisi a. può essere estesa anche a funzioni non periodiche, eseguendone lo sviluppo in integrale di Fourier; ciò equivale a considerare una funzione aperiodica come una funzione periodica con periodo che tende all’infinito.
Matematica
Funzione a. Ogni funzione di due variabili, u (x, y), che soddisfi alla cosiddetta equazione di Laplace.
Analoga definizione vale per le funzioni in tre, o più variabili.
Forma a. Forma differenziale esterna ω, che soddisfa una particolare condizione analitica, generalizzazione dell’equazione di Laplace, del tipo Δω=0, ove Δ=dδ+δd essendo d e δ i simboli, rispettivamente, della derivazione e della coderivazione esterne di una forma differenziale. Le forme a. si presentano pertanto come una generalizzazione molto ampia delle funzioni a.; la grande importanza della loro teoria e delle relative applicazioni risiede non soltanto nella maggiore generalità della condizione cui soddisfano, ma anche nel fatto che esse possono essere definite sopra una varietà differenziabile, mentre le ordinarie funzioni a. sono definite soltanto in uno spazio euclideo.
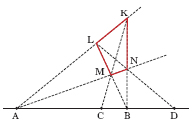
Gruppo a. Un gruppo a. di punti è un gruppo di 4 punti A, B, C, D su una retta tali che il birapporto (ABCD) valga −1. Ciò accade quando e soltanto quando esiste un quadrangolo «completo» LMNK di cui due lati opposti hanno direzioni passanti per A, gli altri due per B, e le diagonali una per C e una per D (fig. 2); esso si dice perciò anche quadrangolo costruttore del gruppo armonico. Operando per proiezioni e sezioni, gruppi a. si mutano in gruppi armonici. I gruppi a. hanno grande importanza nella geometria proiettiva; la definizione si estende a 4 elementi di una qualsiasi forma di 1a specie; quarto a. (dopo A, B, C) è quell’unico punto D tale che (ABCD) = −1.
Proporzione a. Si dice quella formata dai quattro numeri a, b, c, d, nell’ordine indicato, se i loro inversi sono in proporzione aritmetica.
Per la media a. ➔ media; per la progressione a. ➔ progressione.

![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/c/c8/FORMULE_armonico_01.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/73/FORMULE_armonico_02.jpg)