spettro
spettro In varie discipline scientifiche e tecniche, termine frequentemente usato per indicare la composizione armonica di una grandezza variabile nel tempo.
Botanica
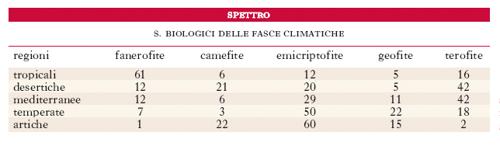
S. biologico Lo s. ottenuto dalle percentuali delle diverse forme biologiche. Originariamente queste forme erano raggruppate in 5 classi (fanerofite, camefite, emicriptofite, geofite, terofite); a queste ne furono aggiunte più tardi diverse altre. Poiché le forme biologiche riflettono le condizioni dell’ambiente, C.C. Raunkaier si valse di queste classi per caratterizzare dal punto di vista fitoecologico le zone climatiche della Terra. Egli calcolò uno s. normale, rappresentante le proporzioni percentuali delle singole forme nel complesso della flora fanerogamica della Terra; con questo s. vengono confrontati gli s. dei diversi territori. Gli s. biologici danno un’idea immediata delle particolarità climatiche di un territorio. Nelle regioni caldo-umide prevalgono le fanerofite, in quelle caldo-aride le terofite; procedendo verso N vanno aumentando le emicriptofite e le camefite; per es., le isole Svalbard hanno il 20% di camefite e solo l’1% di terofite, mentre a Tripoli queste ultime formano il 53% e le camefite il 13% della flora. Nella tabella è riportata la distribuzione percentuale delle categorie biologiche sulla Terra.
S. anabainico Lo s. ottenuto dalle percentuali dei diversi modelli di accrescimento a cui appartengono le specie vegetali presenti in un dato habitat.
S. antesico Lo s. ottenuto dalle percentuali di specie fiorite, nei diversi mesi dell’anno, in un dato territorio. L’andamento è solitamente unimodale, il punto di massimo, denominato picco antesico, corrisponde al mese dell’anno in cui fiorisce il maggior numero di specie.
S. corologico Lo s. ottenuto dalle percentuali dei diversi tipi corologici a cui appartengono le specie vegetali presenti in un dato territorio.
S. pollinico Per un campione geologico di sedimenti, la rappresentazione della frequenza delle varie specie di piante che possono essere desunte dall’analisi pollinica del campione (➔ polline).
Fisica
Insieme delle informazioni riguardanti ogni componente di una radiazione; più specificamente, la distribuzione (comunque visualizzata o registrata) dell’intensità di una radiazione in funzione di una delle grandezze (detta talvolta grandezza spettrale) che la caratterizzano o che caratterizzano le componenti. La grandezza spettrale può essere, per es., la frequenza o la lunghezza d’onda delle componenti sinusoidali di una radiazione elettromagnetica, una coordinata spaziale relativa alla radiazione, l’energia, la quantità di moto o la massa dei corpuscoli che compongono una radiazione corpuscolare ecc.
Il termine è stato originariamente introdotto in ottica per indicare la figura luminosa, a forma di striscia in cui si susseguono i colori dell’iride, che si ottiene raccogliendo su uno schermo bianco la luce emergente da un prisma opportunamente illuminato con luce solare; in seguito è stato usato per indicare la figura cui dà luogo un fascio di luce inviato su un dispositivo disperdente. Estensivamente, è usato per indicare anche l’insieme delle radiazioni elettromagnetiche corrispondenti a un certo intervallo di lunghezze d’onda o di frequenze (s. visibile, s. infrarosso, s. delle microonde, s. dei raggi X).
S. ottici di emissione e di assorbimento
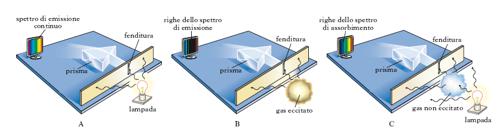
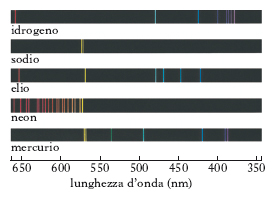
Lo s. della luce emessa da una sorgente (s. di emissione della sorgente o, se questa è una sostanza portata alla luminescenza, s. di emissione della sostanza) può presentarsi, quando lo si raccolga su uno schermo, come una fascia luminosa continua, variamente colorata, o come una fascia luminosa discontinua, a righe o a bande (fig. 1). È uno s. continuo lo spettro della luce solare e continui sono pure, generalmente, gli s. di emissione dei solidi e dei liquidi incandescenti. Uno s. discontinuo, qual è generalmente quello di emissione di un aeriforme, si presenta invece come costituito da un numero più o meno grande di righe sottili, brillanti, di diverso colore (righe spettrali) separate l’una dall’altra da intervalli oscuri, o di zone luminose, apparentemente continue, anch’esse separate a loro volta da intervalli oscuri: i primi si chiamano s. a righe (fig. 2), i secondi s. a bande. Una banda, anche quando venga osservata con strumenti ad alto potere risolutivo, può continuare ad apparire continua: essa si dice in tal caso non risolubile, mentre si dice risolubile se si riescono a osservare, distinte l’una dall’altra, le numerosissime righe dalle quali è costituita. Negli s. a bande, le bande nell’ultravioletto e nel visibile si distinguono, per la loro diversa struttura, dalle bande nell’infrarosso. Le prime sono costituite da un insieme di righe più fitte e intense verso una delle estremità, detta testa della banda, più diradate e meno intense all’estremità opposta, onde si parla di bande sfumate, rispettivamente, verso il rosso o verso il violetto. Le bande risolubili nell’infrarosso sono invece generalmente costituite da un minor numero di righe più uniformemente distribuite, così che non si ha la formazione di una testa.
Oltre che da uno s. d’emissione, ogni sostanza è caratterizzata da uno s. d’assorbimento, costituito dalle righe o bande oscure presenti nello s. di una luce bianca dopo che questa ha attraversato la sostanza in esame (fig. 1). Gli s. di assorbimento dei solidi e dei liquidi sono generalmente costituiti da larghe bande sfumate ai contorni; quelli degli aeriformi invece da righe. Poiché una sostanza è in grado di emettere soltanto le radiazioni che, nelle stesse condizioni, è in grado di assorbire, le righe di assorbimento e le righe di emissione di una medesima sostanza corrispondono alle medesime lunghezze d’onda, o frequenze: è il fenomeno della inversione delle righe spettrali, chiamato così per il fatto che una riga luminosa su fondo oscuro in uno s. di emissione diventa una riga oscura su fondo luminoso nello s. di assorbimento corrispondente. Può peraltro avvenire che i due fenomeni, di emissione e di assorbimento, si sovrappongano, nel senso che una sostanza emetta radiazioni di una determinata frequenza e simultaneamente sia attraversata da luce contenente radiazioni di quella frequenza: se l’intensità della emissione non è tale da compensare l’assorbimento, la riga oscura corrispondente si dice riga invertita.
Per una sorgente, nominalmente monocromatica, e per le radiazioni da essa emesse, la purezza spettrale è una grandezza che in un certo senso misura il maggiore o minore grado di monocromaticità; precisamente, se lo s. della sorgente occupa un certo intervallo Δλ di lunghezze d’onda (definito di volta in volta, con vari criteri) intorno a una lunghezza d’onda λ0, la purezza spettrale relativa a λ0 vale λ0/Δλ.
S. stellari
Gli s. stellari e, in particolare, lo s. solare (➔ Sole) consistono di un fondo continuo di emissione, al quale sono sovrapposte numerose righe e bande oscure di assorbimento (che, nel caso del Sole, prendono il nome di righe o s. di Fraunhofer). Eventualmente, in questi s. si distinguono anche righe o bande di emissione, che provengono da inviluppi gassosi molto caldi della stella (nel caso del Sole, dalla cromosfera e dalla corona). Gli s. stellari permettono di distinguere le stelle in classi spettrali. La classe (o il tipo) spettrale indica ognuna delle categorie (W, O, B, A, F, G, K, C, M, S) in cui sono raggruppati, per somiglianza di caratteristiche, gli s. delle stelle.
Analisi spettrale
L’analisi spettrale consiste nell’identificazione delle righe di uno s. e nella loro interpretazione in relazione alla natura e alle condizioni fisiche della sostanza o del corpo cui lo spettro appartiene.
Nella tecnica, e in particolare in elettronica e nelle comunicazioni elettriche, l’analisi spettrale di un segnale può essere effettuata con appositi strumenti di rivelazione a banda stretta (per es., voltmetri selettivi) accordabili progressivamente sulle varie frequenze nella banda d’interesse. Se il rivelatore utilizzato è di tipo lineare, si ottiene lo s. di ampiezza, se è quadratico lo s. di densità di potenza del segnale. L’analisi spettrale può essere anche effettuata applicando sul segnale la trasformazione di Fourier. Nel caso di segnali campionati ciò è ottenuto mediante l’algoritmo della trasformata veloce di Fourier, o fast Fourier transform (➔ FFT).
Matematica
In matematica il termine s. fu introdotto da D. Hilbert e usato, in un primo tempo, con riferimento agli operatori tra spazi vettoriali. Nel caso che gli spazi siano a dimensione finita, la teoria spettrale è una parte della teoria delle matrici, legata in particolare all’equazione caratteristica, che si sviluppò contemporaneamente allo studio degli operatori risolventi e delle equazioni integrali; vi dettero notevole impulso J.J. Sylvester e G.F. Frobenius. L’unificazione dei due rami di ricerca è merito degli studi di Hilbert e M. Riesz agli inizi del 20° secolo. Una generalizzazione agli spazi lineari-topologici localmente convessi è dovuta a J. Leray (1950).
Nella teoria degli operatori lineari, dato un operatore lineare T di uno spazio di Banach complesso B in sé, si dice s. di T, e si indica con σ(T), l’insieme dei numeri complessi λ tale che non sia invertibile su tutto B la trasformazione λI−T, dove I è l’identità di B in sé. Si dice invece insieme risolvente di T e si indica con ρ(T) l’insieme di tutti i numeri complessi λ tali che esista (λI−T)−1; lo s. è pertanto il complementare del risolvente. Di solito lo studio della struttura di un operatore lineare dipende dal comportamento della trasformazione λI−T. Se lo spazio è B={0}, allora σ(T) è vuoto e quindi il risolvente ρ(T) è l’intero piano complesso. Se B è di dimensione finita, lo s. è un insieme finito. Se T è un operatore lineare limitato, e B≠{0}, lo s. σ(T) è non vuoto, chiuso e limitato. L’estremo superiore dei moduli degli elementi di σ(T) si dice raggio spettrale e si indica con rT; il teorema del raggio spettrale asserisce l’uguaglianza rT=limn→∞ (∥Tn∥)1/n (tale limite è sempre esistente per ogni trasformazione T, e si è indicata con ∥T∥ la norma dell’operatore T). È sempre rT≤∥T∥, e l’uguaglianza è raggiunta quando T è una trasformazione limitata autoaggiunta. Per qualsiasi trasformazione T è σ(Tn)=[σ(T)]n; inoltre lo s. dell’operatore T*, aggiunto di T, coincide con σ(T). Lo s. si suddivide, a seconda delle proprietà di λI−T, in s. puntuale, s. continuo e s. residuo. Un punto del piano complesso appartiene allo s. puntuale se nel dominio di T esiste un elemento x≠0 tale che (λI−T)x=0; λ invece appartiene allo s. continuo se non appartiene allo s. puntuale e se il codominio di λI−T è denso in B, ma non è tutto B; la restante parte dello s. costituisce lo s. residuo. Le funzioni complesse f definite su B, che risultino analitiche su un intorno di σ(T), godono di interessanti proprietà; per es., vale l’uguaglianza f(σ(T))=σ(f(T)) (teorema dell’applicazione spettrale). Se T è un operatore chiuso in uno spazio di Hilbert, l’insieme dei numeri complessi tali che l’immagine λI−T non è chiusa si dice s. essenziale, si indica con σε(T) ed è chiaramente contenuto in σ(T). Questa definizione si estende poi anche agli operatori differenziali definiti in modo puramente formale.