prisma
Poliedro avente per facce due poligoni uguali (basi) posti su piani paralleli e un numero di parallelogrammi (facce laterali) pari al numero dei lati delle basi.
Fisica
In cristallografia, una delle forme semplici che possono presentare i cristalli nei gruppi trimetrico e dimetrico: per es., p. trigonale, p. tetragonale, p. esagonale, a seconda che la sezione sia rispettivamente triangolare, quadrata o esagonale.
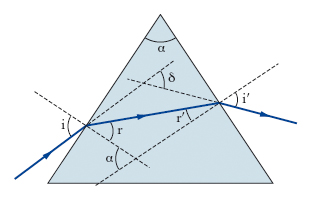
In ottica, il p. ottico, o semplicemente p., è un mezzo omogeneo trasparente limitato da superfici piane non parallele, dette facce del p.; l’angolo diedro α (fig. 1) tra la faccia su cui incidono i raggi e quella da cui i raggi emergono si chiama angolo rifrangente. La forma tipica dei p. ottici è quella a sezione triangolare, ma per particolari esigenze si usano anche p. non triangolari. I p. sono usati in ottica per due scopi principali: il primo, cui adempiono i p. dispersivi, è di provocare, per rifrazione, la dispersione di un fascio di luce opportunamente inviato su una faccia, mentre il secondo, attuato dai p. a riflessione, è quello di provocare, mediante una o più riflessioni totali interne, opportune deviazioni di raggi luminosi. Un raggio di luce, nell’attraversare un p., subisce generalmente una deviazione, a misura della quale si assume l’angolo δ che il raggio incidente forma con il raggio emergente, e al quale si dà appunto il nome di deviazione. Per semplicità, si pensi a un p. triangolare e a un raggio luminoso monocromatico contenuto in un piano normale allo spigolo rifrangente, che incida su una delle facce del p. con un angolo di incidenza i. Se il raggio non subisce nel p. una riflessione totale, si hanno due rifrazioni, una all’ingresso nel p., l’altra all’uscita; indicando con i′ l’angolo di rifrazione nella seconda rifrazione, la deviazione vale: δ=i+i′−α, dove α è l’angolo rifrangente. Se n è l’indice di rifrazione (relativo al mezzo in cui si trova il p., cioè, normalmente, relativo all’aria) del materiale di cui è fatto il p., si ha seni′/senr′=n; a sua volta l’angolo r′ è legato a r dalla relazione r+r′=α mentre l’angolo r è legato a i dalla relazione seni/senr=n; le relazioni ora scritte sono note come formule del p. rifrangente. Se l’angolo rifrangente è piuttosto piccolo (α≤15°) e se piccolo (dell’ordine di qualche grado) è anche l’angolo di incidenza i, le precedenti relazioni si riducono all’unica formula δ≃(n−1)α, con δ indipendente da i. In generale, peraltro, per un determinato p. la deviazione δ varia con continuità al variare dell’angolo di incidenza i, presentando un minimo in corrispondenza a un valore im di tale angolo individuato dall’uguaglianza senim=nsen(α/2). In tali condizioni risulta i=i′=im; r=r′=α/2; il raggio è, nell’interno del p., normale alla bisettrice dell’angolo rifrangente, il raggio incidente e quello emergente sono disposti simmetricamente rispetto al p.; δ assume il valore δm=2im−α. Dalle precedenti formule si ottiene:
Quanto alla possibilità che il raggio penetrato nel p. subisca una riflessione totale sulla seconda faccia rifrangente, ciò come si sa accade se l’angolo di incidenza su questa faccia, r′, è maggiore dell’angolo limite corrispondente alla rifrazione dal p. verso il mezzo circostante, cioè se r′> arcsen(1/n): non è difficile vedere che si ha riflessione totale se α>2arcsen(1/n). Per quanto riguarda le aberrazioni, un p. si presenta come un sistema astigmatico e fortemente cromatico: quest’ultima circostanza, dovuta alla dipendenza della deviazione dall’indice di rifrazione, a sua volta dipendente dalla lunghezza d’onda, è messa a profitto nei p. dispersivi, usati negli spettroscopi, negli spettrografi, nei monocromatori appunto detti a prisma. A misura del potere disperdente di un p. viene assunta la differenza tra le deviazioni minime δm cui il p. in esame dà luogo per radiazioni di lunghezza d’onda pari a 6563 Å (riga rossa C di Fraunhofer) e 4861 Å (riga blu F di Fraunhofer); tale differenza (che raramente giunge a 3°) è detta angolo di dispersione prismatica. I p. a riflessione adempiono a funzioni che potrebbero essere ugualmente assolte da specchi piani opportunamente disposti: la convenienza del loro uso sta nella circostanza che danno luogo a perdite di intensità molto minori.
Matematica
P. indefinito La parte di spazio descritta da un poligono che si muova di moto traslatorio rettilineo, in direzione non parallela al suo piano; in altre parole, considerate più rette parallele r1, r2, …, rn, è la parte di spazio delimitata dalla striscia di lati r1, r2, da quella di lati r2, r3, …, da quella di lati rn, r1. P. finito (o semplicemente p.) La parte di p. indefinito compresa tra due sezioni fatte con piani paralleli; le due sezioni risultano uguali e sono le basi del p., i parallelogrammi intercettati dalle basi sulle facce del p. indefinito sono le facce laterali del p. finito, i loro lati gli spigoli del p. (in particolare gli spigoli laterali sono quelli non appartenenti alle basi). Se le basi sono triangoli, rettangoli, esagoni ecc., il p. si dice triangolare (fig. 2), rettangolare, esagonale ecc.; se le basi sono parallelogrammi si dice anche parallelepipedo. A seconda che gli spigoli laterali siano o no perpendicolari ai piani delle basi, si ha un p. retto oppure un p. obliquo. Un p. retto le cui basi siano poligoni regolari si dice regolare. Il volume di un p. è dato in ogni caso dal prodotto dell’area della base per la distanza delle due basi, detta altezza del p. (h; fig. 2).
Per il p. storto, o antiprisma archimedeo, ➔ poliedro.
Medicina
I p. sono formazioni caratteristiche dello smalto dei denti, detti anche colonne dello smalto; hanno sezione poligonale e sono riuniti insieme da una sostanza cementante.