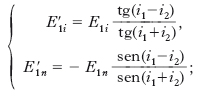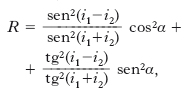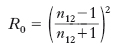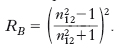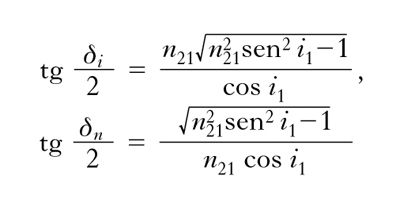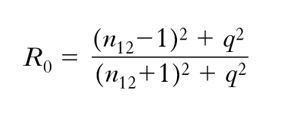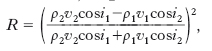riflessione

Filosofia

L’azione di considerare pensando e ripensando con attenzione e scrupolo. Nel linguaggio filosofico, il termine è andato storicamente caratterizzandosi in accezioni più specifiche. In J. Locke la r. designa una delle due fonti della conoscenza (l’altra è la sensazione, che le fornisce il materiale); essa dà origine alle cosiddette idee di r., non ottenibili mediante i sensi (percezione, pensiero, dubbio, credenza ecc.). Per I. Kant la r. è quel particolare stato dello spirito che permette di «scoprire le condizioni soggettive nelle quali possiamo arrivare ai concetti», è «la coscienza della relazione tra le rappresentazioni date e le nostre varie fonti di conoscenza», grazie alla quale può essere colto il loro scambievole rapporto. G.W.F. Hegel, sottolineando il carattere creativo della r. in una prospettiva gnoseologica che rifiuta alcuni dei presupposti fondamentali della posizione kantiana, la vede come attività che caratterizza la libertà del soggetto pensante in quanto non si limita a cogliere una natura delle cose come natura preesistente, ma la produce nel momento stesso in cui la coglie. Di qui la radicale svalutazione di una filosofia della r. in cui l’intelletto umano proceda per astrazione, cioè per separazioni e opposizioni che tiene fisse e insuperabili, rimanendo perciò sostanzialmente legato alla realtà sensibile, incapace di elevarsi al grado della ‘ragione’.

Fisica

In ottica, r. della luce, il fenomeno consistente nel regolare e ordinato rinvio della luce da parte della superficie di separazione di due mezzi dotati di differenti proprietà ottiche. Si chiama riflessività la capacità di una superficie di dar luogo al fenomeno della riflessione.

Per ovvia estensione dal campo delle radiazioni visibili ad altri campi dello spettro elettromagnetico, si parla di r. di onde elettromagnetiche e in particolare, di r. di radioonde ecc. e, passando a onde elastiche, di r. del suono, di r. di onde sismiche (➔ prospezione), di r. delle onde marine (➔ oceanografia) ecc.

L’apparecchio per misurare il coefficiente di r. per onde elettromagnetiche, e in particolare per onde luminose o per radioonde, di superfici materiali è il riflettometro.

Per analogia si parla poi di r. degli elettroni (➔ ottica), di r. di forme d’onda di tensione e di corrente elettrica in una linea (➔ linea) ecc.

R. di radiazioni luminose ed elettromagnetiche in genere

Origine del fenomeno

La r. è un fenomeno che si verifica sistematicamente allorché una radiazione luminosa, ed elettromagnetica in genere, incide sulla superficie di separazione di due mezzi diversi: una parte più o meno grande dell’energia che costituisce la radiazione incidente viene rinviata, propagandosi sotto forma di radiazione riflessa nel mezzo in cui si propaga la radiazione incidente, mentre la restante parte dell’energia raggiante incidente penetra nell’altro mezzo e qui si propaga sotto forma di radiazione rifratta. La diversità dei due mezzi va intesa come diversità delle costanti elettromagnetiche (costante dielettrica, permeabilità magnetica, conduttività elettrica) o, che è lo stesso, come diversità dell’indice di rifrazione assoluto, che sintetizza tali costanti. Se si utilizza la rappresentazione ondulatoria, si ragiona in termini di onde riflesse, incidenti e rifratte. Se si ragiona, nell’ambito dell’ottica geometrica, in termini di raggi di propagazione, si può anche dire che un raggio incidente sulla superficie di separazione di due mezzi diversi dà luogo a un raggio riflesso e a un raggio rifratto (due raggi rifratti se il secondo mezzo è anisotropo: ➔ birifrangenza); la superficie in questione ha il nome di superficie riflettente, o anche di superficie rifrangente quando si vuol sottolineare il fatto che è presente anche una più o meno importante rifrazione.

R. regolare

Quando si parla di r. senza ulteriori qualificazioni ci si riferisce in genere alla r. regolare, o r. speculare, con ciò riferendosi alla circostanza che la superficie riflettente è, almeno nell’ambito della zona d’incidenza, dove cadono i raggi incidenti, una superficie ottica regolare, cioè tale che le eventuali scabrosità e irregolarità siano caratterizzate da dimensioni piccole rispetto alla lunghezza d’onda delle radiazioni incidenti; parlando di r. regolare si sottintende implicitamente anche il fatto che, procedendo in direzione normale alla superficie riflettente, la variazione dell’indice di rifrazione che caratterizza il passaggio da un mezzo all’altro sia piuttosto brusca, e precisamente avvenga in un tratto (che si chiama spessore della superficie riflettente) anch’esso piccolo rispetto alla lunghezza d’onda. Se l’una o l’altra di queste condizioni non sono soddisfatte si ha una r. non regolare, e in particolare una r. diffusa se la superficie è scabra o comunque irregolare, e una rifrazione, con eventuale r. totale, se lo spessore della superficie non è trascurabile nel senso ora precisato.

fig. 1

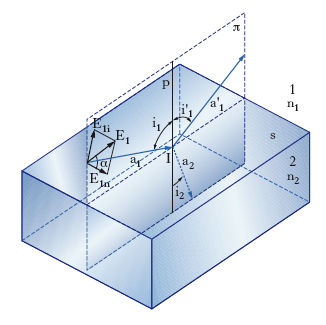
Le leggi della r. regolare, formulate nel linguaggio dell’ottica geometrica, sono: il raggio incidente a₁ (fig. 1), il raggio riflesso a₁′ e la normale p alla superficie riflettente s (per semplicità supposta piana) nel punto I d’incidenza giacciono in un medesimo piano π, detto piano di incidenza (prima legge); l’angolo i₁ d’incidenza (tra a₁ e p) e l’angolo i₁′ di r. (tra p e a₁′) sono uguali (seconda legge). Queste leggi e insieme quelle della rifrazione (relative al raggio rifratto a₂ e all’angolo di rifrazione i₂), possono ottenersi geometricamente a partire dal principio di Fermat o da quello di Huygens (➔ ottica), ovvero con il formalismo dell’ottica ondulatoria, esaminando analiticamente il comportamento delle onde incidenti sulla superficie riflettente; questa seconda via fornisce, oltre alle leggi anzidette, informazioni sull’intensità e sullo stato di polarizzazione delle onde riflesse. Così se si considera, per semplicità, un’onda incidente piana, armonica, polarizzata linearmente, imponendo alle equazioni delle tre onde, incidente, riflessa (propagantesi nel mezzo 1) e rifratta (propagantesi nel mezzo 2), le condizioni ai limiti per i vettori elettrici e magnetici (continuità, nel punto di incidenza I, delle componenti parallele al piano tangente a s in I dei vettori intensità e delle componenti normali a tale piano dei vettori induzione), si trova che, nel caso di mezzi isotropi, il raggio riflesso e rifratto giacciono nel piano definito dal raggio incidente e dalla normale p a s in I, che gli angoli di incidenza i₁ e di r. i₁′ sono uguali, che il rapporto tra il seno dell’angolo di incidenza i₁ e il seno dell’angolo di rifrazione i₂ è costante, e precisamente pari al rapporto (indice di rifrazione relativo del mezzo 2 rispetto al mezzo 1, n₁₂) tra la velocità di propagazione delle onde nel mezzo 1, v₁, e quella, v₂, nel mezzo 2 (➔ rifrazione); si trova inoltre che, indicando con E₁, E₁′, E₂ le intensità del campo elettrico dell’onda incidente (polarizzata linearmente), riflessa e rifratta e con gli indici i, n le componenti rispettivamente parallele e normali di tali vettori rispetto al piano d’incidenza, nel caso di incidenza obliqua (i₁≠0), valgono le relazioni (equazioni di Fresnel della r.):

[1] formula

per incidenza normale (i₁=0°) non si distingue tra le due componenti, e si ha:

[2] formula

Definendo poi come coefficiente (o fattore) di r., o potere riflettente, della superficie s il rapporto R tra l’intensità (proporzionale al quadrato dell’ampiezza del campo elettrico) dell’onda riflessa e l’intensità dell’onda incidente, per tale coefficiente si ha:

[3] formula

essendo α l’angolo tra il piano d’incidenza e il piano di polarizzazione dell’onda incidente.

fig. 2A

R. regolare vetrosa e metallica

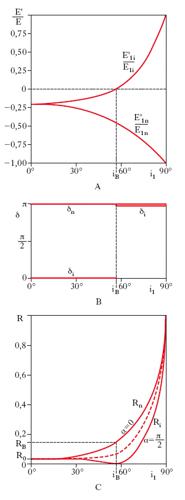
Se i due mezzi sono dielettrici isotropi trasparenti, i loro indici di rifrazione assoluti e l’indice di rifrazione relativo n₁₂ sono grandezze reali (la propagazione avviene senza assorbimento di energia); per di più, se il secondo mezzo è più rifrangente del primo, n₁₂ è una grandezza reale maggiore dell’unità. Dalle [1], [2] si deduce che, passando dall’incidenza normale (i₁=0°), a quella radente (i₁=90°), il rapporto E′_1n/E_1n resta sempre negativo e finito, passando dal valore −(n₁₂−1)/(n₁₂+1) al valore −1 (fig. 2A); cioè un’onda incidente polarizzata nel piano d’incidenza (α=0°) viene sempre riflessa, con inversione di fase all’atto della r. (sfasamento δ_n=180°: fig. 2B). Il rapporto E′_1i/E_1i passa dal valore −(n₁₂−1)/(n₁₂+1) per i₁=0° al valore zero per i₁=i_B=arctgn₁₂ (angolo d’incidenza di Brewster: in queste condizioni risulta i₁+i₂=90°) e poi al valore +1 per i₁=90° (fig. 2A): ciò significa che un’onda incidente polarizzata normalmente al piano d’incidenza (α=90°) viene riflessa con inversione di fase (δ_i=180°) se l’incidenza è compresa tra quella normale e quella brewsteriana e in accordo di fase (δ_i=0°) per incidenza tra quella brewsteriana e quella radente, mentre non viene riflessa se l’incidenza è brewsteriana (fig. 2B). A causa di queste circostanze un’onda comunque linearmente polarizzata, e anche un’onda (per es. luminosa) non polarizzata, subiscono, nella r., una polarizzazione nel piano di incidenza, che è totale se l’incidenza è brewsteriana (➔ polarizzazione). Per quanto riguarda il coefficiente di r., si trova che per incidenza normale esso ha il valore

[4] formula

per incidenza obliqua e onda incidente polarizzata nel piano d’incidenza (α=0°), R passa dal valore R₀ per i₁=0° al valore 1 per i₁=90°, mentre per un’onda polarizzata ortogonalmente al piano d’incidenza (α=90°), R prima diminuisce da R₀ a zero passando dall’incidenza normale a quella brewsteriana, per poi aumentare da zero a 1 quando si passa dall’incidenza brewsteriana a quella radente. Nel caso di un’onda non polarizzata, in corrispondenza all’incidenza brewsteriana il coefficiente di r. assume il valore espresso dalla relazione:

[5] formula

A titolo d’esempio, nella fig. 2C è riportato l’andamento del coefficiente di r. per polarizzazione parallela (R_i), per polarizzazione ortogonale (R_n) al piano d’incidenza e per luce non polarizzata (linea tratteggiata), nel caso della r. della luce su una superficie aria-vetro, con n₁₂=1,5, R₀=0,04, R_B≅0,15 (l’angolo di incidenza i₁ è espresso in gradi sessagesimali; i_B è l’angolo di Brewster, pari a 56°19′). Da questo esempio risulta abbastanza evidente che la r. alla superficie di mezzi trasparenti (la r. vetrosa) è scarsamente efficiente, salvo che per grandi angoli di incidenza. Fa eccezione il caso in cui, contrariamente a quanto prima ammesso, il secondo mezzo sia meno rifrangente del primo (per es., passaggio dal vetro all’aria). In queste condizioni, n₁₂ è minore dell’unità; le variazioni di fase che hanno luogo sono esattamente le inverse di quelle viste in precedenza per angoli di incidenza minori dell’angolo limite i_l=arcsenn₁₂; per i₁>i_l le [1] forniscono per gli sfasamenti δ_i, δ_n relativi alle componenti E′_1i, E′_1n i valori:

fig. 3A

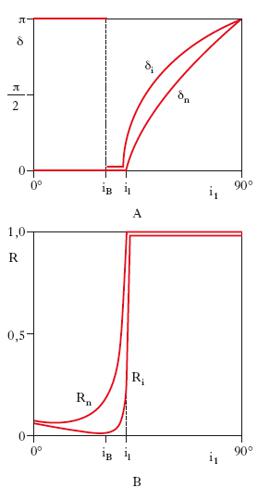
In fig. 3A sono mostrati gli andamenti di δ_i e δ_n per n₂₁=1,51. Per quanto riguarda il coefficiente di r., è facile vedere che valgono le relazioni precedenti per i₁<i_l, mentre per incidenza uguale o maggiore di quella limite, R assume il valore massimo, cioè 1, corrispondentemente al fatto che tutta l’energia incidente viene riflessa: è il fenomeno della r. totale (fig. 3B).

Se il mezzo su cui incidono le onde è un dielettrico con perdite o un mezzo elettricamente conduttore, cioè un mezzo assorbente, l’indice di rifrazione risulta una grandezza complessa, la cui parte reale, n₁₂, è l’indice di rifrazione inteso nel senso ottico ordinario e la cui parte immaginaria, q, dà conto dell’assorbimento di energia. Valgono ancora formalmente le [1]÷[3], a patto di tener presente che, a norma della seconda legge della rifrazione, l’angolo di rifrazione i₂ è complesso. In generale anche il coefficiente di r. risulta complesso; una radiazione incidente polarizzata linearmente dà luogo a una radiazione riflessa polarizzata ellitticamente. In particolare per incidenza normale il coefficiente di r. vale:

[6] formula.

fig. 4

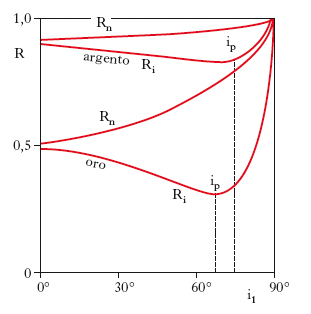
Se il mezzo riflettente è relativamente poco conduttore, per modo che q≪n₁₂, le correzioni da apportare alle formule date prima per il caso della r. vetrosa sono piuttosto modeste e in genere lecitamente trascurabili; così la [6] si riduce, con buona approssimazione, alla [4]. Nel caso di un buon conduttore, qual è, tipicamente, un metallo, la fenomenologia, nota come r. metallica, è più complessa, essendo determinata dal comportamento dei portatori di carica (per un metallo, elettroni di conduzione) sotto l’azione del campo elettrico delle onde incidenti. Si può dire che per lunghezze d’onda relativamente grandi (all’incirca maggiori di 10 μm) il coefficiente di r. è piuttosto grande e non fortemente dipendente dalla frequenza delle onde (per λ>30 μm è praticamente uguale a 1). Per onde di lunghezza minore intervengono fenomeni di rilassamento e di risonanza, per cui la r. perde di efficienza e assume un carattere fortemente selettivo rispetto alla frequenza; ciò spiega, per es., la caratteristica colorazione che assumono le superfici metalliche illuminate da luce bianca. Il coefficiente di r. metallica è comunque sempre piuttosto alto e molto maggiore del coefficiente di r. vetrosa (eccezion fatta per il caso della r. totale): per il vetro R₀ è nel campo ottico dell’ordine di 0,04 mentre per l’alluminio è dell’ordine di 0,85. Per tale motivo i riflettori, cioè gli specchi, sono di norma metallici (alluminio, argento, platino ecc., in forma di lamine o, più spesso, come pellicole depositate su lamine di vetro). Va osservato che per incidenza obliqua, a differenza di quanto accade per i dielettrici, non esiste un angolo di Brewster (fig. 4): un’onda incidente polarizzata linearmente viene sempre riflessa, qualunque sia il piano di polarizzazione e l’angolo d’incidenza. In generale l’onda riflessa è, come accennato, polarizzata ellitticamente, salvo i casi dell’incidenza normale (i₁=0°) e dell’incidenza radente (i₁=90°), nei quali si conserva la polarizzazione lineare.

R. diffusa

È il fenomeno, detto anche diffusione per r. o diffusione superficiale, che si ha quando onde incidono su una superficie che non abbia i requisiti di regolarità occorrenti per la r. speculare, e cioè abbia irregolarità o disomogeneità di dimensioni confrontabili con la lunghezza d’onda della radiazione incidente; quest’ultima viene allora rinviata in modo disordinato in varie direzioni. Può accadere che il rinvio delle onde incidenti avvenga pressoché uniformemente in tutte le direzioni, in modo praticamente indipendente dall’angolo d’incidenza: si parla allora di r. diffusa uniforme. Una superficie che dia luogo a una r. del genere appare uniformemente illuminata da qualunque direzione la si guardi (l’intensità della radiazione diffusa obbedisce alla legge di Lambert, e cioè, nel caso di una superficie diffondente piana illuminata normalmente, è proporzionale al coseno dell’angolo che la direzione d’osservazione forma con la normale alla superficie).

R. interna

È il complesso delle r. che la luce subisce sulle superfici rifrangenti costituenti un sistema diottrico, cioè sulle superfici di lenti, prismi, lamine ottiche ecc. Tali r. risultano dannose, sia perché portano a una perdita di luce, sia perché la luce riflessa può dar luogo a immagini spurie, aloni ecc. Questi dannosi effetti vengono contrastati, sia riducendo l’entità delle r., mediante trattamento antiriflettente delle superfici in questione, sia ricoprendo di vernici nere opache la parte interna dei supporti dei dispositivi ottici, in modo da assorbire la luce riflessa.

La locuzione r. interna è talora usata anche per indicare la r. totale.

R. multipla

È quella che si verifica quando una radiazione elettromagnetica incide successivamente su più superfici riflettenti.

R. del suono e di onde elastiche in genere

Considerazioni analoghe a quelle svolte per i fenomeni di r. di onde elettromagnetiche possono essere fatte a proposito della r., regolare oppure diffusa, che subiscono onde elastiche, e in particolare sonore, incidenti su una superficie che separi due mezzi caratterizzati da costanti elastiche diverse o, che è lo stesso, da una diversa velocità di propagazione per le onde; vi è solo da tener presente, per quanto concerne la polarizzazione, che mentre nel caso elettromagnetico si ha a che fare con onde trasversali, nel caso elastico le onde possono essere sia longitudinali sia trasversali. Ragionando in termini geometrici, per raggi, la formulazione delle leggi della r. regolare è identica a quella della r. di onde elettromagnetiche; salvo un diverso formalismo, sostanzialmente identica è anche la trattazione analitica, a partire dalle equazioni delle onde incidente e riflessa: le condizioni da imporre sulla superficie riflettente riguardano la continuità della componente secondo tale superficie della velocità delle particelle e la continuità della pressione. Il coefficiente di r. regolare, rapporto tra l’intensità dell’onda riflessa e quella dell’onda incidente risulta, per un’onda incidente armonica, longitudinale:

essendo ρ₁, ρ₂ le densità e v₁, v₂ le velocità di propagazione nei due mezzi, i₁ l’angolo di incidenza, i₂, l’angolo di rifrazione. La considerazione di fenomeni di r. regolare, totale e diffusa subiti da onde elastiche ha particolare rilevanza in sismologia, per le onde sismiche e, in acustica architettonica, per quanto riguarda i suoni.