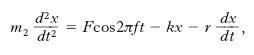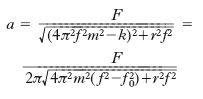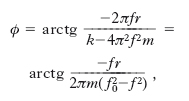risonanza

Fenomeno per cui l’ampiezza delle oscillazioni indotte in un sistema oscillante (meccanico o elettrico) tende, in particolari condizioni, a esaltarsi. Per analogia, ogni fenomeno in cui una grandezza assume valori singolari, e in particolare valori singolarmente grandi, in corrispondenza a determinati valori di una grandezza da cui dipende.

Astronomia

Si dice che due pianeti (o due satelliti) si trovano in uno stato di r., quando il periodo di rivoluzione di uno di essi è una frazione del periodo dell’altro (per es., 1/4, 1/3, 1/2, 2/3 ecc.). Quando ciò si verifica, i due oggetti riassumono periodicamente le stesse posizioni reciproche, sicché le perturbazioni che il corpo più massiccio produce, con il suo campo gravitazionale, sul moto dell’altro si sommano con effetti progressivamente maggiori.

Chimica

Nella teoria del legame di valenza, la configurazione elettronica di una molecola viene descritta da più strutture, ognuna delle quali è detta forma limite o mesomera o canonica fra le quali la struttura molecolare ‘risuona’. Ogni forma limite si ottiene dall’altra ridistribuendo, in modo appropriato, le coppie di elettroni di valenza tra gli atomi legati.

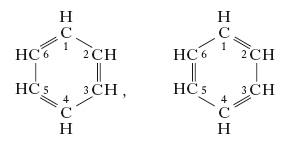
Un esempio classico di applicazione del concetto di r. a una molecola è quello del benzene, le cui forme limite più importanti sono le cosiddette formule di Kekule (➔ Kekule von Stradonitz, Friedrich August):

Si ammette che la struttura del benzene ‘risuoni’ tra tali forme limite; in altre parole, le 3 coppie di elettroni dei legami π non rimangono confinate tra 2 atomi di carbonio adiacenti ma sono condivise da tutti i 6 atomi di carbonio dell’anello.

Fisica

Definizione e applicazioni

Il fenomeno della r. può manifestarsi se un sistema oscillante (meccanico o elettrico) è sottoposto all’azione di una sollecitazione armonica; le oscillazioni forzate del sistema hanno la stessa frequenza f della sollecitazione, e ampiezza e fase iniziale che dipendono da f; la r., o propriamente la r. d’ampiezza, consiste nel fatto che quando f assume un valore all’incirca coincidente con la frequenza propria di oscillazione del sistema (o con una delle frequenze proprie, se il sistema ne ha più di una), l’ampiezza assume un valore massimo. Accanto a questa, si considera anche una r. d’energia, che avviene a una frequenza poco diversa dalla precedente e che consiste nel massimizzarsi dell’energia in gioco nel sistema, cioè dell’interazione energetica fra il generatore della sollecitazione e il sistema oscillante. Si consideri, per es., il semplice sistema oscillante meccanico costituito da un punto materiale P, di massa m, sollecitato a spostarsi lungo una direzione l da una forza variabile sinusoidalmente nel tempo t, Fcos(2πft), e soggetto anche a una forza di richiamo elastica e a una forza resistente, proporzionale alla velocità; fissato su l un sistema di ascisse x, il moto del punto viene a essere descritto dall’equazione:

essendo k, r opportune costanti, non negative. Il moto a regime, cioè dopo che si sia esaurito il transitorio iniziale, risulta essere armonico, x=acos(2πft−ϕ), con ampiezza

e sfasamento rispetto alla forza vibromotrice

fig. 1

essendo f₀=(k/m)^1/2/(2π) la frequenza propria delle oscillazioni libere di P in assenza di forza resistente (➔ oscillatore); quanto all’energia cinetica di P, per il suo valor medio si ha: E_m=π²mf²a². Come si vede, ampiezza a, energia E_m e fase iniziale ϕ dipendono, fermi restando la massa m e il coefficiente k della forza di richiamo, dalla frequenza f della sollecitazione e dal coefficiente r della forza resistente; gli andamenti di a, E_m, ϕ al variare del rapporto f/f₀ e per vari valori della quantità b=r²/(4mk) sono riportati nella fig. 1. E_m è massima, cioè si ha r. d’energia, quando f=f₀, qualunque sia b, cioè qualunque sia l’entità della forza resistente (beninteso entro i limiti in cui esista un regime di oscillazioni forzate per P); l’ampiezza a è massima, pari a F/[2πf₀r(1−2b)^1/2], cioè si ha r. d’ampiezza, quando f=f₀(1−2b)^1/2 e purché b non sia troppo grande: in effetti, per b≥0,5 non esiste più una r. d’ampiezza, come si deduce dalla formula ora data e come mostra la fig. 1A. In molti casi pratici i sistemi oscillanti sono caratterizzati da una forza resistente piuttosto piccola (r²≪4mk), per cui la quantità b è relativamente piccola e trascurabile rispetto alle altre grandezze in gioco; in questi casi, la r. d’ampiezza avviene sensibilmente alla stessa frequenza della r. d’energia, cioè alla frequenza propria f₀: di qui l’uso, comodo ancorché non rigoroso, di non distinguere in pratica le due r. e le relative frequenze. Per f=f₀ si ha comunque ϕ=−π/2 rad e a=F/(2πf₀r)=F/[r(k/m)^1/2]; nel caso teorico di forza resistente nulla (r=0), l’ampiezza sarebbe infinitamente grande. Una caratteristica piuttosto importante è l’acutezza di r., che, come il termine stesso lascia intendere, è in relazione con la forma della curva di r., cioè dell’andamento dell’ampiezza o dell’energia delle oscillazioni del sistema in funzione della frequenza, e che esprime la maggiore o minore rapidità con cui l’ampiezza cresce e descresce al variare della frequenza intorno alla frequenza di r.: un sistema che abbia una r. piuttosto acuta (per es., come quella descritta dalla curva d’ampiezza in fig. 1A per b=0,01) costituisce un buon risonatore.

fig. 2

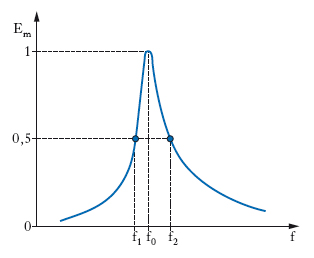
L’acutezza di r. può essere quantificata in vari modi. Un modo abbastanza usuale è di fare riferimento all’estensione dell’intervallo di frequenze delimitato dalle due frequenze f₁, f₂ alle quali l’energia associata alle oscillazioni del sistema si riduce a metà di quella che si ha alla r. (fig. 2): si ha f₂−f₁=r/(2πm). È utile al riguardo introdurre il cosiddetto fattore di qualità (o di merito) per la r. del sistema, pari, per un sistema caratterizzato da valori piuttosto piccoli di b, cioè, come si usa dire, per un sistema poco smorzato, al rapporto Q=f₀/(f₂−f₁) e quindi pari a 2πf₀m/r=(km)^1/2/r: quanto minore è r, tanto maggiore è Q e tanto più stretto è l’intervallo f₂−f₁. Il fattore di merito risulta anche pari al rapporto fra l’ampiezza alla r. e l’ampiezza limite a₀ (fig. 1A) che si avrebbe per f=0 (sollecitazione statica), di modo che esso indica anche quante volte l’ampiezza alla r. è maggiore di quella che si avrebbe in condizioni statiche: di qui l’uso di chiamare Q anche coefficiente di amplificazione per r. o, semplicemente, coefficiente di risonanza.

fig. 3 A

Le considerazioni precedenti si estendono senza difficoltà dal caso del punto materiale al caso di un sistema oscillante meccanico qualunque, e in particolare acustico; per questi sistemi complessi è spesso utile, sia dal punto di vista qualitativo sia dal punto di vista della trattazione analitica, il ricorso all’analogia elettromeccanica (➔ elettromeccanica, analogia), cioè il riferimento analogico ai fenomeni di r. che avvengono in circuiti elettrici: in questi, in opportune condizioni, la carica o l’intensità della corrente fatta circolare da un generatore di forza elettromotrice periodica assumono un valore massimo. Per la cosiddetta r. elettrica serie, cioè per la r. in circuiti con elementi lineari normali in serie (fig. 3 A), la situazione è descritta dall’equazione

analoga a quella del punto materiale oscillante: q è la carica elettrica che scorre nel circuito, Fcos(2πft) è la forza elettromotrice impressa, mentre L, C, R sono, rispettivamente, induttanza, capacità, resistenza del circuito. Valgono i risultati precedentemente indicati, a patto di sostituire a con q, m con L, r con R, k con 1/C. Così, la frequenza propria in assenza di resistenza (R=0), che è la frequenza di r. dell’energia, vale f₀=(2π)⁻¹(LC)^−1/2, mentre la frequenza di r. della carica, nel caso usuale di un circuito poco smorzato (R²≪4L/C), vale f₀[1−(R²C)/(2L)]^1/2; la carica vale FL{2C/[R²(2L−R²C)]}^1/2 alla r. d’energia e F(LC)^1/2/R, che è il valore massimo, alla r. di carica; lo sfasamento fra carica e forza elettromotrice vale −π/2 alla r. d’energia e arctg(−{[4L/(R²C)]−2}^1/2) alla r. di carica; il fattore di qualità vale Q=2πf₀L/R= (2πf₀CR)⁻¹=(L/C)^1/2/R; alla r. d’energia (f=f₀) la reattanza induttiva, 2πfL, e quella capacitiva, (−2πfC)⁻¹, si equivalgono, e quindi l’impedenza si riduce alla sola resistenza: alla r. d’energia s’accompagna quindi un minimo dell’impedenza, cioè una r. d’ammettenza. Nella maggior parte delle applicazioni ci si riferisce peraltro all’andamento dell’intensità di corrente nel circuito, i=dq/dt, più che all’andamento della carica q. Per quanto riguarda dunque la r. di corrente, si trova che questa avviene al massimo di ammettenza, cioè alla frequenza f₀, alla quale l’intensità assume il valore massimo F/R (fig. 3B) e lo sfasamento fra intensità e forza elettromotrice diviene nullo (fig. 3C): in queste condizioni il circuito si comporta come se fosse puramente resistivo (fuori della r., invece, il circuito, come risulta dalla fig. 3C, si comporta induttivamente per f<f₀, capacitivamente per f>f₀). Al variare della frequenza, vi è anche una r. per la tensione ai capi della capacità, che si ha quando f assume il valore di r. per la carica, e per la tensione ai capi dell’induttanza, che si ha per la frequenza f₀[1+(R²C)/(2L)]^1/2, leggermente maggiore sia della frequenza di r. di carica sia di quella di r. di corrente. Va osservato che il circuito può essere portato in r. con una forza elettromotrice impressa di data frequenza f fissa, variando la sua frequenza propria f₀ modificando il valore di L o di C (messa in r. o sintonizzazione del circuito). Per circuiti poco o pochissimo smorzati (al limite, per R=0), le frequenze di r. delle tensioni capacitiva e induttiva coincidono fra loro e con la frequenza propria f₀. Le tensioni ai capi della capacità e dell’induttanza sono alla r. di corrente di uguale ampiezza e controfase, di modo che si bilanciano esattamente, e il fattore di qualità viene a rappresentare il rapporto fra la tensione ai capi dell’induttanza e la forza elettromotrice impressa: Q risulta quindi indicativo non soltanto dell’acutezza di r., ma anche dell’amplificazione di tensione conseguente alla r., grandezza di primario interesse, per es., per amplificatori selettivi facenti uso di circuiti oscillanti.

fig. 4A

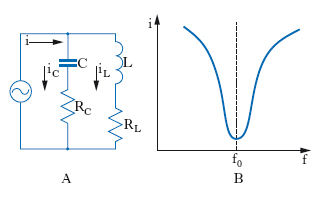
Per la r. in parallelo, cioè per quella che avviene in circuiti con elementi in parallelo fra loro (fig. 4A), si possono svolgere considerazioni analoghe alle precedenti, tenendo conto della dualità delle disposizioni circuitali: grandezze dualmente corrispondentisi sono intensità di corrente e tensione, impedenza e ammettenza, resistenza e conduttanza ecc. Ci limiteremo a sottolineare la circostanza che si ha ora una r. d’impedenza, cioè si ha un massimo di quest’ultima grandezza, e quindi un minimo d’intensità di corrente; ciò accade alla frequenza f′ definita dalla relazione 2πf′={(R_L²C−L)/[LC(R_C²C−L)]}^1/2, dove i simboli adottati hanno il significato illustrato nella fig. 4A; se gli elementi resistivi R_L, R_C, sono trascurabili, tale frequenza viene a coincidere con la frequenza propria f₀ del circuito. Essendo massima l’impedenza, alla r. risulta minima l’intensità della corrente erogata dal generatore di forza elettromotrice (fig. 4B): per tale motivo si dice che si ha antirisonanza (di corrente) e il circuito così eccitato è chiamato circuito antirisonante. Alla r., pur essendo minima la corrente i erogata dal generatore, è massima la corrente che scorre sia nell’induttanza (i_L) sia nella capacità (i_C), ed è quindi massima la tensione ai capi di ognuno dei due elementi reattivi, per i quali si ha dunque una r. di tensione. Va osservato che i circuiti schematizzati nelle fig. 3  e 4 sono circuiti equivalenti a circuiti reali a costanti sia concentrate sia distribuite, salvo, in quest’ultimo caso, a definire opportunamente la frequenza propria o le frequenze proprie.

I fenomeni di r. sono in qualche caso dannosi, e si cerca quindi di evitarli, in qualche altro caso utili. Per es., sono dannosi, e in qualche caso fortemente pericolosi, fenomeni di r. che si destino in strutture sollecitate da forze di intensità variabile nel tempo; la notevole ampiezza delle oscillazioni alla r. può danneggiare la struttura o quanto meno renderne difficile il normale uso, e per evitare ciò si pone la massima attenzione a che eventuali frequenze proprie di oscillazione della struttura abbiano valore nettamente diverso dalle frequenze caratteristiche della sollecitazione; meglio ancora, quando è possibile si dota la struttura di dispositivi dissipatori dell’energia (per es. ammortizzatori) in modo da portarsi nelle condizioni sopra indicate (b>0,5) per evitare l’insorgere di oscillazioni di risonanza. Sempre restando nel campo meccanico, sono invece spesso utili in acustica fenomeni di r.: basta pensare all’esteso uso che si fa di sistemi risonanti (risonatori acustici, casse di r.) negli strumenti musicali e nella tecnica musicale in genere. Molto estesa è poi l’utilizzazione di fenomeni di r. elettrica in elettronica e in particolare in radiotecnica, in cui i già ricordati amplificatori a circuiti oscillanti sintonizzati, vari tipi di filtri elettrici, gli invertitori a r. e molti tipi di antenne costituiscono notevoli esempi di importanti applicazioni.

Particolari fenomeni di risonanza

R. di ciclotrone

Una particella in moto, di massa m e carica q, descrive in un campo magnetico trasversale uniforme, d’induzione B, una circonferenza, con velocità angolare qB/m e frequenza (frequenza di ciclotrone) ν_c=qB/(2πm); tale particella può interagire con un campo elettromagnetico, assorbendo energia raggiante di frequenza pari a quella di ciclotrone: a tale interazione energetica selettiva si dà il nome di r. di ciclotrone.

R. geometrica

Fenomeno di r. tra le caratteristiche geometriche del moto degli elettroni liberi in un cristallo sottoposto a un campo magnetico H e la lunghezza d’onda λ di un campo ultrasonoro propagantesi ortogonalmente a H: è possibile cessione di energia dal campo ultrasonoro agli elettroni soltanto quando il diametro delle traiettorie circolari di questi risulta essere un multiplo intero di λ. Tale fenomeno di r. introduce nell’attenuazione ultrasonora presentata dal cristallo una periodicità con periodo inversamente proporzionale al prodotto λH.

R. magnetica nucleare

Fenomeno di r. nell’interazione fra un campo a radiofrequenza e momenti magnetici nucleari; anche, metodo di spettroscopia a radiofrequenza basato su tale fenomeno; generalmente è indicata con la sigla RMN o anche NMR (nuclear magnetic resonance). I nuclei atomici, in quanto dotati di momento magnetico proprio, interagiscono con un campo magnetico esterno tendendo a disporsi in una delle posizioni consentite rispetto alla direzione del campo medesimo (paramagnetismo nucleare); precisamente, se l’asse z è parallelo al campo, la componente di un momento magnetico nucleare secondo quest’asse può assumere uno dei valori m_z=γμ_nM_I, essendo γ il rapporto giromagnetico nucleare, μ_n il cosiddetto magnetone nucleare, M_I il numero quantico magnetico (cioè la componente dello spin nucleare nella direzione del campo, in unità ℏ) che può assumere i (2I+1) valori I, I−1, ..., −(I−1), −I, con I numero quantico di spin nucleare; in corrispondenza al fatto che γ può essere maggiore oppure minore di zero, il momento magnetico può essere parallelo e concorde oppure parallelo e discorde con lo spin. Alle (2I+1) posizioni, definite dalla relazione precedente, che il nucleo può assumere nel campo corrispondono energie E diverse: E=−γμ_nM_IH₀, essendo H₀ l’intensità del campo; a transizioni fra questi livelli energetici corrisponde l’assorbimento o l’emissione di fotoni la cui frequenza, tenendo conto del fatto che sono consentite soltanto le transizioni per le quali M_I vari di ±1, può avere i valori: ν₀=γμ_nH₀/h, con h costante di Planck. Risulta dunque che se sul sistema atomico in esame agisce, oltre un campo magnetostatico, d’intensità H₀, un campo elettromagnetico la cui frequenza abbia il valore ν₀ ora ricordato, si ha, e in ciò consiste la r., un assorbimento di energia da parte del nucleo, che muta il suo orientamento spaziale rispetto al campo statico: per es., per H₀≅10⁶ A/m il protone ha una frequenza di r. magnetica nucleare di circa 536 MHz. Così, se si mantiene costante H₀ facendo variare la frequenza ν del campo elettromagnetico e in qualche modo si valuta l’assorbimento di energia elettromagnetica, si riesce a misurare la frequenza ν₀ e da questa, mediante le relazioni precedenti, si può misurare il momento magnetico dei nuclei interessati; si può anche far variare l’intensità H₀ del campo statico anziché ν.

La prima osservazione del fenomeno della RMN fu eseguita da I.I. Rabi e collaboratori nel 1939 su atomi liberi (fascio di atomi); i primi esperimenti nella materia condensata furono condotti nel 1946 dai gruppi di F. Bloch e di E.M. Purcell.

In campo biomedico, la r. magnetica nucleare rappresenta un metodo per l’analisi di complessi molecolari, basato sull’esame dei loro spettri di assorbimento delle radioonde per r. magnetica nucleare, e applicato a cellule o frammenti di tessuto o organi in perfusione. Essa trova due settori di applicazione: la tomografia RMN e la spettroscopia RMN in vivo. La prima consente di ottenere immagini bi- e tridimensionali di sezioni del corpo. Rispetto ad altre metodiche, presenta numerosi vantaggi: l’assenza di artefatti dovuti alle strutture ossee, la possibilità di ottenere sezioni a vario orientamento (sagittale, trasversale ecc.), invasività quasi nulla e impiego di radiazioni non ionizzanti. Non necessita di mezzi di contrasto, pur potendosi ottenere immagini a elevato contrasto e potere risolutivo. Numerose sono le condizioni patologiche che possono essere diagnosticate attraverso l’impiego della tomografia RMN: a livello cranico, della colonna e del midollo spinale (malformazioni, processi morbosi di natura vascolare, tumorale, traumatica ecc.); a livello del mediastino, del fegato, del pancreas, dei reni e dei surreni, della pelvi, dell’apparato muscoloscheletrico. A livello del tronco, grazie a particolari accorgimenti tecnici, si è resa possibile la sincronizzazione con i movimenti respiratori e cardiaci. Per l’apparato cardiovascolare, grazie alla tomografia RMN, è possibile effettuare sia valutazioni morfologiche sia misure di flusso ematico. La spettroscopia RMN in vivo consente di valutare, senza necessità di effettuare prelievi bioptici, la funzionalità metabolica e fisiologica di organi e tessuti (muscoli, cellule epatiche, tumorali, linfoidi ecc.). Inoltre, sembra poter offrire nuove potenzialità, soprattutto in ambito oncologico, la scoperta di sostanze con affinità elettiva per talune forme patologiche (per es., tumori). Tali sostanze, marcate con gruppi paramagnetici, metterebbero in risalto nella tomografia RMN la parte patologica, fino a dimensioni dell’ordine del millimetro. Inoltre, data la loro specificità, determinerebbero in maniera univoca di quale patologia si tratti, consentendo una diagnosi e di conseguenza una terapia precoci ed efficaci.

R. paramagnetica elettronica o di spin elettronico

Fenomeno di accoppiamento risonante tra il momento magnetico elettronico, in un campo magnetico statico, e un campo a radiofrequenza; anche, tecnica d’osservazione che fa uso di tale fenomeno. Generalmente è indicata con la sigla RPE. Il meccanismo di accoppiamento è identico a quello della r. magnetica nucleare e ha luogo in quelle sostanze in cui si abbiano elettroni disaccoppiati; la regione interessata è quella delle microonde. La r. di spin elettronico fornisce informazioni non soltanto sulla presenza e sul numero di tali elettroni, ottenibili anche da misure di paramagnetismo elettronico, ma anche sulla distribuzione degli elettroni nella molecola. Tale tecnica è particolarmente usata nello studio degli orbitali liberi degli elementi di transizione, dei legami non saturati nei radicali liberi, degli elettroni di conduzione nei metalli, dei donatori e accettori nei semiconduttori, dei difetti indotti da radiazione.

In biochimica, la spettroscopia di r. paramagnetica elettronica è utilizzata come tecnica analitica per lo studio dei meccanismi catalitici dei metalloenzimi, dei meccanismi molecolari delle reazioni radicaliche e delle reazioni di ossidoriduzione che comportano l’intervento dell’ossigeno molecolare (siano esse enzimatiche o non enzimatiche), per determinare la presenza di sostanze radicaliche prodotte nelle cellule a seguito di stress ossidativi (radicale ascorbile derivante dall’acido ascorbico; ione superossido, radicale ossidrile e ossigeno singoletto derivanti dall’ossigeno molecolare) ecc.

R. in processi nucleari

In fisica nucleare si parla di r. per indicare che la sezione d’urto di un processo di diffusione (scattering) o di una reazione nucleare presenta dei massimi pronunciati in corrispondenza di certi valori dell’energia della particella incidente; nelle curve rappresentanti l’andamento, in funzione dell’energia, delle sezioni d’urto di tali processi, si hanno corrispondentemente picchi di r., cioè massimi relativi alti e, in genere, stretti: di ognuno di questi picchi è caratteristico il valore dell’energia E corrispondente al valore massimo e al valore della larghezza Γ misurata a un’altezza pari alla metà del valore massimo. In prossimità di un picco di r. la sezione d’urto è descritta dalla formula di Breit e Wigner (➔ reazione).

R. stocastica

Fenomeno di sincronizzazione tra le transizioni indotte da un disturbo casuale (o rumore) e una perturbazione periodica nel tempo contenuta in un sistema. Il fenomeno della r. stocastica è stato osservato sperimentalmente in circuiti elettronici non lineari, nei laser ad anello, in esperimenti di risonanza paramagnetica e in nastri magnetoelastici. Alcuni esperimenti hanno rivelato il fenomeno della r. stocastica in sistemi biologici: singoli neuroni e fibre del nervo uditivo della scimmia, meccanorecettori situati nella coda di un gambero d’acqua dolce. Inoltre si sta approfondendo la ricerca allo scopo di utilizzare la r. stocastica per estrarre informazioni da un segnale in condizioni di basso rapporto segnale/rumore all’ingresso del sistema. La r. stocastica è stata anche utilizzata per l’ottimizzazione del flusso dell’informazione in modelli, ottenuti con reti neurali, per processi cognitivi (percezione multistabile).

Risonatori

Il risonatore è un dispositivo dotato della proprietà di entrare in regime di oscillazione soltanto se stimolato da sollecitazioni di frequenza prossima a quella di r., risultando invece praticamente insensibile a sollecitazioni di frequenza diversa. Risonatore elettrico Circuito elettrico capace di entrare in oscillazione per r. con un oscillatore: qualsiasi circuito oscillante, eccitato opportunamente, costituisce un risonatore elettrico. I circuiti oscillanti usati come risonatori possono essere a costanti concentrate, cioè costituiti da induttori e condensatori, o a costanti distribuite, costituiti, per es., da una coppia di fili di Lecher (risonatori a linee) o da una cavità (risonatori a cavità). I risonatori a costanti distribuite sono usati nel campo delle altissime frequenze (in genere da 300 MHz in su), nel quale i risonatori a costanti concentrate sono di difficile realizzazione; fra essi sono particolarmente usati i risonatori a cavità, costituiti da un corpo conduttore cavo (cavità risonante) riempito da un dielettrico (generalmente l’aria) omogeneo e di costanti note. Sono talora usati come risonatori elettrici anche i quarzi piezoelettrici (risonatori piezoelettrici; ➔ piezoelettricità): questi ultimi equivalgono a circuiti oscillanti estremamente selettivi e costituiscono pertanto dei risonatori ad altissimo fattore di merito. Anche il fenomeno della magnetostrizione (➔) può essere utilizzato per realizzare risonatori. Risonatore meccanico Ogni sistema meccanico è caratterizzato da una particolare frequenza di oscillazione propria, f (detta anche frequenza delle oscillazioni libere). Quando il sistema viene sollecitato da una forza esterna periodica di frequenza f, esso si porta in uno stato di risonanza. Viene detto risonatore meccanico un sistema costruito appunto per entrare in r. in corrispondenza di una o più prefissate frequenze di eccitazione f. Fra i risonatori meccanici rientrano i risonatori elastici, sistemi capaci di entrare in r. quando siano investiti da onde elastiche. Risonatore ottico Dispositivo all’interno del quale possono instaurarsi, con basse perdite, oscillazioni elettromagnetiche nella banda delle frequenze ottiche, generalmente costituito da due specchi, piani o sferici, affacciati.

Psicologia

Modo globale di percepire le forme a contenuto espressivo, con componente empatica e intuitiva.

Il tipo di r. interne è, nel test di H. Rorschach (➔), il modo di elaborazione degli stimoli ambientali, dipendente ora dall’attività intrapsichica ora dagli stimoli esterni, specie dal colore.