tensione
Fisica e tecnica
Il termine t. ha anzitutto il significato di forza, più precisamente di forza di trazione: così, si parla di t. applicate agli estremi di una sbarra, di una fune ecc. Con diverso significato, nella meccanica dei sistemi continui, è equivalente a sforzo specifico o a una componente di esso (➔ sforzo; elasticità); in particolare, t. interna (o t. residua), quella presente in un corpo, in assenza di forze esterne.
Il termine è più spesso usato quando si tratta di sforzi di trazione, ma anche con riferimento a sforzi tangenziali e talora alla pressione di un fluido. T. di vapore La pressione parziale a cui si trova un vapore saturo nell’ambiente che lo contiene. La t. di vapore Reid esprime la volatilità di un carburante ed è misurata dalla pressione parziale assunta dai vapori del carburante in esame quando questo è riscaldato in un recipiente standardizzato (bomba Reid) a 37,8 °C; è una caratteristica di cui in genere si richiede la specificazione per i prodotti petroliferi volatili.
Si dice che tra due corpi o tra due punti di un conduttore o di un circuito esiste una t. elettrica se esiste tra essi una differenza di potenziale elettrico, sicché i due termini t. e differenza di potenziale sono scambievolmente usati uno per l’altro. In analogia a quanto si fa in elettrotecnica, anche nel magnetismo si usa spesso il termine t. magnetica per indicare una differenza di potenziale magnetico scalare.
T. interfaciale (o interfacciale)
È la forza, riferita all’unità di lunghezza, che agisce tangenzialmente alla superficie di separazione fra due fasi di un sistema ed è orientata in direzione normale a ogni elemento lineare della superficie stessa. Esprimibile in N/m, è fisicamente equivalente all’energia libera interfaciale, esprimibile in J/m2. Se le fasi separate dall’interfase sono un liquido e un gas, la t. interfaciale prende il nome più specifico di t. superficiale. Come appare dalle tab. 1 e 2, la t. interfaciale tra due liquidi è minore della più grande fra le due t. superficiali, in quanto il numero di molecole per unità di volume è sempre maggiore in un liquido rispetto a un gas (nella proporzione 1000 : 1, orientativamente) e ciò diminuisce lo squilibrio nel bilancio delle forze attrattive per le molecole poste sull’interfase. In corrispondenza di un’interfase, in particolare di un’interfase liquido-liquido o liquido-gas, esiste infatti uno sbilanciamento delle forze intermolecolari cui sono soggette le molecole che si trovano in prossimità dell’interfase stessa: le molecole che si trovano all’interno di ciascuna fase sono mediamente soggette a uguali forze di attrazione che si manifestano in tutte le direzioni, mentre le molecole collocate all’interfase si trovano sotto l’azione di una forza non bilanciata.
Per i sistemi liquido-liquido conviene definire due importanti grandezze. Se si fa riferimento a un liquido, A, raccolto in un cilindro con sezione trasversale di 1 m2 e in corrispondenza a una generica sezione si divide il cilindro in due parti, si formano due nuove superfici liquido-gas, di area complessiva pari a 2 m2; il lavoro compiuto, pari a 2γA, dove γA è la t. superficiale del liquido, è definito come lavoro di coesione, Wc, del liquido A. Si consideri ora un sistema costituito da due liquidi diversi, A e B, raccolti in due cilindri, ciascuno con sezione trasversale di 1 m2, l’uno sovrapposto all’altro; se si separano i due cilindri, si creano due nuove superfici liquido-gas, ciascuna con area di 1 m2 e con la propria t. superficiale (γA e γB), e si annulla l’interfase di separazione fra i due liquidi, di area 1 m2 e di t. interfaciale γAB; il lavoro compiuto per separare i due cilindri è definito come lavoro di adesione, Wa, fra i due liquidi, pari a: Wa=γA+γB−γAB (equazione dovuta ad A. Dupré). Affinché il liquido A si possa allargare spontaneamente sul liquido B, occorre che il lavoro di adesione sia maggiore del lavoro di coesione del liquido che si spande; si definisce un coefficiente di dispersione, SAB, pari a Wa−Wc, ovvero: SAB=γB−γA−γAB. Affinché A si possa disperdere in B, occorre che SAB sia maggiore di zero; per SAB<0, A si raccoglie sotto forma di goccioline sulla superficie di B. L’equazione di Dupré si applica rigorosamente soltanto ai liquidi che possono considerarsi completamente immiscibili fra loro.
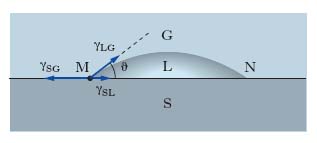
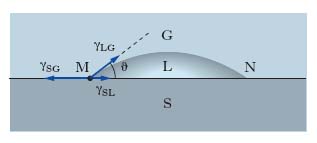
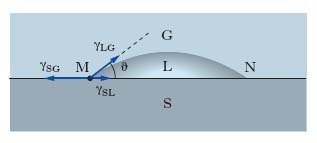
Nei sistemi costituiti da 3 fasi, per es., un solido (S), un liquido (L), un gas (G), non esiste una superficie, ma soltanto una linea di contatto; nel rappresentare un sistema siffatto su un piano (fig. 1), la linea di contatto è rappresentata dai suoi punti M e N di intersezione con il piano del disegno. Facendo riferimento, per es., al punto M, in esso devono farsi equilibrio le t. interfaciali γSG (sistema solido-gas), γLG (sistema liquido-gas) e γSL (sistema solido-liquido), ciascuna orientata nella direzione della superficie di contatto fra le due fasi corrispondenti e nel verso che si oppone a un aumento dell’interfase stessa. La relazione di equilibrio delle forze è: γSG=γSL+γLG cosϑ, dove ϑ prende il nome di angolo di contatto (o di raccordo); quanto minore è ϑ, tanto maggiore è la bagnabilità del solido da parte del liquido; la condizione di completa bagnabilità è data da ϑ=0. Le forze di t. interfaciale acquistano fondamentale importanza nell’interpretazione di svariati fenomeni biologici a livello chimico-fisico, quali l’adsorbimento di particolari molecole sulle membrane cellulari, la spiccata tendenza di sostanze ad attività superficiale di accumularsi alla interfase in accordo alla legge di Gibbs, e la riduzione dell’energia di attivazione che si verifica per diversi composti, per la seconda legge della termodinamica, alla superficie degli enzimi per cui è reso possibile lo svolgersi di importanti reazioni biochimiche.
T. superficiale
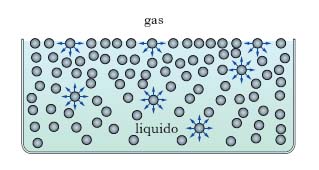
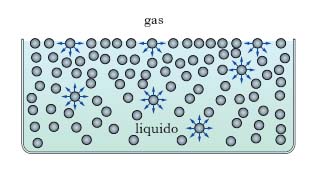
Come si è detto, è la t. interfaciale che agisce nel caso di un’interfase liquido-gas. L’origine della t. superficiale è ancora la distribuzione non bilanciata delle forze attrattive intermolecolari presentata in superficie dalle molecole di liquido, a differenza di quanto accade per le molecole poste all’interno, che sono simmetricamente circondate da altre molecole con conseguente bilanciamento delle forze intermolecolari (fig. 2). In fase gassosa, il numero assai minore di molecole per unità di volume rende trascurabile l’interazione con le molecole di liquido in superficie; così, sulla superficie del liquido si manifesta, nel complesso, una forza diretta verso l’interno in direzione normale alla superficie; pertanto, per aumentare l’area della superficie del liquido, occorre fornire energia in quanto è necessario un lavoro per portare molecole dalla massa del liquido fino alla superficie vincendo la forza di attrazione verso l’interno; l’energia necessaria ad aumentare dell’unità di area la superficie di un liquido prende il nome di energia libera superficiale e si esprime in J/m2. La naturale tendenza a contrarsi manifestata dalla superficie di un liquido al fine di rendere minima l’energia libera che compete alla superficie totale spiega perché la superficie stessa mostri il comportamento di una membrana tesa. A tal proposito si consideri sulla superficie liquida una maglia rettangolare, di lati a, b, con un lato che si sposti parallelamente a sé stesso di Δb, così da aumentare la superficie del liquido di aΔb; occorre fornire un’energia pari a EaΔb, essendo E l’energia libera superficiale che compete alla superficie. Il lavoro compiuto per aumentare la superficie può essere inteso come il prodotto di una forza F, diretta normalmente al lato mobile, per lo spostamento Δb; d’altra parte F=γa, indicando con γ la forza riferita all’unità di lunghezza; ne consegue: EaΔb=FΔb=γaΔb, cioè E=γ, e quest’ultima è la t. superficiale che compete alla superficie in esame. Tale t. è fisicamente equivalente all’energia libera superficiale, che dev’essere considerata come la grandezza fondamentale che regola i fenomeni superficiali. Alla t. superficiale è dovuto, fra l’altro, il fatto che i liquidi si raccolgono in gocce (alla conformazione sferica corrisponde la minima energia libera che compete alla superficie totale); l’assimilazione della superficie liquida a una membrana tesa per effetto della t. superficiale spiega perché un ago metallico non affonda nell’acqua, malgrado l’elevata densità, se appoggiato con cautela sulla superficie. Nella tab. 2 sono riportati i valori che a 20 °C competono alle t. superficiali di alcuni liquidi (la fase gassosa è aria satura del vapore del liquido considerato). Nel caso in cui la superficie di separazione liquido-gas non sia piana, per effetto della t. superficiale γ si origina in ogni punto P della superficie una pressione di curvatura, p, che dà luogo a forze dirette normalmente verso la parte concava della superficie, calcolabile con la relazione (dovuta a P.-S. Laplace):
ove R1, R2 sono i due raggi principali di curvatura della superficie in P; se la superficie è sferica e di raggio R, si ha p=2γ/R. La formula di Laplace trova importanti applicazioni, per es. nello studio dei fenomeni di capillarità. Una conseguenza dell’esistenza di una pressione di curvatura dovuta alla t. superficiale è che la t. di vapore τ′ di una goccia di liquido è maggiore della t. τ che compete allo stesso liquido quando presenta una interfase piana con la fase gassosa; vale infatti la relazione: log(τ′/τ)=2γM(rρRT), dove M è il peso molecolare del vapore, r il raggio della goccia, ρ la densità del liquido, R la costante dei gas perfetti, T la temperatura termodinamica. Un aumento di temperatura accresce il contenuto energetico delle molecole disposte sulla superficie di un liquido, diminuendo così la forza attrattiva diretta verso l’interno e, in conseguenza la t. superficiale; sussiste la relazione empirica: γ1/4/(ρ−ρ′)=C, dove ρ, ρ′ sono le densità, alla generica temperatura T, del liquido e del vapore, rispettivamente, e C è una costante per ogni sostanza.
Linguistica
In fonetica, t. articolatoria, e t. muscolare dell’articolazione, la t. della muscolatura dell’apparato di fonazione: varia con il variare dell’energia fonatoria e con il variare delle singole articolazioni (per es., -t- rispetto a -tt- ecc.).