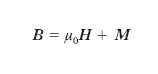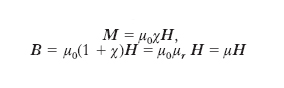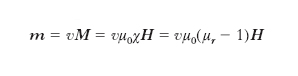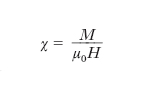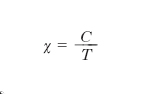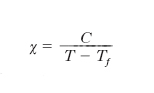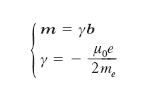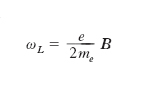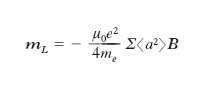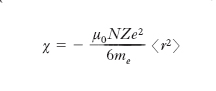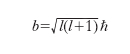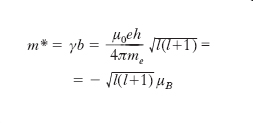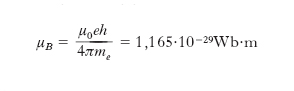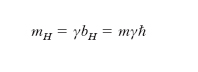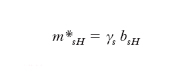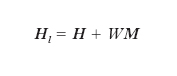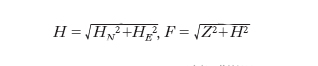magnetismo

fisica

L’insieme dei fenomeni fisici dovuti all’esistenza di un particolare campo di forza, il campo magnetico, che ha la sua origine in correnti elettriche e determina, attraverso i magneti, azioni meccaniche su corpi di ferro o di altre sostanze magnetizzabili, alcuni dei quali (per es. quelli ferrosi) acquistano proprietà simili, diventando quindi magneti artificiali.

La parte della fisica che si occupa dei fenomeni magnetici riguardanti le interazioni di magneti tra loro e con altri corpi, e i campi magnetici, costituenti la sede e, attraverso i loro vettori, la formalizzazione vettoriale di tali interazioni.

1. Sviluppo delle conoscenze

1.1 Le prime teorie. - Ai Greci e ai Romani era nota la proprietà di attrarre il ferro che hanno i magneti naturali (in particolare la magnetite); cognizioni più vaste e più precise sui fenomeni magnetici non si ebbero però per molto tempo. A J. Michell risale l’osservazione, confermata poi da altri studiosi, e con maggiore precisione da C.-A. de Coulomb, che le azioni attrattive o repulsive tra poli magnetici seguono una legge analoga a quella delle azioni tra corpi elettrizzati. Lo stesso Coulomb tentò una spiegazione dei fenomeni magnetici fondandola sull’ipotesi dell’esistenza di due fluidi, uno positivo e uno negativo, contenuti in quantità uguali in ogni ‘molecola’ di un corpo magnetizzato o magnetizzabile e, a differenza dei fluidi elettrici, confinati nella molecola in modo da non poter passare da una molecola all’altra. Nei magneti permanenti le due cariche di fluido opposto sarebbero localizzate ai due estremi della molecola; nei corpi magnetizzabili sarebbero invece libere di muoversi entro la molecola portandosi ai suoi estremi soltanto per effetto di speciali azioni.

1.2 La trattazione matematica dei fenomeni macroscopici del magnetismo. - La teoria di Coulomb diede lo spunto a una trattazione matematica, a opera di S.-D. Poisson (1820). Intanto, le scoperte di H.C. Oersted e di A.-M. Ampère rivelavano rapporti inattesi tra fenomeni magnetici e fenomeni elettrici. La costruzione di potenti elettromagneti diede a M. Faraday (1825-27) la possibilità di riconoscere che tutti i corpi sono in qualche modo capaci di risentire l’azione di un campo magnetico nel quale siano immersi in modo da divenire tutti, più o meno temporaneamente, dei magneti. Alcune sostanze, come l’alluminio, il cromo, il manganese e il platino si magnetizzano in modo tale che una barretta di tali sostanze posta in un campo magnetico non uniforme tende a disporsi parallelamente al campo: queste sostanze sono dette paramagnetiche. Altre sostanze invece, come lo zinco, lo zolfo, il mercurio, l’oro e soprattutto il bismuto, si magnetizzano in modo tale che una barretta di tali sostanze posta in un campo magnetico non uniforme tende a disporsi ortogonalmente al campo: queste sostanze sono dette diamagnetiche. Sia i corpi diamagnetici sia i paramagnetici si magnetizzano, a parità di condizioni, assai meno di talune sostanze, che sono dette ferromagnetiche in quanto esponente tipico è il ferro (tali sostanze sono, oltre al ferro, il nichel, il cobalto, il gadolinio e varie leghe metalliche). Abbandonata l’ipotesi dei fluidi, Ampère, avanzò l’ipotesi che il m. non è che una particolare manifestazione di un fenomeno elettrico, la magnetizzazione di ciascuna molecola essendo dovuta a una corrente permanente che circola nella molecola medesima (correnti elementari di Ampère, o correnti di magnetizzazione). Faraday, inoltre, rifiutandosi di concepire gli effetti magnetici come azioni a distanza, preferì considerarli come azioni locali mediate dal mezzo interposto, introducendo così il concetto di campo.

J.C. Maxwell mise successivamente in luce che, in una coerente teoria matematica del campo elettromagnetico, per trattare i fenomeni magnetici sono necessari due vettori H e B (detti rispettivamente intensità del campo magnetico e induzione magnetica) con proprietà e caratteristiche diverse, le sorgenti dell’uno essendo solo le correnti ‘localizzate’, mentre quelle del secondo sono anche le correnti di magnetizzazione. L’inquadramento teorico maxwelliano fu perfezionato da O. Heaviside, la cui opera segna per molti aspetti un punto d’arrivo nella trattazione matematica dei fenomeni macroscopici del m. e dell’elettromagnetismo. Nell’ambito della fisica classica tutti i fenomeni magnetici sono ricondotti a cariche elettriche in moto tra le quali si esplicano le azioni magnetiche.

1.3 L’interpretazione microscopica dei fenomeni magnetici. - Sono da ricordare, nell’ambito del m. classico, le ricerche di P. Curie, di J. Larmor e P. Langevin e di P.-E. Weiss. Curie (1895) dimostrò, fra l’altro, che le proprietà di una sostanza diamagnetica, in particolare la suscettività, sono indipendenti dalla temperatura; mentre la suscettività di una sostanza paramagnetica è legata alla temperatura termodinamica. Larmor e Langevin (1905) spiegarono il diamagnetismo come proprietà di origine atomica, comune a tutti i corpi, legata (come già era stato ipotizzato da H.A. Lorentz) al moto orbitale degli elettroni dell’atomo, mentre considerarono il paramagnetismo come un effetto che, ove si manifesti, sovrasta il diamagnetismo, dovuto a molecole dotate di un proprio momento magnetico permanente, capaci di orientarsi sotto l’azione di un campo magnetico esterno. La teoria di Weiss (1907), ricollegandosi a quella di Langevin ed estendendola, riuscì a dare un’esauriente interpretazione del ferromagnetismo. Dominante nella sua teoria è il concetto che una molecola dotata di momento magnetico, e quindi assimilabile a un ‘dipolo elementare’, risente non solo del campo ‘esterno’, ‘magnetizzante’, ma anche di un campo interno, molecolare, detto appunto di Weiss, generato dai circostanti dipoli elementari e proporzionale alla magnetizzazione. La teoria di Weiss permette di riconoscere che una magnetizzazione esiste sempre in ogni frammento di materiale anche quando sia nullo il campo esterno: è fenomeno della magnetizzazione spontanea. Il fatto che, malgrado ciò, i materiali ferromagnetici si presentino generalmente non magnetizzati è spiegato da Weiss con l’ipotesi dei domini, regioni molto piccole ma contenenti un gran numero di molecole, nelle quali l’intensità di magnetizzazione è la massima possibile a quella temperatura; tali domini sono disposti, in assenza di campo esterno, a caso, in modo che non è rilevabile macroscopicamente alcuna magnetizzazione. L’azione di un campo esterno, che si esercita dunque non sulle singole molecole, come nel caso delle sostanze paramagnetiche, ma sui domini, ha per effetto di orientare questi ultimi nella direzione del campo (senza mutare l’intensità di magnetizzazione del singolo dominio): compare così l’effetto macroscopico.

1.4 M. su basi quantistiche. - Nel 1932 J.H. van Vleck dimostrò che, applicando rigorosamente le teorie classiche, diamagnetismo e paramagnetismo di una sostanza dovrebbero annullarsi a vicenda e dunque la materia non potrebbe magnetizzarsi. Una corretta trattazione del m. può essere fatta solo su basi quantistiche. Applicando la meccanica quantistica risulta che è quantizzato non solo il momento magnetico orbitale dell’elettrone, quello cioè associato al moto di rivoluzione intorno al nucleo, ma anche, il momento magnetico intrinseco o ‘di spin’, che all’elettrone compete per il fatto di essere dotato di un momento della quantità di moto intrinseco o ‘di spin’ (ipotesi dell’elettrone rotante, G.E. Uhlenbeck e S.A. Goudsmit, 1925). Le teorie quantistiche spiegano esaurientemente la fenomenologia generale del m., anche per ciò che concerne l’antiferromagnetismo e il ferrimagnetismo, nonché molti fenomeni particolari, per es., l’effetto Zeeman (➔ Zeeman, Pieter).

2. Magnetostatica ed elettromagnetismo

fig. 1

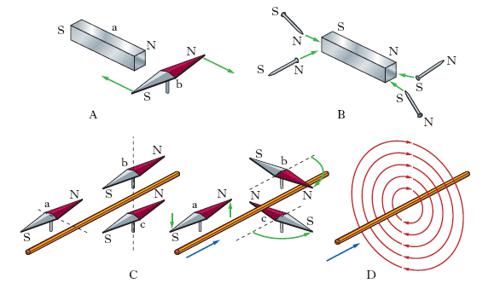
Seguendo uno schema storico-logico, le prime questioni che si presentano sono quelle relative a campi magnetici statici, cioè costanti nel tempo, e che nel complesso costituiscono la magnetostatica. Si tratta di campi che possono essere generati da magneti permanenti statici, in quiete e di momento magnetico costante nel tempo, ovvero da elettromagneti statici, cioè da circuiti di forma invariabile, in quiete e percorsi da una corrente di intensità costante (fig. 1). Il calcolo dell’intensità H del campo può farsi nel primo caso assimilando i magneti a dipoli magnetici e quindi usando le formule per il campo di dipolo (➔ dipolo); nel secondo caso servendosi della prima formula di Laplace (➔ elettromagnetismo). Un oggetto dotato di momento magnetico m (un magnete, un corpo materiale magnetizzabile, un circuito percorso da corrente) risente in un campo magnetostatico di azioni riducibili a una coppia, di momento m×H, che determina una rotazione, e, se il campo non è uniforme, anche a una forza di componenti ∂(m∙H)/∂x_i, che determina una traslazione. Più complessa è la situazione nel caso di campi non statici, per l’insorgere, a causa del fenomeno dell’induzione elettromagnetica, di campi elettrici variabili associati ai campi magnetici. Tali campi elettrici dipendono, come già le azioni elettromagnetiche, dall’induzione del campo, cioè dalle proprietà magnetiche del mezzo materiale in cui si svolge il campo; a tali fenomeni è anche riconducibile la particolare condizione in cui si trova un corpo magnetizzato.

3. Proprietà magnetiche della materia

L’esperienza mostra che tutte le sostanze, sia pure in modo e in grado diversi, si magnetizzano sotto l’azione di un campo magnetico in cui siano immerse, acquistando un momento magnetico. Si dà il nome di intensità di magnetizzazione alla grandezza vettoriale, M, rappresentante il momento magnetico dell’unità di volume di una sostanza magnetizzata; l’unità di misura per M è quella stessa dell’induzione magnetica, cioè, nel Sistema Internazionale, il Wb/m² o tesla (simbolo T). Se H è l’intensità del campo magnetizzante, l’induzione B nella sostanza vale, sempre in unità del SI,

[1] formula,

dove μ₀ è la permeabilità magnetica assoluta del vuoto (4π∙10^–7 H/m); poiché la magnetizzazione dipende dal campo magnetizzante e M e μ₀H sono quantità equidimensionate, si può porre

,

dove χ e μ_r sono grandezze adimensionate, dette, rispettivamente, suscettività magnetica e permeabilità magnetica relativa, e μ, grandezza dimensionata, è la permeabilità magnetica assoluta della sostanza. Il momento magnetico di un corpo uniformemente magnetizzato vale

,

essendo v il volume; da questo momento dipendono sia il campo generato dal corpo nello spazio circostante sia le azioni che esso risente da parte di altri campi. Le proprietà magnetiche di una sostanza sono pertanto completamente determinate da χ oppure da μ_r, che in genere dipendono, oltre che dalla natura della sostanza, dalla temperatura e, per certe sostanze, anche dall’intensità del campo magnetizzante: si tratta di grandezze scalari in caso di mezzi isotropi, di grandezze tensoriali nel caso di mezzi anisotropi.

La suscettività viene definita, per un mezzo omogeneo e isotropo, dalla relazione

[2] formula.

Effettuando misurazioni di suscettività in varie condizioni di temperatura e di campo magnetizzante, si riconosce che le sostanze possono essere raggruppate, dal punto di vista del comportamento magnetico, in 5 categorie.

tab. 1

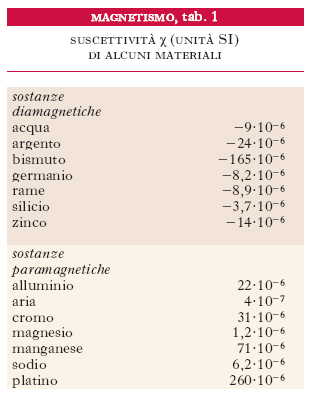
Le sostanze diamagnetiche presentano suscettività negativa, di piccolo valore (10⁻⁵-10⁻⁴), indipendente dalla temperatura termodinamica T e da H: esse si magnetizzano debolmente in verso opposto al campo magnetizzante. L’acqua pura e i gas nobili appartengono a questa categoria (tab. 1).

Le sostanze paramagnetiche hanno suscettività positiva, di piccolo valore (10⁻⁶-10⁻⁴), indipendente da H, ma dipendente da T secondo la relazione (legge di Curie):

[3] formula,

dove C è una costante positiva caratteristica di ciascuna sostanza, detta costante di Curie. Tali sostanze si magnetizzano debolmente in verso concorde con quello del campo magnetizzante. Paramagnetici sono in genere i gas (esclusi i gas nobili); il valore estremamente piccolo della suscettività magnetica dell’aria è tale da poter lecitamente assimilare l’aria al vuoto in molte questioni pratiche.

Le sostanze ferromagnetiche hanno suscettività positiva, di valore alto (sino a 10⁶) ma estremamente dipendente da H e da T. La dipendenza dalla temperatura si traduce, per queste sostanze (Fe, Ni, Co, Gd e varie leghe), nel fatto che al di sopra di una certa temperatura T_f (temperatura di Curie ferromagnetica) χ dipende da T secondo la legge di Curie-Weiss:

[4] formula,

fig. 2

tab. 2

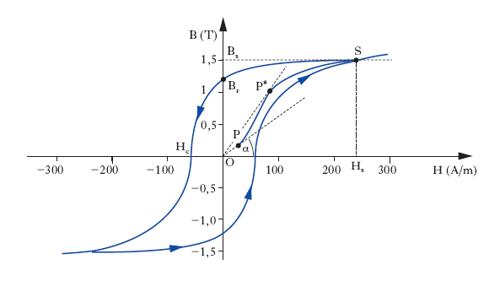
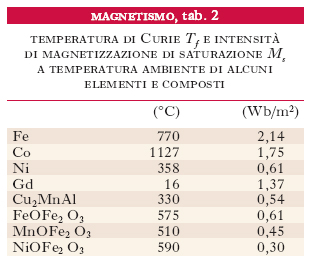
dove C è la costante di Curie della sostanza. Al di sotto della temperatura T_f, la dipendenza di χ da T è piuttosto complessa e non esprimibile con una relazione analitica. L’andamento di χ al variare di H, al di sotto della temperatura T_f, è deducibile dalla cosiddetta curva di magnetizzazione della sostanza, che è il diagramma dell’induzione B in funzione di H e ha, in relazione alle varie vicende della magnetizzazione, l’aspetto tipico mostrato nella fig. 2. L’origine O corrisponde allo stato della sostanza non magnetizzata precedentemente e in assenza di campo magnetizzante; applicando quest’ultimo e facendone crescere l’intensità H, B, inizialmente nulla, cresce seguendo la curva di prima magnetizzazione, O P P*S, sempre più lentamente, sino a portarsi su un valore B_s, che resta poi pressoché costante (induzione di saturazione): si è raggiunta la condizione di saturazione magnetica della sostanza. In realtà ciò che resta costante in condizioni di saturazione non è esattamente l’induzione B, ma l’intensità di magnetizzazione M, che effettivamente raggiunge un certo valore M_s (magnetizzazione di saturazione) e non lo supera anche se H cresce indefinitamente. La suscettività data dalla [2] è proporzionale alla tangente dell’angolo α che la congiungente l’origine con il generico punto P della curva di prima magnetizzazione forma con l’asse H; raggiunge dunque un valore massimo quando tale congiungente è tangente alla curva (punto P*), dopo di che decresce; in regime di saturazione si ha, dalla [2], che χ è inversamente proporzionale ad H, riducendosi a zero al crescere indefinito di H. Se, raggiunta la saturazione, si fa decrescere H, anche B decresce, tuttavia in ritardo, con ‘isteresi’ rispetto ad H: infatti quando H si annulla, B è non nullo, conservando un valore, B_r (induzione residua), pari, per la [1], alla magnetizzazione residua, M_r, della sostanza. In concreto, rimuovendo il campo magnetizzante la sostanza resta magnetizzata (per le sostanze dia- e paramagnetiche, la magnetizzazione invece si annulla all’annullarsi del campo magnetizzante). Per annullare l’induzione in una sostanza ferromagnetica precedentemente magnetizzata occorre applicare un campo di opportuna intensità e diretto in verso opposto a quello che aveva magnetizzato la sostanza; tale campo, e anche la corrispondente intensità, H_c, ha il nome di campo coercitivo. Aumentando l’intensità di questo campo smagnetizzante, si produce una magnetizzazione in verso opposto a quella precedente, raggiungendosi un’opposta condizione di saturazione magnetica; e così via. In definitiva, facendo variare ciclicamente H tra due valori uguali e opposti, maggiori e uguali, in valore assoluto, a H_s, si ottiene una curva di magnetizzazione chiusa (fig. 2), da immaginarsi percorsa ciclicamente, che ha il nome di ciclo d’isteresi magnetica. Al di sopra della temperatura di Curie, χ è indipendente da H, così come avviene nelle sostanze paramagnetiche (tab. 2).

Le sostanze ferrimagnetiche comprendono alcune sostanze naturali, quali la magnetite, e artificiali, le cosiddette ferriti, il cui comportamento generale è simile a quello delle sostanze ferromagnetiche. I valori dell’induzione di saturazione sono peraltro più bassi (0,1-0,5 Wb/m² contro 0,3-2,5 Wb/m²) e l’andamento di χ con T al di sopra della temperatura di Curie è diverso da quello rappresentato dalla [4], cioè dalla legge di Curie-Weiss.

Le sostanze antiferromagnetiche (specialmente composti del manganese e del cromo) hanno comportamento simile a quello delle sostanze paramagnetiche, salvo che l’andamento di χ con la temperatura termodinamica T presenta una discontinuità in corrispondenza di un certo valore T_N di T, detto temperatura di Néel o di transizione: al di sotto di T_N la funzione χ(T) è crescente, mentre al di sopra è decrescente.

4. Teoria classica del diamagnetismo e del paramagnetismo

Si è in precedenza accennato che nelle teorie classiche del m. le proprietà magnetiche delle molecole vengono fatte derivare unicamente dal momento magnetico che si deve attribuire a ogni elettrone in conseguenza del suo moto orbitale intorno al nucleo. In effetti, un elettrone in moto sulla sua orbita equivale a tutti gli effetti a una minuscola spira percorsa da una corrente la cui intensità i è pari al prodotto della carica dell’elettrone, −e, per la frequenza del moto orbitale; assimilando quest’ultimo, come con buona approssimazione si può fare, a un moto circolare uniforme, di raggio r e velocità angolare ω, è i =−eω/2π. Per il principio di equivalenza di Ampère, tale ‘spira elettronica’, di area πr², ha un momento magnetico m pari a −(μ₀er²/2)ω, ovvero, facendo intervenire il momento della quantità di moto, b = m_er×v, pari a −(μ₀e/2m_e)b, m_e essendo la massa dell’elettrone; si può in definitiva scrivere:

[5] formula,

fig. 3

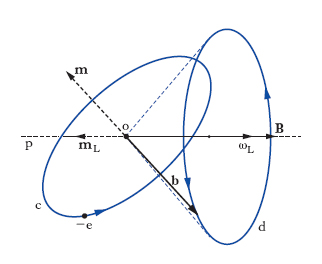
essendo γ il cosiddetto rapporto magnetomeccanico (molti autori danno a γ il nome di rapporto giromagnetico, che invece è normalmente definito come l’inverso di γ). Vi è dunque proporzionalità tra momento magnetico e momento della quantità di moto dell’elettrone; i due vettori, peraltro, sono antiparalleli, in virtù del segno negativo che compete al coefficiente di proporzionalità γ. Il momento magnetico complessivo di una molecola è il risultante dei singoli momenti elettronici. In alcuni elementi o composti le molecole hanno momento risultante nullo, in altri invece hanno momento diverso da zero; nel secondo caso, si dice che la molecola ha un momento magnetico proprio. Immaginiamo ora che su un atomo agisca un campo magnetico e consideriamo un elettrone e percorrente un’orbita c comunque inclinata rispetto all’induzione B del campo (fig. 3); alla forza coulombiana esercitata dal nucleo si aggiunge la forza di Lorentz dovuta al campo; come si riconosce (teorema di Larmor), insorge un moto di precessione del piano orbitale intorno a un asse p (asse della precessione) parallelo a B e passante per il centro o dell’orbita, con una velocità angolare (velocità angolare della precessione di Larmor)

[6] formula;

è come se il momento della quantità di moto, b, che resta invariato in modulo, mutasse regolarmente di orientamento, descrivendo intorno a p il moto d indicato nella fig. 3 (la situazione è analoga a quella che si verifica quando si perturba la rotazione di un giroscopio). A questo moto di precessione è associato un momento della quantità di moto b_L = m_e‹a²›ω_L, dove ‹a²› è il valore quadratico medio della distanza a dell’elettrone dall’asse della precessione, e quindi un momento magnetico γb_L. Se si ripete lo stesso ragionamento per ognuno degli Z elettroni di un atomo (Z è il numero atomico), e si tiene conto delle [5], [6], si arriva, per il momento magnetico complessivo m_L dovuto a questo effetto del campo, alla relazione

Se si ammette che in media la distribuzione della carica elettronica sia a simmetria sferica, si trova che è Σ‹a²› = 2‹r²›/3, dove ‹r²› indica il valore quadratico medio del raggio delle orbite elettroniche. Se le molecole non hanno un momento magnetico proprio, non vi sono da considerare altri effetti del campo. L’intensità di magnetizzazione è pari al prodotto del momento m_L, antiparallelo rispetto al campo, acquistato da ogni singola molecola per il numero N di molecole contenute nell’unità di volume; per la suscettività χ si ha dunque, applicando la [2]:

[7] formula.

Secondo tale relazione, dovuta a Langevin, la suscettività delle sostanze le cui molecole non hanno un momento magnetico proprio è dunque una quantità negativa, costante in senso stretto, indipendente in particolare dalla temperatura e dal campo magnetizzante: è quanto l’esperienza ci dà per le sostanze diamagnetiche. Se invece le molecole hanno un momento proprio, m, l’azione del campo si esplica anche in coppie orientatrici sulle molecole, che tendono a disporsi in modo che il loro momento risulti parallelo all’intensità H del campo magnetizzante, in ciò contrastate dall’agitazione termica. La teoria, dovuta anche in questo caso a Langevin, ritrova la legge di Curie, [3], con C=Nm²/3kμ₀, essendo k la costante di Boltzmann e N il numero di molecole per unità di volume. Il fatto che per queste sostanze i risultati sperimentali siano quelli che si ricavano dalla teoria in base a soli effetti di orientamento delle molecole sta a significare che per le molecole dotate di momento proprio il diamagnetismo, che pure si produce, è del tutto trascurabile.

5. Teoria quantistica del diamagnetismo e del paramagnetismo

Nella teoria quantistica del magnetismo accanto ai momenti magnetici orbitali degli elettroni si deve tener conto anche dei loro momenti magnetici intrinseci o di spin, oltre naturalmente al fatto che i momenti magnetici risultano quantizzati sia in modulo sia in direzione (quantizzazione spaziale). Per il momento della quantità di moto orbitale di un elettrone in un atomo risulta

,

essendo ℏ la costante di Planck divisa per 2π e l il numero quantico orbitale che può variare per interi positivi tra zero e il valore del numero quantico principale n; al momento della quantità di moto orbitale è associato, ancora secondo la [5], un momento magnetico orbitale

[8] formula,

in cui il segno meno sta a ricordare che m* e b sono antiparalleli. Come si vede, si può assumere come unità di misura per questi momenti magnetici la quantità

[9] formula,

che ha il nome di magnetone di Bohr (esso rappresenta il momento magnetico orbitale dell’elettrone dell’atomo di idrogeno nello stato fondamentale). La quantizzazione spaziale consiste nel fatto che b (e di conseguenza m*) può assumere nello spazio solo alcune determinate direzioni o, ciò che è lo stesso, in presenza di un campo magnetico H la componente b_H di b secondo la direzione del campo può assumere soltanto i valori b_H = mℏ, m essendo il numero quantico magnetico che può assumere i (2l + 1) valori interi tra −l e +l (zero compreso); di conseguenza per la componente di m secondo il campo si ha

Analogamente per il momento della quantità di moto intrinseco o di spin b_s si ha b_sH = sℏ = ± ℏ/2, s essendo il numero quantico di spin che può valere ±1/2; per il momento magnetico intrinseco o di spin associato si ha

[10] formula,

dove il rapporto magnetomeccanico di spin è diverso da quello orbitale γ.

Sulla base della precessione dei momenti orbitali e di spin intorno alla direzione del campo magnetico, la teoria quantistica, dando conto tra l’altro del fatto che il diamagnetismo è proprietà caratteristica di atomi o di ioni ad anelli elettronici completamente occupati, giunge per la suscettività a una relazione che è sostanzialmente quella già data dalla teoria classica, cioè la [7].

Per quanto riguarda lo studio quantistico del paramagnetismo, anche in questo caso la trattazione è analoga a quella classica di Langevin, però con l’importante differenza che l’orientamento delle molecole nel campo magnetizzante, e quindi l’energia potenziale dei momenti propri molecolari, non possono essere qualunque, ma sono determinati da regole di quantizzazione.

6. Ferromagnetismo

Le molecole delle sostanze ferromagnetiche hanno, come quelle delle sostanze paramagnetiche, un momento magnetico proprio ma, a differenza di quelle, interagiscono fortemente tra loro; ciò significa che la teoria del loro comportamento può essere fatta seguendo le linee della teoria del paramagnetismo, a patto di tener conto che il campo agente sulla singola molecola (campo locale), H_l, è il risultante di quello magnetizzante esterno, H, e del campo molecolare (campo di Weiss), interno, WM essendo W una costante caratteristica di ogni sostanza, avente le dimensioni dell’inverso di una permeabilità assoluta e detta costante di Weiss:

[11] formula.

Quanto abbiamo detto può brevemente riassumersi affermando che nelle sostanze ferromagnetiche la costante di Weiss, trascurabile nelle sostanze paramagnetiche, ha valori cospicui (2,8∙20⁶ m/H per il ferro; 1,1∙10⁷ m/H per il nichel). Il fatto più importante da spiegare è l’esistenza della magnetizzazione residua, e, più in generale, del ciclo di isteresi magnetica. Una spiegazione di ciò è data dalla teoria di Weiss (1907), ricordata all’inizio, e basata sull’ipotesi dei domini; tale spiegazione, tuttavia, nulla dice sul meccanismo in virtù del quale si desta la magnetizzazione e sulla natura delle interazioni tra domini. Il punto di partenza delle teorie moderne è comunque il fatto, dimostrato da W. Heisenberg già nel 1929, che le interazioni molecolari responsabili del campo molecolare e, in definitiva, della formazione dei domini, sono forze di scambio, come tali derivanti da stati particolari di elettroni (analizzando tali interazioni si ottiene, tra l’altro, un’espressione per il calcolo a priori della costante di Weiss); a partire da tale ipotesi si sono costruite varie teorie, in alcune delle quali gli elettroni responsabili del ferromagnetismo sono considerati localizzati nei singoli atomi, mentre in altre essi sono considerati liberi, come elettroni di conduzione: le teorie del primo tipo danno conto abbastanza bene del comportamento del ferro, e di altre sostanze che si magnetizzano analogamente al ferro, mentre le teorie del secondo tipo si applicano bene al nichel e alle sostanze magneticamente simili al nichel. Queste teorie sono in grado di spiegare soddisfacentemente sia i fatti fondamentali del ferromagnetismo sia la maggior parte dei fatti più minuti.

Soddisfacente è, in particolare, la spiegazione che si ottiene per il comportamento dei domini sotto l’azione del campo magnetizzante. I processi fondamentali sono tre. Il primo (espansione reversibile dei domini) consiste nel fatto che quelli tra i domini che hanno una magnetizzazione propria quasi parallela al campo magnetizzante tendono ad aumentare il loro volume, mentre il contrario accade per i domini orientati circa antiparallelamente rispetto al campo. Tale processo è reversibile se le variazioni di volume sono piuttosto piccole, cioè se le deformazioni sono elastiche e non plastiche; resta così spiegata, in particolare, la magnetizzazione reversibile che si verifica nel primo tratto della curva di prima magnetizzazione (fig. 2), corrispondente appunto a espansioni reversibili dei domini. Proseguendo l’espansione dei domini, a un certo punto, superata una barriera di potenziale dovuta alle varie forme di energia in gioco (di scambio, cristallina, magnetoelastica), i domini a magnetizzazione favorevole si estendono bruscamente e irreversibilmente a spese di quelli vicini, in modo da formare domini di volume maggiore la cui magnetizzazione ha una direzione prossima a quella del campo agente (espansione irreversibile dei domini). È notevole la circostanza che le espansioni irreversibili non si producono con continuità, ma ciascuna bruscamente. Come terzo processo si ha la rotazione dei domini così formati, che tendono a disporsi nella direzione del campo magnetizzante, in ciò ostacolati da interazioni di scambio (interazioni di parete) che si hanno sulle superfici di separazione (pareti) tra domini contigui; tale rotazione è un fenomeno reversibile e continuo. Si hanno in definitiva due processi reversibili (di espansione iniziale, di rotazione in prossimità della saturazione) e un processo irreversibile (di espansione). Quest’ultimo è la causa dell’isteresi e della magnetizzazione residua; esso è anche la principale causa della spesa di energia che occorre nel processo globale di magnetizzazione, e che si ritrova in calore nel corpo magnetizzato; come si dimostra, l’energia spesa in un ciclo d’isteresi completo è proporzionale all’area del ciclo medesimo e al volume del corpo magnetizzato.

7. Antiferromagnetismo e ferrimagnetismo

Il comportamento delle sostanze antiferromagnetiche (pressoché paramagnetico agli effetti dei valori della suscettività e dell’intensità di magnetizzazione) e quello delle sostanze ferrimagnetiche (sostanzialmente ferromagnetico) è collegabile al precedente meccanismo di interazioni di scambio che dà luogo al ferromagnetismo. Mentre però in quest’ultimo le interazioni portano ad allineare tutti i momenti atomici parallelamente tra loro, nel caso dell’antiferromagnetismo si hanno interazioni di tipo particolare (interazioni di superscambio) che portano, per alcuni atomi, a un allineamento antiparallelo rispetto ad atomi contigui (accoppiamento antiferromagnetico): si crea così una struttura assimilabile a due reticoli compenetrantisi, in ciascuno dei quali tutti i momenti atomici o ionici sono allineati, le direzioni di magnetizzazione spontanea dei due reticoli essendo antiparallele tra loro. Questo schema, proposto da L. Néel nel 1936, dà soddisfacentemente conto dell’assenza di magnetizzazione spontanea globale, nonché dell’esistenza di una temperatura di transizione. Al crescere della temperatura, infatti, le interazioni antiferromagnetiche perdono di efficacia e la suscettività paramagnetica cresce, finché a un certo punto c’è il collasso della struttura antiferromagnetica, le molecole ritornano praticamente libere e si ha un normale comportamento paramagnetico (la suscettività decresce con la temperatura). Quanto alle sostanze ferrimagnetiche, la situazione è in un certo senso simile, cioè vi è una disposizione antiparallela dei momenti atomici, salvo che stavolta i momenti dell’uno e dell’altro reticolo sono disuguali; ciò spiega l’esistenza di una magnetizzazione spontanea e quindi di proprietà generali ferromagnetiche e, al tempo stesso, certe deviazioni rispetto al ferromagnetismo vero e proprio.

8. Fenomeni di risonanza magnetica

L’azione di un campo magnetico variabile nel tempo provoca su un sistema magnetico una perturbazione che dipenderà in generale sia dal meccanismo di eccitazione sia da quello di rilassamento. La trattazione del problema è analoga in linea di principio per i momenti magnetici associati ai nuclei (risonanza magnetica nucleare; ➔ anche risonanza) e per i momenti magnetici associati agli elettroni appartenenti sia a sistemi paramagnetici (risonanza paramagnetica elettronica) sia a sistemi magnetici ordinati (risonanza ferromagnetica, antiferromagnetica e ferrimagnetica). Ricorrendo a una descrizione classica, ricordiamo che per un sistema meccanico vale fra momento angolare P e momento torcente K la relazione dP/dt=K. Nel caso di un sistema costituito da nuclei o da elettroni vi è, inoltre, proporzionalità fra il momento angolare totale I e il momento magnetico totale M. Risulta M=γℏI, dove γ è il rapporto magnetomeccanico e ℏ la costante di Planck divisa per 2π. Infine il momento torcente in presenza di un campo d’induzione magnetico B vale M×B. Pertanto in presenza di un campo magnetico costante d’induzione B₀ sarà valida la relazione dM/dt=M×B₀ che indica una precessione di M attorno a B₀ con velocità angolare ω₀=γB₀. Se supponiamo che B₀ sia parallelo all’asse z, all’equilibrio termico la magnetizzazione sarà anche orientata lungo l’asse z e avrà un certo valore M₀. Si avrà pertanto M_x=0; M_y=0; M_z=M₀. Il moto è simile a quello di un oscillatore armonico smorzato. In assenza di rilassamento il vettore magnetizzazione precederebbe indefinitamente attorno a B₀ con velocità angolare ω₀. A causa del rilassamento la magnetizzazione spiralizza invece attorno a B₀. Un campo magnetico alternato, ortogonale a B₀, cederà energia al sistema quando la sua pulsazione ω₁ sarà uguale a ω₀ (risonanza). L’energia assorbita viene dissipata nel sistema sia mediante l’eccitazione di modi di vibrazione del reticolo sia anche mediante l’eccitazione di modi magnetici.

geologia

M. terrestre L’insieme dei fatti sperimentali e delle questioni teoriche che riguardano l’esistenza, la misurazione e lo studio del campo magnetico terrestre, e anche la parte della geofisica che si occupa di tali problemi.

1. Cenni storici

L’esistenza del campo magnetico terrestre è denunciata dalla proprietà che ha un ago magnetico, mobile attorno a un asse baricentrale, verticale, di indicare la direzione del Nord. Questa proprietà è nota sin da tempi antichissimi e di essa ci si giovò per realizzare dispositivi (bussole magnetiche) che indicassero il Nord; ma, a prescindere da alcuni passi di opere cinesi, peraltro di dubbia interpretazione, secondo i quali pare che i navigatori cinesi usassero una sorta di bussola già qualche secolo prima dell’era volgare, i primi documenti storici sull’uso degli aghi calamitati nelle bussole datano dal 1100. È di quell’epoca un manoscritto cinese nel quale è contenuta l’affermazione che l’ago magnetico non si dirige esattamente verso il Nord, ma a qualche grado da esso. L’esistenza della declinazione magnetica fu riscoperta più tardi (1492) da C. Colombo nel suo viaggio verso l’America. Per molto tempo ancora sfuggì tuttavia l’essenza del fenomeno; i naturalisti spiegavano il funzionamento della bussola come causato da azioni attrattive esercitate sull’ago da parte di grandi masse ferrose situate in una impreci;sata regione del Nord. Intorno al 1600 W. Gilbert avanzò per primo l’ipotesi, rivelatasi poi accettabile, che la Terra stessa fosse una grande calamita, magnetizzata secondo l’asse polare, in ciò persuaso, fra l’altro, dalla scoperta dell’inclinazione magnetica fatta (1544) dal tedesco G. Harmann. Costruito un magnete di forma sferica che chiamò ‘terrella’, avvicinando ad esso un piccolo ago calamitato Gilbert scoprì, fatto notevole per quei tempi, che l’inclinazione doveva aumentare dall’equatore ai poli e, inoltre, che la variabilità della declinazione da luogo a luogo poteva esser dovuta a inomogeneità della Terra. Dopo Gilbert molti astronomi, fisici, matematici hanno legato il loro nome ai problemi del m. terrestre: fra gli altri, H. Gellibrand, E. Gunter, E. Halley, J.C. Wilcke, K.F. Gauss, W.E. Weber, J. Lamont e, nell’età contemporanea, A. Schmidt, A. Schuster, S.J. Barnett, J.A. Bartels, S. Chapman.

2. Elementi magnetici e campo geomagnetico di dipolo

fig. 4

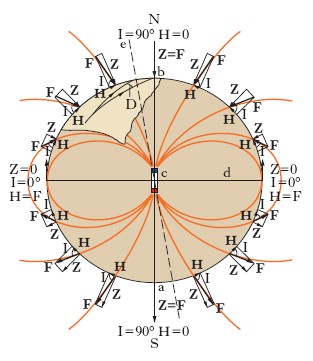
Gli studi condotti sul m. hanno evidenziato che un dipolo magnetico, libero di muoversi sulla Terra, si orienta in modo tale che la sua polarità magnetica nord sia rivolta verso il Nord geografico e la sua polarità magnetica sud verso il Sud geografico. Questo orientamento è legato all’esistenza di un campo magnetico terrestre, le cui linee di forza sono schematizzate in fig. 4 e che, in prima approssimazione, può considerarsi generato da un dipolo situato al centro della Terra che ha la sua polarità magnetica nord in prossimità del Sud geografico e la sua polarità magnetica sud in prossimità del Nord geografico. Per convenzione si è tuttavia deciso che i nomi dei poli magnetici terrestri siano invertiti e vengano chiamati con il nome dei poli geografici vicini.

fig. 5

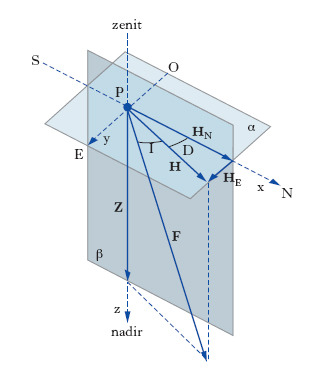
I tre elementi magnetici che servono all’individuazione del campo magnetico terrestre sono: il modulo del vettore intensità (F); l’inclinazione magnetica (I); la declinazione magnetica (D); questi elementi vengono riferiti a una terna cartesiana di riferimento (fig. 5) variabile da punto a punto e avente l’origine nel punto P in esame. Di questa terna, l’asse x giace nel piano orizzontale α ed è diretto verso il Nord geografico; l’asse y giace pure nel piano orizzontale α ed è diretto verso l’Est geografico; l’asse z giace nel piano verticale β ed è diretto verso il basso. Un dipolo magnetico esterno situato in un punto P, sulla superficie terrestre si dispone quindi in direzione tangenziale alle linee di forza del campo magnetico terrestre (F). L’angolo che questa direzione forma con le linee di forza di F prende il nome di inclinazione magnetica (I). Essa può essere negativa o positiva in relazione al fatto che il polo nord del dipolo sia rivolto rispettivamente verso l’esterno o verso l’interno della superficie terrestre. Il valore di I varia quindi tra +90° e −90°; questi due punti coincidono con i poli magnetici, mentre i punti dove I è uguale a 0 coincidono con l’equatore magnetico. La distribuzione di I sulla superficie terrestre può essere rappresentata con delle carte dove sono riportate le linee che uniscono tutti i punti della Terra nei quali I ha lo stesso valore (isocline). Lo stesso dipolo magnetico esterno nel punto P si orienta inoltre in modo tale da formare un angolo fra il meridiano geografico (coincidente in fig. 5 con il piano β) e il meridiano magnetico (coincidente con il piano verticale). Questo angolo definisce la declinazione magnetica (D); essa è positiva se il nord del dipolo si orienta verso l’Est geografico e negativa se si orienta verso ovest. La declinazione varia quindi da +180° verso E a −180° verso O. Anche la distribuzione di D può essere rappresentata sulla superficie terrestre con delle carte dove sono riportate delle isolinee (isogone) che hanno tutti i punti in cui il valore di D è uguale. L’intensità F del campo magnetico terrestre è generalmente espressa in gamma, γ, pari a 10^–5 oersted. Il vettore F può essere rappresentato tramite le sue due componenti: verticale (Z) e orizzontale (H) (fig. 5). La prima è coincidente con l’asse z dell’asse cartesiano ed è diretta verso il basso, verso l’interno della Terra; la seconda giace nel piano orizzontale α (piano topografico) ed è diretta verso il Nord geografico. Per queste due componenti si hanno le seguenti relazioni: Z=F∙senI; H=F∙cosI. La componente orizzontale può ulteriormente suddividersi lungo le direzioni geografiche N-S (H_N) ed E-O (H_E) assumendo come versi positivi quelli verso N ed E. Le due componenti di H possono essere così espresse: H_N=F∙cosI∙cosD; H_E=F∙cosI∙senD. Sia H che F possono inoltre essere espresse dalle seguenti relazioni:

Come per la declinazione e l’inclinazione magnetica, la distribuzione del modulo F sulla superficie terrestre può essere rappresentata su carte sempre mediante isolinee (isodinamiche) che uniscono tutti i punti dove F ha lo stesso valore.

Il vettore F aumenta con l’aumentare della latitudine; ha un valore minimo di 25.000 γ in corrispondenza dell’equatore (costa orientale dell’America Meridionale), un valore medio di 35.000 γ ai tropici (Indonesia) e di 70.000 γ in vicinanza del polo Nord magnetico. Per quanto riguarda l’Italia, l’intensità F del campo va da 46.500 γ al Brennero a 44.000 γ in Sicilia; la componente orizzontale varia tra 21.500 γ al Brennero e 27.000 γ in Sicilia; la declinazione è compresa tra 1° e 2° verso W; l’inclinazione va da circa 63° nell’Italia settentrionale a circa 52° in Sicilia.

Le misurazioni del campo magnetico terrestre indicano che questo in prossimità della Terra è descritto con buona approssimazione (➔ anche magnetosfera) dal campo geomagnetico di dipolo o campo di Gauss, generato da un dipolo magnetico posto al centro della Terra, di momento magnetico pari a 8,02∙10²⁵ u.e.m., e avente l’asse inclinato di 11,7° rispetto all’asse di rotazione. I punti in cui l’asse di questo dipolo incontra la superficie terrestre sono detti poli geomagnetici, o poli analitici, o poli di Gauss; in essi il campo dovuto ai soli termini di dipolo è parallelo all’asse del dipolo, ed ‘entrante’ al polo geomagnetico Nord, ‘uscente’ al polo geomagnetico Sud. I due poli si trovano rispettivamente a 78,3° N, 69,0° O e 78,3° S, 111,0° E. Il cerchio massimo passante per il centro del dipolo e normale al suo asse è l’equatore geomagnetico. In analogia con le coordinate geografiche si definiscono le coordinate geomagnetiche (➔ coordinate), con riferimento ai poli e all’equatore geomagnetici.

3. Variazioni del campo magnetico terrestre

3.1 Variazione secolare. - In un punto qualsiasi della Terra il valore degli elementi magnetici varia con il tempo; si chiama variazione secolare di un elemento magnetico il valore medio della sua variazione annua in un intervallo di 10 anni. Vi è una lenta variazione nel momento del dipolo: nel corso del 20° sec. esso è diminuito di circa il 5% del suo valore. Se si tracciano le carte del campo residuo per varie epoche, si trova che esse sono leggermente diverse da epoca a epoca; le differenze consistono sia in deformazioni delle linee isodinamiche, sia in un progressivo spostamento verso ovest di tali linee, spostamento che avviene in ragione di circa 0,18° all’anno. Se inoltre si tracciano le linee che uniscono i punti in cui si ha la stessa variazione annuale di una determinata componente (linee isopore), si ottengono dei sistemi di curve chiuse, di forma pressoché ovale, nel cui centro (fuoco isoporico) si ha la massima variazione, che per le componenti H e Z può giungere fino a circa ±100 γ all’anno. Anche questi sistemi di isopore presentano una deriva verso ovest, di circa 0,32° all’anno (la differenza rispetto alla velocità di deriva del campo residuo non è significativa).

Le variazioni secolari sono state determinate direttamente da 200-300 anni; le caratteristiche fondamentali durante le ere geologiche si possono tuttavia dedurre dalla magnetizzazione delle rocce. Da questo studio è risultato che il campo magnetico terrestre ha subito in passato ripetute inversioni di polarità; inoltre, l’asse del dipolo centrale sembra aver cambiato notevolmente di direzione nell’intervallo di tempo che va dal periodo precambriano all’era terziaria: nell’ipotesi che l’asse del dipolo debba per ragioni fisiche discostarsi solo di poco dall’asse della rotazione terrestre, tale variazione manifesterebbe l’esistenza di una migrazione dei poli sulla crosta terrestre.

La causa delle variazioni secolari si ritiene strettamente connessa, come quella delle grandi anomalie regionali, al complesso dei fenomeni che sono all’origine del campo magnetico terrestre. In Italia, la variazione secolare della componente orizzontale è attualmente di circa +20 γ per anno; quella della declinazione è di circa 5′ per anno verso E. Le variazioni secolari si possono dedurre in modo attendibile solo dopo anni di misure, nascoste come sono da variazioni ben più rapide e vistose: la variazione regolare diurna e le variazioni irregolari sporadiche, o perturbazioni, che nei casi più cospicui prendono il nome di tempeste magnetiche.

3.2 Variazione diurna. - La variazione diurna è così chiamata perché per ciascuna componente essa si ripete ogni giorno, approssimativamente nello stesso modo. La sua ampiezza è dell’ordine di qualche decina di gamma, e le sue caratteristiche principali sono: a) essa procede secondo il tempo locale, presentando la massima intensità durante le ore meridiane, e affievolendosi fino a scomparire durante la notte; b) presenta un marcato effetto stagionale, essendo notevolmente più intensa d’estate che d’inverno; c) varia di intensità parallelamente al ciclo dell’attività solare; d) varia per ogni componente con la latitudine, sia in ampiezza sia in fase. Una particolarità importante è costituita dalla notevolissima ampiezza (fino a 200 γ) che la variazione della componente orizzontale presenta in una stretta fascia di latitudine lungo l’equatore magnetico.

La spiegazione della variazione diurna è data dalla cosiddetta teoria dinamo, proposta inizialmente da B. Stewart nel 1882 e successivamente perfezionata soprattutto da A. Schuster, S. Chapman, W.G. Baker e D.F. Martyn, e ora universalmente accettata. Secondo questa teoria, i moti regolari delle regioni ionosferiche, dovuti alle maree atmosferiche e alle differenze di densità e di pressione fra l’emisfero esposto al Sole e l’emisfero notturno, producono, a causa del campo magnetico terrestre, delle correnti indotte nella regione E della ionosfera, che a loro volta producono variazioni magnetiche al suolo; l’aumento della conducibilità ionosferica durante le ore meridiane, la stagione estiva e la fase di massima attività solare, dovuto alle radiazioni ultraviolette e X emesse dal Sole, spiega le caratteristiche fondamentali della variazione diurna. La teoria riesce anche a spiegare la grande ampiezza della variazione della componente orizzontale all’equatore magnetico, come dovuta a una corrente elettrica concentrata in direzione O-E all’altezza di 100-120 km, il cosiddetto elettrogetto equatoriale; l’esistenza di tale corrente è stata confermata da osservazioni dirette effettuate mediante razzi.

Oltre alla variazione diurna, che ha un periodo di 24 ore, è stata individuata una variazione lunare del campo magnetico, assai più piccola, che ha un periodo di 24h 50m (l’intervallo di tempo fra due passaggi successivi della Luna sullo stesso meridiano).

3.3 Tempeste magnetiche. - Le tempeste magnetiche sono variazioni sporadiche, di durata variabile da qualche ora a qualche giorno, caratterizzate da un’intensa agitazione, apparentemente disordinata, di tutti gli elementi del campo magnetico terrestre. In questo apparente disordine, tuttavia, si riconosce spesso un andamento caratteristico; la componente orizzontale presenta all’inizio un aumento (fase iniziale della tempesta) e successivamente una forte diminuzione (fase principale). Spesso le tempeste hanno inizio bruscamente, con un salto di qualche decina di gamma in pochi minuti.

L’intensità delle tempeste può variare da qualche decina a qualche migliaio di gamma. In questa variabilità ha un ruolo molto importante la latitudine; infatti all’aumentare di essa aumenta anche l’intensità delle fluttuazioni disordinate, fino a raggiungere un massimo in una fascia di latitudine attorno a 65°-70°, sia nell’emisfero Nord sia in quello Sud. Tale fascia coincide con la zona aurorale; in essa l’attività magnetica è non solo più intensa, ma anche più frequente che a latitudini inferiori, e ogni manifestazione di attività di una certa intensità è qui accompagnata da una manifestazione aurorale. Le tempeste magnetiche sono prodotte da nuvole di plasma di alta velocità espulse da certe regioni solari, soprattutto durante intensi brillamenti. Queste nuvole comprimono dinanzi a loro il plasma più lento emesso ordinariamente dal Sole (il cosiddetto vento solare quieto). Se la differenza di velocità fra i due plasmi supera (come spesso accade) la velocità del suono, si sviluppa un’onda d’urto, che si propaga nello spazio a velocità dell’ordine di 1000-2000 km/s, raggiungendo la Terra in circa due giorni (➔ anche vento). Qui essa interagisce col campo magnetico terrestre dando luogo a fenomeni complessi (tempeste magnetiche, aurore polari). Tempeste magnetiche hanno luogo anche negli anni in cui l’attività solare tende verso il minimo e non si producono brillamenti importanti; le perturbazioni magnetiche di queste epoche presentano in generale una tendenza a ripetersi ogni 27 giorni. Tenendo conto che questo intervallo di tempo corrisponde al periodo della rotazione sinodica del Sole, si conclude che in tali casi le nuvole di plasma vengono emesse con continuità da particolari regioni solari. Queste zone, un tempo chiamate regioni M, sono state identificate con i buchi coronali.

3.4 Baie. - Anche in assenza di vere e proprie tempeste magnetiche, si verificano spesso delle perturbazioni costituite da un rapido aumento (o rapida diminuzione) degli elementi magnetici, seguito da un ritorno altrettanto rapido al valore normale. Dall’aspetto che tali perturbazioni presentano sulle registrazioni fornite dai variografi, simile ai golfi quali appaiono sulle carte geografiche, a tali eventi si dà il nome di baie. La durata delle baie è generalmente di una o due ore, mentre la loro ampiezza, dell’ordine di qualche decina di gamma alle basse e medie latitudini, va crescendo fino a un massimo di varie centinaia di gamma nelle zone aurorali. Le baie sono attribuite a correnti elettriche concentrate, scorrenti a circa 100-150 km di altezza nella ionosfera della zona aurorale (elettrogetti aurorali).

3.5 Micropulsazioni e pulsazioni giganti. - Un altro tipo di variazioni magnetiche, assai meno intense delle precedenti ma ugualmente di notevole interesse, è costituito dalle micropulsazioni. Si tratta di oscillazioni del campo magnetico, di periodo compreso tra frazioni di secondo e qualche minuto e di intensità da frazioni di gamma ad alcuni gamma. Il fenomeno è morfologicamente alquanto complesso. In via generale si possono distinguere due classi di micropulsazioni: i treni di pulsazioni, indicati con il simbolo pi, e le pulsazioni continue, indicate con il simbolo pc. Le prime si presentano sotto forma di treni d’onde, spesso smorzati, della durata media di qualche decina di minuti, con periodo di circa 50-1200 s e ampiezza da 0,5 γ ad alcuni gamma; esse si verificano prevalentemente nelle ore notturne e sono molto spesso associate con l’inizio delle baie. I treni d’onda sono registrati contemporaneamente su di una vasta estensione della Terra, talora su tutto il pianeta. Le pulsazioni pc sono costituite da onde più regolari delle precedenti, spesso sotto forma di oscillazioni sinusoidali di periodo, in generale, di circa 10-60 s e aventi ampiezza 0,1-1 γ; la loro durata si estende non di rado a parecchie ore, ed esse si presentano prevalentemente durante le ore diurne.

Oltre alle pulsazioni dei due tipi ora ricordati esistono anche le cosiddette pulsazioni giganti (pg), costituite da oscillazioni regolari aventi un periodo di alcuni minuti e ampiezza fino a qualche decina di gamma: si tratta di eventi non molto frequenti ed estremamente localizzati, soprattutto alle latitudini aurorali. Le micropulsazioni vengono in generale spiegate come effetto di onde magnetoidrodinamiche nella magnetosfera.

4. Origine del campo magnetico terrestre

La concezione di un campo magnetico terrestre principale che si origina nel nucleo fluido della Terra, tra circa 2900 e 5200 km di profondità, dà luogo alla trattazione della problematica dell’origine del campo magnetico terrestre in termini di ‘origine del campo nucleare’. Gli studi sul campo principale sono orientati alla comprensione del suo meccanismo di generazione e sostentamento nell’ambito di un’impostazione magnetofluidodinamica, ovvero della dinamica del plasma fluido del nucleo esterno della Terra soggetto alle complesse interazioni con la rotazione terrestre e i campi terrestri. Si tratta di risolvere le equazioni di Maxwell dell’elettromagnetismo e l’equazione di Navier-Stokes della fluidodinamica, che forniscono la prima e la seconda equazione della magnetofluidodinamica per il plasma del nucleo terrestre; tale impresa presenta cospicue difficoltà di calcolo, che non sono state ancora completamente risolte.

Soluzioni di tipo euristico, ottenute mediante opportune semplificazioni, mostrano che a seguito dei moti, reciprocamente ortogonali, di rotazione e di convezione, nel nucleo si destano correnti di plasma di tipo circolare; se inizialmente nel nucleo è presente un campo magnetico, anche di debole intensità, che abbia una componente non nulla secondo l’asse della rotazione terrestre, le correnti di plasma sono risolte in un sistema di correnti elettriche elicoidali tali che il campo magnetico da esse generato rinforzi il campo iniziale, fino al raggiungimento di una situazione di equilibrio tra le energie attive e passive in gioco, cui corrisponde la costanza del campo magnetico.

Gli studi sulla risoluzione incondizionata delle equazioni della magnetofluidodinamica nell’ambito geomagnetico sono volti essenzialmente a dare conto, facendo alcune ipotesi sulla non omogeneità elettromagnetica del nucleo terrestre, delle irregolarità sia temporali sia geografiche del campo magnetico terrestre messe in evidenza dalle misurazioni; in particolare, sembra che le inversioni e la deriva occidentale possano essere soddisfacentemente spiegate con l’ipotesi della formazione di onde magnetofluidodinamiche di grandissimo periodo e piccola velocità nel nucleo terrestre.

In effetti, si ritiene che la parte esterna del nucleo terrestre possa essere formata da un fluido di bassa viscosità, costituito da un plasma molto caldo e molto denso, con temperatura fra 2700 e 3200 K, pressione fra 1 e 3,5∙10¹¹ Pa (cioè fra 1 e 3,5 milioni di volte la pressione atmosferica al suolo) e, a motivo dell’alta temperatura, con permeabilità magnetica che può essere assunta pari a quella del vuoto, M_o; tale plasma, composto essenzialmente di ferro fuso con piccole percentuali di altri elementi, sarebbe sottoposto a un vigoroso moto convettivo, generante flussi di materia con velocità medie dell’ordine di 10 km/anno. Questa convezione è dovuta al rimescolamento generato dalla discesa degli elementi più pesanti della miscela (sostanzialmente ferro) verso la base, al confine con il nucleo solido, e dalla tendenza al galleggiamento degli elementi più leggeri, che risalgono invece verso il mantello.

Oltre al citato moto, è presente anche una convezione termica dovuta al fatto che il nucleo solido della Terra, più interno, accrescendosi rilascia calore latente di solidificazione, che riscalda il nucleo fluido e contribuisce alla convezione. Si ritiene che tra i due meccanismi quello di tipo composizionale-gravitativo sia prevalente e che la convezione termica contribuisca solo limitatamente ai moti nel nucleo fluido. La cinematica di questo moto è vincolata alla rotazione terrestre, che fa assumere al fluido una disposizione geometrica con ‘tubi di flusso convettivi’ paralleli all’asse di rotazione terrestre.

Dalle informazioni provenienti da studi paleomagnetici, che forniscono direzione e intensità del campo magnetico terrestre nelle epoche geologiche, è noto che il campo magnetico terrestre ha invertito la sua polarità in maniera non regolare numerose volte nella storia della Terra. Due aspetti di questo fenomeno sono ora evidenti. In primo luogo si è osservata una graduale variazione nella frequenza media di occorrenza delle inversioni: infatti, nelle ultime decine di milioni di anni il fenomeno è divenuto molto più frequente che in passato; in secondo luogo si è notato che, durante la transizione che porta alla migrazione dei poli magnetici da un emisfero all’altro, il percorso dei poli mostra, in questo intervallo di tempo, allineamenti statisticamente persistenti nelle stesse aree geografiche. Tale persistenza viene interpretata come indicazione di un’influenza sulla dinamica del nucleo e quindi sulla geodinamo, che agisce dall’esterno. Si ritiene infatti che la generazione del campo magnetico terrestre sia condizionata dalla presenza di eterogeneità laterali alla base del mantello, anche se non è ancora chiaro come il mantello eserciti questa sua influenza sul nucleo. I meccanismi che sono stati proposti per questo accoppiamento sono di tre tipi: di tipo termico, che metterebbe in relazione la convezione del mantello con quella del nucleo; di tipo meccanico, dovuto a una topografia variabile alla base del mantello; di tipo elettromagnetico, per mezzo delle variazioni di conducibilità elettrica alla base del mantello che comporterebbero una dispersione delle correnti elettriche dal nucleo fluido al mantello. Tutti questi tipi di meccanismi potrebbero causare deflessioni del flusso di materia alla superficie del nucleo fluido, modificando quindi il meccanismo della dinamo.

Il campo magnetico terrestre non si estende indefinitivamente nello spazio, come avverrebbe se la Terra si trovasse nel vuoto. Infatti, il vento solare, un flusso di plasma magnetizzato proveniente dal Sole, lo confina a una regione circostante la Terra, detta cavità geomagnetica o magnetosfera.

5. Descrizione del campo magnetico terrestre

Il tradizionale modello gaussiano del dipolo centrale come sorgente è usato soltanto per considerazioni di primissima approssimazione e di tipo naturalistico, mentre per rappresentare il campo magnetico terrestre nel suo insieme si usano esclusivamente modelli numerici, costituiti da tabelle dei valori dei coefficienti g^m_n e h^m_n di Gauss (coefficienti risultanti dall’analisi in armoniche sferiche del campo magnetico medio) e delle loro derivate temporali prime rispetto a un dato periodo di tempo (di norma, 12 mesi), arrestati a un certo grado. La IAGA (International Association of Geomagnetism and Aeronomy), che si occupa, oltre che dell’aeronomia, in primo luogo del coordinamento e della normazione delle ricerche sul campo magnetico terrestre, pubblica con cadenza quinquennale, a partire dai dati rilevati dalla rete mondiale di osservatori magnetici, un modello numerico di questo tipo fino al grado 10 per i coefficienti e per le loro derivate temporali prime, modello chiamato International geomagnetic reference field e indicato abitualmente con la sigla IGRF, seguita dall’epoca di validità.

astronomia

M. planetario Le sonde spaziali hanno ricercato la presenza di campi magnetici su tutti i pianeti del Sistema solare, eccetto Plutone. Fra i pianeti interni, è risultato che solo Mercurio (a parte, s’intende, la Terra) possiede sicuramente un campo magnetico di origine endogena. Si tratta, tuttavia, di un campo assai debole, corrispondente a un dipolo il cui momento è ∿4∙10–4 MT (dove MT = 8∙1025 u.e.m. è il momento del dipolo terrestre). È possibile che Marte abbia un campo magnetico avente un’intensità superficiale corrispondente a un dipolo di momento ∿10–4 MT. Nessun campo magnetico è stato misurato su Venere: se il pianeta ne ha uno, il momento magnetico del suo dipolo sarebbe inferiore a 5∙10–5 MT. Assai più intensi sono i campi magnetici dei pianeti esterni. L’esistenza del campo di Giove fu stabilita ancor prima che esso venisse raggiunto dalle sonde spaziali: si era infatti trovato che il pianeta è una intensa sorgente di onde radio e tale emissione (più precisamente quella alle lunghezze d’onda decimetriche) era stata interpretata come radiazione di sincrotrone prodotta da elettroni energetici intrappolati in un campo magnetico. Le osservazioni dirette delle sonde Pioneer X e XI e Voyager I e II hanno confermato che Giove possiede una fascia di radiazione simile e assai più estesa della cintura di Van Allen della Terra. È risultato anche che il campo magnetico superficiale, all’equatore, ha un’intensità di ∿4 oersted. Tenendo conto delle dimensioni del pianeta, questo campo corrisponde a un dipolo centrale avente un momento pari a ∿2∙104 MT. Saturno ha un campo magnetico meno intenso di quello di Giove: il momento del suo dipolo è ∿550 MT. L’asse del dipolo coincide quasi esattamente con l’asse di rotazione ed è diretto nello stesso senso di questo. Le misure dei campi magnetici di Urano e di Nettuno sono state effettuate da Voyager I, che ha incontrato i due pianeti rispettivamente nel 1986 e nel 1989. La caratteristica più singolare dei campi magnetici di entrambi i pianeti è che essi derivano da dipoli i cui assi sono molto inclinati rispetto ai rispettivi assi di rotazione.

La Luna, che è il satellite meglio studiato, è priva, attualmente, di un campo magnetico apprezzabile: tuttavia, l’analisi dei campioni di rocce, raccolti nelle missioni Apollo, ha mostrato che essa potrebbe averne posseduto uno molto debole nel passato.

Quanto all’origine dei campi magnetici planetari, sarebbero generati, come il campo della Terra, attraverso un meccanismo simile a quello di una dinamo autoeccitata; le osservazioni compiute dalle sonde spaziali hanno costituito un prezioso banco di prova per tale teoria. Affinché possano generarsi campi magnetici col meccanismo della dinamo, occorre che un pianeta: a) sia costituito, tutto o in parte, da un fluido conduttore rimescolato da correnti convettive; b) sia animato da un moto di rotazione abbastanza rapido. Ci si aspetta, pertanto, che solo i pianeti che soddisfano entrambe queste condizioni siano dotati di un campo magnetico. La teoria dinamo prevede, inoltre, che l’asse del dipolo magnetico di un pianeta sia approssimativamente (ma non esattamente) allineato col suo asse di rotazione; per quanto riguarda il verso, invece, il dipolo può essere orientato indifferentemente in un senso o nell’altro. Le osservazioni hanno confermato solo parzialmente tali aspettative. Per es., l’assenza di un campo magnetico apprezzabile su Venere è in accordo con la teoria: questo pianeta, infatti, pur possedendo probabilmente un nucleo metallico liquido, ha una velocità di rotazione troppo lenta (il periodo di rotazione è di 243 giorni) per poter sostenere una dinamo. Sorprendente è stata, invece, la scoperta di un campo magnetico su Mercurio. Questo pianeta deve possedere un esteso nucleo metallico (come indicato dall’elevato valore della sua densità media di 5,4 g/cm³), tuttavia, data la piccola massa del pianeta, ci si aspettava che questo nucleo fosse interamente solido; inoltre, il moto di rotazione sembrerebbe troppo lento (il periodo è di circa 59 giorni) per potere alimentare una dinamo. Passando ai pianeti esterni, si nota, innanzi tutto, che i loro campi magnetici si discostano dall’andamento di dipolo assai più di quello della Terra: ciò suggerisce che le sorgenti del campo siano distribuite su larga parte del pianeta piuttosto che essere concentrate nel suo nucleo. Si pensa che in Giove e Saturno il fluido conduttore, nel quale circolano le correnti elettriche che generano il campo magnetico, sia rappresentato da idrogeno metallico liquido, cioè idrogeno ionizzato allo stato liquido.