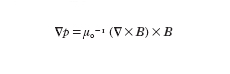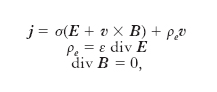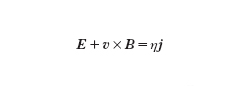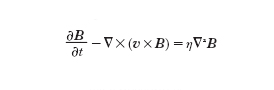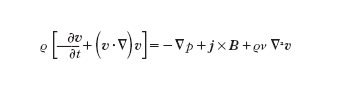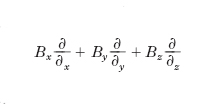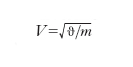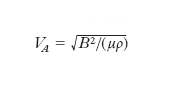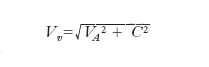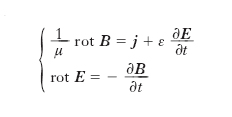magnetofluidodinamica

Teoria del moto di un fluido elettricamente conduttore in presenza di un campo magnetico, indicata correntemente con la sigla MHD (magnetohydrodynamics). Le correnti elettriche indotte nel fluido per effetto del moto modificano il campo, mentre per la presenza di questo si determinano forze che influiscono variamente sul moto stesso. Questa mutua azione fa insorgere fenomeni, detti magnetofluidodinamici, non contemplati nell’elettromagnetismo o nella fluidodinamica. La teoria è detta anche magnetoidrodinamica o idromagnetismo nel caso di un liquido, magnetogasdinamica nel caso di un fluido compressibile, magnetoplasmadinamica nel caso di un plasma.

I fenomeni magnetofluidodinamici svolgono un ruolo fondamentale nel cosmo. Poiché le stelle consistono in gran parte di materia ionizzata, quindi elettricamente conduttrice, la m. regola molti dei processi che vi avvengono. La m. è anche importante per lo studio della radiazione cosmica, della ionosfera e della magnetosfera terrestre (e dei fenomeni a questa connessi come le aurore polari e le tempeste geomagnetiche).

Equazioni fondamentali

Le equazioni che reggono i fenomeni della m., considerati sotto l’aspetto continuo, si ottengono associando, con le opportune modifiche imposte dalla mutua azione, le equazioni dell’elettromagnetismo a quelle della fluidodinamica. Precisamente, siano E l’intensità del campo elettrico, B l’induzione magnetica, v la velocità delle particelle del mezzo, j la densità della corrente elettrica di conduzione, μ la permeabilità magnetica assoluta, ε la costante dielettrica assoluta, σ la conduttività elettrica, ρ_e la densità volumica di carica elettrica, p la pressione, ρ la densità, η la viscosità dinamica, F il risultante delle forze di tipo non elettromagnetico applicate all’unità di massa (dovute alla gravitazione ecc.), se il mezzo è omogeneo e isotropo e se si adotta per le unità di misura il Sistema internazionale, si ha:

[1] formula;

,

e

[2] formula.

Le [1] sono le equazioni di Maxwell. Le [2] (➔ idrodinamica) sono nell’ordine: l’equazione del moto di un fluido viscoso, modificata per l’aggiunta dei termini elettromagnetici; l’equazione di continuità, che esprime la legge di conservazione della massa; l’equazione di stato (f=0), assunta, per semplicità, come una relazione fra la densità e la pressione (in questa forma semplificata, essa è valida in molti casi di interesse pratico: per es., in quello di un gas perfetto in condizioni isoterme o adiabatiche). Le [1] e [2] equivalgono a un complesso di 11 equazioni scalari in altrettante incognite scalari (p, ρ, le tre componenti di E, quelle di B, quelle di v). È da notare che i termini di mutua azione sono tutti non lineari: in [1] si hanno infatti, per effetto del moto, i termini v×B e ρ_ev, il primo dovuto all’azione del campo magnetico sulle cariche di conduzione in movimento e il secondo interpretabile come densità di corrente elettrica di convezione; in [2], per la presenza del campo elettromagnetico, si hanno i termini j×B, forza di Lorentz esercitata sull’unità di volume per azione dell’induzione B sulla corrente di densità j, e ρ_eE, forza esercitata dal campo elettrico E sulla carica ρ_e esistente nell’unità di volume. Il problema matematico è, in generale, per la presenza di termini di mutua azione non lineari, di estrema difficoltà.

Effetti elettromagnetici: diffusione e congelamento del campo magnetico

Le equazioni [1] possono essere combinate fra loro, eliminando il campo elettrico E. Si ottiene così l’equazione dell’induzione magnetica:

[3] formula.

La [3] ha due casi limite notevoli: a) se il fluido è in quiete (v = 0), il primo termine a secondo membro si annulla e la [3] si riduce alla equazione di diffusione. Si trova allora che un campo magnetico, inizialmente localizzato in un punto, si dif;fonde a tutto il fluido in un tempo (detto tempo di diffusione del campo magnetico) τ=μσL², dove L è una dimensione caratteristica del fluido. b) Se il fluido è perfettamente conduttore (σ=∞), il secondo termine a secondo membro si annulla e la [3] si riduce alla equazione del congelamento del campo magnetico (➔ congelamento). In questo caso, il campo magnetico è ‘congelato’ nel fluido, cioè le sue linee di forza sono ‘incollate’ alle particelle e si muovono insieme a queste (teorema di Alfvén). In pratica, per stabilire qual è il comportamento di un fluido, si considera il suo numero di Reynolds magnetico (R_m=Lvμσ), che esprime il rapporto (in ordine di grandezza) fra il primo e il secondo termine a secondo membro della [3]: se R_m ≪1 prevale la diffusione; se R_m≫1 prevale il congelamento. Questa seconda situazione (detta limite di conduttività infinita) si verifica spesso nei plasmi cosmici non tanto perché la conduttività elettrica sia effettivamente tanto elevata, ma piuttosto per le enormi dimensioni dei sistemi con cui si ha a che fare (infatti, per L→∞, R_m→∞). Notiamo che nel limite di conduttività infinita (σ=∞), il campo elettrico deve essere E=−v×B per mantenere finita la densità della corrente elettrica j=σ (E+v×B). In quanto segue, salvo diverso avviso, supporremo sempre di trovarci in questa situazione.

Pressione e tensione magnetiche

Nella [2], la forza di Lorentz (j×B), che agisce sulla unità di volume di fluido, può essere espressa come segue:

[4] formula,

dove B∙grad indica l’operatore

Il primo termine a secondo membro descrive una forza di pressione (infatti, esso ha la stessa forma del termine −grad p, che esprime la forza di pressione termica che agisce sull’unità di volume di fluido). Si definisce pertanto una pressione magnetica (B²/2μ), che ha sul fluido effetti del tutto analoghi a quelli della pressione termica. Il secondo termine descrive, invece, una forza di tensione, analoga a quella che agisce in una corda elastica tesa. Le linee di forza del campo magnetico si comportano pertanto come corde elastiche: se vengono incurvate, allungandole, esse tendono a contrarsi ritornando rettilinee. La tensione magnetica, che agisce su un tubo di forza di sezione unitaria, è B²/μ.

Onde magnetoidrodinamiche (onde MHD)

Il fatto che le linee di forza, in un fluido perfettamente conduttore, si comportino come corde elastiche, condusse H. Alfvén, nel 1942, a scoprire le onde MHD, che portano il suo nome. Pizzicando una corda elastica, si generano in essa onde trasversali che si propagano con la velocità

,

dove ϑ è la tensione della corda e m la sua massa specifica lineare. Ci si aspetta allora che, perturbando una linea di forza magnetica, questa cominci a vibrare insieme alle particelle del fluido che sono ‘incollate’ a essa. La velocità delle onde (trasversali) così generate deve essere

,

dove B²/μ è la tensione magnetica e ρ la massa specifica del fluido (che può essere interpretata come massa specifica lineare, se si considera un tubo di forza di sezione unitaria). La velocità V_A viene chiamata velocità di Alfvén. La trattazione matematica delle onde di Alfvén si basa sulle equazioni [2] e [3]; si possono avere due casi: a) fluido incomprimibile (liquido) e b) fluido comprimibile (aeriforme). Nel fluido incomprimibile, ponendo B=B₀+b, dove B₀ rappresenta una intensa induzione magnetica uniforme presente nel fluido e b una perturbazione sufficientemente piccola, da poter trascurare nelle equazioni i termini quadratici in b e in v in confronto ai termini lineari, si trova che nel fluido la perturbazione, rappresentata da b e da v, si propaga quindi sotto forma di onde piane (progressive e retrograde), con la velocità di Alfvén V_A, nella direzione delle linee di forza del campo magnetico. I vettori b e v sono paralleli fra loro e perpendicolari a B₀ e, quindi, anche alla direzione di propagazione delle onde (le onde, cioè, sono trasversali). La presenza della viscosità o della resistività elettrica del fluido ha l’effetto di provocare il progressivo smorzamento delle onde. Per onde di lunghezza d’onda λ, si trova che il tempo di smorzamento è dell’ordine di λ²/ν (dove ν è la viscosità cinematica) nel primo caso e di μσλ² nel secondo.

Le onde di Alfvén sono le uniche onde MHD che possano generarsi in un fluido incomprimibile. In un fluido comprimibile esistono, invece, altri due tipi di onde MHD, che, a differenza delle onde di Alfvén, sono compressive. La trattazione matematica di queste onde (dette onde magnetosoniche) è assai complessa, tuttavia è possibile comprenderne l’origine senza ricorrere al formalismo matematico. Le onde del primo tipo (onde magnetosoniche lente) sono analoghe alle onde acustiche che si sviluppano in un aeriforme non magnetizzato. Nella direzione delle linee di forza, queste onde si riducono proprio a onde acustiche, in quanto la loro propagazione non è perturbata dal campo magnetico (infatti, la forza di Lorentz si annulla se le particelle oscillano parallelamente a B, come avviene per un’onda acustica che si propaghi in tale direzione). Nelle altre direzioni si risentono gli effetti della forza di Lorentz, sicché le onde risultano modificate rispetto alle onde acustiche ordinarie. Le onde del secondo tipo (onde magnetosoniche veloci) sono più strettamente legate alla presenza del campo magnetico. Esse sono generate dalla pressione magnetica allo stesso modo in cui, in un fluido ordinario, la pressione termica genera le onde acustiche. Sia le onde magnetosoniche lente sia quelle veloci hanno velocità diverse a seconda della direzione in cui si propagano: la presenza del campo magnetico introduce, dunque, un’anisotropia nel mezzo. D’altra parte, qualunque sia la direzione considerata, l’onda magnetosonica lenta ha una velocità minore dell’onda magnetosonica veloce. In particolare, nella direzione perpendicolare alle linee di forza del campo magnetico, la velocità dell’onda lenta si annulla (V_l=0), mentre quella dell’onda veloce raggiunge il valore massimo

,

dove C è la velocità del suono nel mezzo).

Altri fenomeni magnetofluidodinamici

Esistono molti altri fenomeni magnetofluidodinamici, che sono stati oggetto di studio sia per il loro interesse cosmico sia per quello legato ad applicazioni tecnologiche. Uno dei problemi più importanti è quello della stabilità di una configurazione, statica o dinamica, di un fluido conduttore magnetizzato. In generale, si ha stabilità, se qualsiasi piccola perturbazione tende a smorzarsi nel tempo; instabilità se, invece, vi è qualche tipo di perturbazione che, una volta generata, tende ad accentuarsi, distruggendo (o alterando) così la configurazione iniziale del fluido. L’analisi delle instabilità MHD è quanto mai complessa. Un esempio è fornito dai tentativi di realizzare la fusione nucleare controllata (➔ fusione; ➔ reattore), confinando un plasma con campi magnetici. I problemi teorici sull’equilibrio del fluido sono complessi e non è nota (e forse non esiste) alcuna soluzione rigorosa delle equazioni che regolano il fenomeno in spazi privi di qualsiasi simmetria. Si è proceduto a sperimentazioni di confinamento magnetico in dispositivi con simmetrie di traslazione e/o di rivoluzione, o in casi per i quali si conoscono soluzioni approssimate che garantiscono l’equilibrio del fluido entro un grado di precisione sufficiente per gli scopi sperimentali. In questi casi, si è dimostrato possibile evitare lo sviluppo di instabilità macroscopiche e mantenere un plasma confinato per tempi molto più lunghi di quelli caratteristici delle instabilità MHD.

Generatori magnetofluidodinamici

Si tratta di dispositivi, in fase di studio, che realizzano la conversione diretta dell’energia termica in energia elettrica. Sono stati anche sviluppati progetti dettagliati di impianti industriali da 1000 MW elettrici, ma dopo intensi studi nel periodo 1960-1980, l’interesse si è attenuato in conseguenza di permanenti gravi difficoltà tecnologiche. Inoltre, i progressi nello sviluppo delle turbine a gas e degli impianti con cicli combinati gas-vapore dai rendimenti sempre più elevati hanno ridotto il potenziale vantaggio della conversione diretta.

fig.

I generatori magnetofluidodinamici sono costituiti in linea schematica (v. fig.) da un condotto divergente, di materiale ceramico, con una serie di coppie di elettrodi metallici contrapposti. Un elevato campo di induzione magnetica B, uniforme e costante, diretto perpendicolarmente all’asse del condotto, è generato da un elettromagnete. I gas ad altissima temperatura prodotti in una camera di combustione vengono accelerati attraverso un ugello e quindi fatti fluire nel condotto con velocità v. È sufficiente una parziale ionizzazione del gas per indurre in esso una forza elettromotrice E, rilevabile tra gli elettrodi, analoga a quella che si produrrebbe in un conduttore metallico in moto alla stessa velocità v nel campo di induzione magnetica B. Con il passaggio della corrente di carico si determinano azioni sugli ioni e sugli elettroni del fluido che stabiliscono una differenza di pressione tra l’ingresso e l’uscita del condotto, e quindi determinano la quantità di potenza convertita direttamente in potenza elettrica.