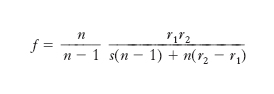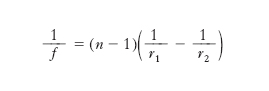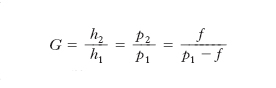lente
Fisica
In ottica, in generale, si chiama l. (o meglio, l. semplice) il sistema ottico centrato costituito da 2 diottri rifrangenti adiacenti, ambedue curvi oppure uno curvo e l’altro piano, cioè il sistema costituito da una porzione di materiale trasparente omogeneo, limitato da 2 superfici S1, S2, una almeno delle quali sia curva. L’asse principale ottico (o asse ottico) della l., è la retta congiungente i centri di curvatura delle due superfici; se una di queste è piana, l’asse è la normale alla superficie piana condotta per il centro di curvatura della superficie curva.
Cenni storici
Circa la scoperta delle l. non si hanno indicazioni certe. Peraltro l’impiego di l. d’ingrandimento e di l. ustorie deve risalire a tempi molto antichi, come si rileva da passi di classici (Aristofane, Plinio ecc.) e come provano alcuni ritrovamenti di l. in tombe romane e l’esistenza di lavori di tale finezza da ritenere impossibile la loro esecuzione senza l’ausilio di l. d’ingrandimento.
L. sferiche
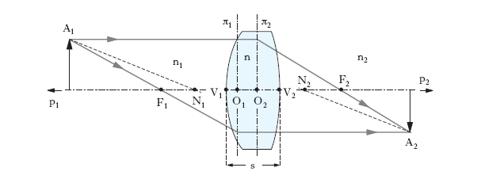
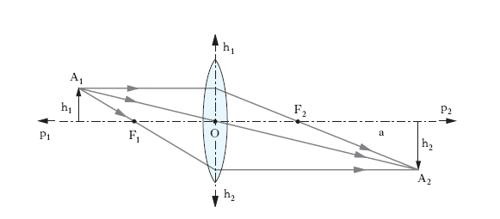
Le l. di gran lunga più importanti sono quelle sferiche, limitate cioè da superfici sferiche; data la simmetria rispetto all’asse ottico, tutte le considerazioni geometriche relative al cammino dei raggi possono farsi per tali l. considerando un qualunque piano per l’asse medesimo. La teoria delle l. sferiche, cioè la determinazione delle relazioni che consentono di precisare la posizione e la forma delle immagini ove si conoscano le caratteristiche delle l. e dei mezzi ottici nonché la forma e la posizione degli oggetti, derivano direttamente dalla teoria generale dei sistemi ottici centrati. Le caratteristiche da conoscere sono i raggi di curvatura r1 della faccia su cui incide la luce e r2 della faccia dalla quale emerge la luce rifratta, e gli indici di rifrazione assoluti del materiale di cui è formata la l., n, e dei mezzi che si trovano da una parte e dall’altra della l., n1 e n2. Se ci si pone nell’approssimazione di Gauss, cioè se si considerano raggi poco inclinati sull’asse e incidenti sulla l. a piccola distanza dai vertici V1 e V2 (fig. 1) della l. medesima, dalle formule che in tale approssimazione si possono scrivere per i 2 diottri è possibile ricavare la posizione dei 6 punti cardinali, e cioè la posizione dei 2 punti principali, O1, e O2 (e quindi dei 2 piani principali π1 e π2), dei due punti focali, o fuochi, F1 e F2, e dei due punti nodali, o nodi, N1 e N2 (➔ sistema). Si hanno così tutti gli elementi per determinare la posizione delle immagini, infatti: a) i punti coniugati sui piani principali si corrispondono in posizione, cioè sono congiunti da segmenti paralleli all’asse ottico; b) i fuochi sono i coniugati dei punti all’infinito dell’asse, cioè per essi passano i raggi coniugati di raggi paralleli all’asse; c) i raggi coniugati per i nodi sono paralleli tra loro. Per determinare graficamente il punto coniugato A2 di un punto A1 basta considerare, come indicato nella fig. 1, il cammino fittizio del raggio per A1 parallelo all’asse (rifratto quindi nel secondo fuoco, F2) e del raggio per A1 passante per il primo fuoco (rifratto quindi, parallelamente all’asse). Le formule che, nel caso generale finora considerato, danno le ascisse dei fuochi in funzione degli indici di rifrazione dei mezzi e dei raggi di curvatura della l. sono abbastanza complesse. Esse si semplificano notevolmente se il mezzo al di qua e al di là della l. è lo stesso, generalmente l’aria. Le distanze dei fuochi dai punti principali (O1F1 e O2F2 in fig. 1) divengono allora uguali: nodi e punti principali coincidono; la l. è caratterizzata da una sola distanza focale, il valore f delle ascisse dei fuochi, valutate, come ogni altra lunghezza, riferendo lo spazio-oggetti e lo spazio-immagini ai due assi p1 e p2, aventi uno l’origine in O1, l’altro in O2, e orientati come mostra la figura. In particolare, detto s lo spessore della l. e n l’indice di rifrazione del materiale della l. relativamente al mezzo in cui la l. è immersa, si ha per la distanza focale:
(1) formula
I raggi di curvatura, r1 e r2, che compaiono in queste relazioni sono assunti positivi oppure negativi a seconda che la superficie cui si riferiscono volga la convessità oppure la concavità verso la direzione dalla quale si immagina provenga la luce. Così, per la l. biconvessa della fig. 1, se si assume lo spazio in cui si trova il punto A1 come spazio-oggetti (donde dunque proviene la luce), r1 è positivo, r2 è negativo, ed è r1r2<0. Se, come ordinariamente accade, è n>1 (per es., l. di vetro immersa in aria), f risulta positiva oppure negativa a seconda che r1+ ∣r2∣ sia maggiore oppure minore di s(n−1)/n; il contrario accade se è n<1 (per es., l. di vetro immersa in solfuro di carbonio, che è più rifrangente del vetro); il segno di f non muta se si immagina che lo spazio-immagini divenga spazio-oggetti, e viceversa. Il riferimento alla distanza focale f è importante perché è in effetti tale grandezza che caratterizza completamente, con il suo valore e con il suo segno, una l.; in particolare, l’essere f positiva oppure negativa significa che la l. rifrange i raggi in modo da avvicinarli oppure in modo da allontanarli dall’asse ottico, cioè che la l. è convergente (f>0) oppure divergente (f<0). Considerazioni analoghe possono farsi nel caso di l. non biconvesse: biconcave, piano-convesse, concavo-convesse, o menischi ecc.
L. sottili
Si considera l. sottile una l. il cui spessore s sia trascurabile rispetto a ogni altra lunghezza che compare nel problema che si sta considerando (in particolare, rispetto ai raggi di curvatura). In tal caso i punti principali, e quindi anche i nodi, coincidono con i vertici che possono pensarsi coincidenti in uno stesso punto O, detto centro ottico della l. sottile: proprietà essenziale di tale punto (che è un punto nodale per così dire ‘doppio’) è che i raggi passanti per esso non subiscono alcuna deviazione. Dalla (1) si ricava per la convergenza, cioè per l’inverso della distanza focale, la relazione:
(2) formula
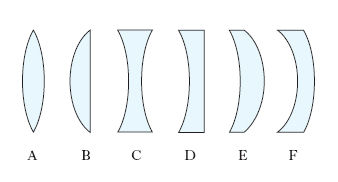
Per riconoscere rapidamente se una l. sottile è convergente o divergente basta semplicemente vedere se la l. in questione è più spessa al centro o ai bordi. Se, come ordinariamente accade, la l. è più rifrangente del mezzo in cui si trova, sono convergenti le l. più spesse al centro che ai bordi (in fig. 2, le l. A, B, E), e divergenti quelle più spesse ai bordi che al centro (in fig. 2, le l. C, D, F); si ha il contrario se, come talvolta succede, la l. è meno rifrangente del mezzo che la circonda. Questa semplice regola compendia i risultati che, per quanto riguarda il segno di f, si ricavano dalla (2) prendendo per r1 e r2 i loro valori algebrici. È possibile dimostrare che tra l’ascissa p1 dei punti-oggetto, valutata sull’asse ottico a partire dal centro O verso lo spazio-oggetti, e l’ascissa p2 dei punti-immagine, valutata sul medesimo asse, con la medesima origine ma in verso opposto al precedente, intercorre la relazione (formula delle l. sottili):
(3) formula
La (2) e la (3) consentono di determinare senza difficoltà l’ascissa p2 dell’immagine, noti che siano l’ascissa dell’oggetto, i raggi di curvatura della l. e l’indice di rifrazione della l. rispetto al mezzo circostante. Se p2 risulta positiva, l’immagine cade nello spazio-immagini, e per i punti di essa passano effettivamente i raggi rifratti della l. (immagine reale); se invece p2 risulta negativa, vuol dire che l’immagine è nello spazio-oggetti, cioè che per i punti di essa passano non i raggi rifratti, che in tale spazio non si propagano, ma i prolungamenti di essi (immagine virtuale).
Qualora, anziché una determinazione analitica, si voglia una determinazione grafica, si può ricorrere alla costruzione schematizzata nella fig. 3, in cui, analogamente alla fig. 1, si determina il punto immagine A2 come intersezione dei raggi rifratti corrispondenti a 2 dei seguenti 3 che escono dal punto oggetto A1: il raggio ‘parallelo’ all’asse; il raggio ‘centrale’; il raggio passante per il fuoco F1. La distanza dei punti, oggetto e immagine, dall’asse ottico a può essere valutata riferendosi a un asse, condotto per O normalmente ad a (fig. 3) e orientato in un certo verso per le distanze h1 dei punti-oggetto e nel verso opposto per le distanze h2 dei punti-immagine; dalla fig. 3 si ricava allora per l’ingrandimento lineare della l. il valore espresso dall’uno o l’altro dei rapporti seguenti:
(4) formula
Se è ∣G∣<1, l’immagine è impiccolita, mentre se è ∣G∣>1, l’immagine è ingrandita; se è G>0, l’immagine, come in fig. 3 è capovolta rispetto all’oggetto, mentre è diritta se è G<0. Come si riconosce dalle relazioni precedenti, una l. convergente dà immagini reali e capovolte di oggetti reali che distino da essa più della distanza focale f; tali immagini sono impiccolite se l’oggetto è al di là del doppio della distanza focale; ingrandite se la distanza p1 dell’oggetto è tra 2f e f (in particolare, per p1=2f è G=1, e per p1=f è G=∞); le immagini sono invece virtuali, diritte, ingrandite se l’oggetto è tra il fuoco e la l. (come nel caso della l. d’ingrandimento). Una l. divergente dà invece sempre immagini virtuali, diritte, impiccolite di oggetti reali. Tutto ciò è schematicamente mostrato nella fig. 4.
Tutto quanto detto finora vale nel caso, puramente teorico, che le approssimazioni di Gauss siano effettivamente soddisfatte e che la luce incidente sia monocromatica; in realtà, la formazione delle immagini è complicata dal cromatismo e dalle varie aberrazioni geometriche di cui, in misura più o meno pronunciata, una l. è inevitabilmente affetta.
L. di Fresnel
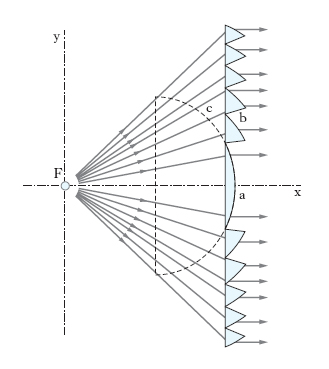
Dispositivo rifrangente costituito da una lente a (fig. 5) e da una serie di prismi, b, di forma opportuna, disposti tutt’intorno ad a, ed equivalente nel complesso a una l. di grande apertura relativa. Si può considerare tale l. derivata da una l. sferica (nel caso della fig. 5, una l. piano-convessa, di cui con c è indicato il profilo sferico) da cui vengano asportate zone di forma opportuna (di qui l’altra denominazione di l. a zone, o l. zonata), con conseguente notevole riduzione delle dimensioni e del peso. Inoltre la l. Fresnel rispetto a una l. ordinaria, per es. piano-convessa, di pari apertura relativa mostra minori perdite di luce per assorbimento. Le l. di Fresnel trovano applicazione in quasi tutti i fari marittimi e aeronautici, per autoveicoli, per segnalamento marittimo, ferroviario, stradale ecc.
Altri tipi di lenti
L. elettriche ed elettroniche
Nell’ottica delle onde hertziane, si chiama l. qualsiasi dispositivo atto a produrre fenomeni di rifrazione delle onde medesime, analoghi, per non dire identici, a quelli prodotti dalle l. ordinarie per la luce, e usati in particolare per far convergere onde su un ricettore o per trasformare in un fascio parallelo le onde sferiche emesse da un radiatore pressoché puntiforme.
In ottica elettronica, si chiama l. un dispositivo costituito da un certo numero di conduttori di forma opportuna, portati a differenti potenziali elettrostatici (l. elettrostatica), o di magneti (l. magnetica), o di conduttori e magneti (l. di tipo misto), capace di deviare le traiettorie di un fascio di elettroni, in modo da dar luogo a fenomeni di rifrazione elettronica, analogamente a quanto fanno le l. ottiche per i raggi luminosi.
L. d’ingrandimento
Detta anche microscopio semplice, è una l. convergente utilizzata ponendo l’oggetto tra il fuoco e la l.; l’immagine così prodotta è virtuale, diritta e ingrandita.
L. gravitazionale
In astronomia, particolare configurazione di un campo gravitazionale molto intenso (per es., generato da una galassia gigante) che deflette e focheggia la radiazione elettromagnetica che l’attraversa.
Medicina
L. a contatto
Sottile l. di piccole dimensioni da applicarsi direttamente alla superficie anteriore del bulbo oculare, senza sussidio di alcun sostegno, per correggere vizi di rifrazione dell’occhio. Le l. a contatto attuali (l. corneali) sono di dimensioni pari all’incirca a quelle della cornea alla quale aderiscono perfettamente per tutta la loro superficie; si dividono in rigide e morbide. Le l. rigide, realizzate in polimetilmetacrilato, caratterizzato da buone proprietà ottiche, leggerezza, facilità di lavorazione, possono però provocare disturbi (alterazioni epiteliali), scalfitture della cornea (se piccolissimi corpi estranei duri s’interpongono tra lente e cornea) e presentano una scarsa permeabilità all’ossigeno. Le l. morbide sono costituite da idrogeli acrilici vetrosi e fragili allo stato secco, ma che divengono teneri e pieghevoli in seguito all’assorbimento di acqua. La presenza dell’acqua all’interno della massa polimerica favorisce l’assorbimento dell’ossigeno. Il loro operare è proporzionale al loro contenuto in acqua (che può andare dal 30 all’80%), escludono la possibilità d’interposizione di sostanze estranee, sono meglio tollerate, non provocano alterazioni della cornea; quelle a elevata idrofilia (contenuto in acqua fino all’80%) possono essere mantenute a contatto della cornea ininterrottamente per lunghi periodi. Ogni tipo di l. corneale ha una sua precisa indicazione per la correzione dei vari vizi di rifrazione, che compete solo al medico oculista.
L. intraoculare
Piccola l. acrilica che viene inserita all’interno dell’occhio, a scopo ottico, per migliorare la visione, senza l’ausilio di occhiali correttivi, in alcuni vizi di rifrazione quali l’ofachia e la miopia. Può essere inserita all’interno della camera anteriore dell’occhio, oppure a cavallo dell’iride su cui viene fissata, o, nella maggior parte dei casi, nella camera posteriore a livello della capsula posteriore del cristallino, nei casi di intervento per estrazione della cataratta. La sede anatomica dell’impianto, il potere diottrico, corrispondente al difetto di rifrazione che si vuol correggere, i parametri anatomo-fisiologici dell’occhio del paziente, determinano la scelta e le caratteristiche della l. intraoculare da utilizzare con particolare riguardo ad alcuni procedimenti tecnici che consentono l’assorbimento dei raggi ultravioletti o la possibilità di una correzione ottica monofocale, bifocale o multifocale.
Tecnica
In idraulica, l. idrometrica, apparecchio limitatore di portata consistente in un disco di porcellana con un foro al centro, di diametro regolabile in modo da determinare una portata prestabilita per la normale pressione d’esercizio. L’uso di tale apparecchio, poco preciso, è oggi riservato a distribuzioni di importanza limitata.
Zoologia
L. cristallina (o cristallino o l.)
È la parte dell’apparato rifrangente dell’occhio dei Vertebrati, grazie al quale è possibile l’accomodamento visivo.
Si sviluppa da una proliferazione dell’ectoderma che ricopre l’abbozzo oculare o vescicola ottica e, come bottone solido o come vescicola lentogena, si distacca poi dall’ectoderma, andando ad allogarsi nella cavità della cupola o calice ottico. Successivamente la vescicola lentogena si differenzia: le cellule cubiche della parte anteriore vanno appiattendosi e costituiscono l’epitelio anteriore della l.; quelle della parete posteriore, allungandosi, si trasformano nelle fibre del cristallino, che invadono la cavità della vescicola, obliterandola. A misura che l’abbozzo si accresce, nuove fibre si formano e si moltiplicano in corrispondenza del suo equatore, disponendosi come tante lamelle parallele che, perdendo il loro nucleo, si dispongono al centro, mentre l’epitelio anteriore si estende tutto intorno a quello che è divenuto il corpo traslucido ed elastico della l., formandone la capsula elastica. Da principio vascolarizzata, la l. successivamente è del tutto priva di vasi.
Presenta forma, grandezza, consistenza varie nei diversi gruppi: nei Mammiferi è biconvessa, quasi sferica in alcuni di essi; nell’Uomo, e nei Cetacei, la curvatura posteriore è molto più pronunciata. Le sue dimensioni sono notevoli nei pesci e in genere negli animali notturni; in generale è tanto più molle quanto maggiore è l’ampiezza d’accomodazione. Possiede un nucleo centrale differenziato nei Sauropsidi e assai di più nei Mammiferi, nei quali le lamelle della l. cristallina sono tanto più dense quanto più profonde, distinte in una parte corticale e una parte nucleare della l., caratterizzate da un diverso indice di rifrazione. Nelle varie classi di Vertebrati le connessioni della l. sono diverse: nei Mammiferi, e in genere in tutti gli Amnioti, dalla periferia della l. si dipartono fibre del cosiddetto legamento ciliare (zonula ciliare o di Zinn) che la tengono sospesa ai processi ciliari, ed è per effetto di tali muscoli ciliari (circolari e meridionali) che la l., posta dietro l’iride, si sposta avanti e indietro, modificando la sua forma e di conseguenza variando il fuoco e permettendo così l’accomodazione. Nei pesci, dove mancano i muscoli ciliari, si ha un legamento sospensore della l. e un muscolo retrattore di essa o muscolo della campanula di Haller (processo falciforme); muscoli protrattori della l. si hanno anche negli Anfibi. L’accomodazione si compie infatti, nei pesci, non mediante variazioni di curvatura della l., ma per il suo avvicinamento e allontanamento dalla retina.
Una l. cristallina caratterizza anche l’occhio di molti invertebrati come quello degli Anellidi Policheti, e quello dei Molluschi (Cefalopodi), che presenta una grande rassomiglianza con l’occhio dei Vertebrati.
Per la l. cristallina nell’occhio umano ➔ cristallino.