ingrandimento

fig. 1

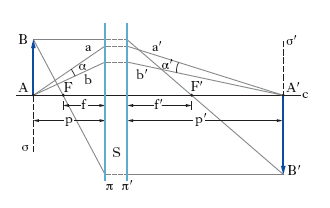
In fisica, termine usato correntemente per indicare la proprietà, e misurare la capacità, di un sistema ottico di dare di un oggetto immagini più grandi di quelle che si hanno dall’osservazione a occhio nudo. In ottica, ingrandimento angolare: sia A′ (fig. 1) l’immagine di un punto A fornita da un sistema ottico S stigmatico per A: a ogni coppia di raggi a, b, incidenti, uscenti da A, corrisponde una coppia a′, b′ di raggi emergenti, incrociantisi in A′. Il rapporto G_a=α′/α fra l’angolo α′ dei due raggi emergenti e quello α dei due corrispondenti raggi incidenti, se conserva invariato il suo valore al variare della coppia di raggi che si considera, diviene un elemento caratteristico del sistema nei riguardi dei punti A e A′ e ha il nome di i. angolare relativo ai punti A e A′. Ingrandimento lineare: siano σ e σ´ due piani coniugati rispetto a un sistema ottico S (fig. 1) che sia per essi ortoscopico (cioè di ogni figura contenuta in σ dia un’immagine simile in σ′): i due piani sono ortogonali all’asse ottico c. Il rapporto G_lt=A′B′/AB tra la lunghezza dell’immagine A′B′ del segmento AB e la lunghezza di AB, se conserva invariato il suo valore al variare di AB su σ (quindi di A′B′ su σ′), diviene un elemento caratteristico del sistema rispetto alla coppia di piani considerati e ha il nome di ingrandimento lineare trasversale dell’immagine, rispetto all’oggetto.

Si parla invece di ingrandimento lineare longitudinale, G_ll, se ci si riferisce a segmenti coniugati paralleli all’asse del sistema. Se ci si pone nell’approssimazione di Gauss (raggi parassiali, sistema di piccola apertura), si trova che è G_ll G_a=−G_lt, G_a essendo l’i. angolare; in particolare, per un sistema diottrico centrato, l’i. lineare trasversale, o i. lineare propriamente detto, vale f/(p−f) = (p′−f′)/f′ ove p è la distanza dell’oggetto dal primo piano principale di traccia π, p′ è la distanza dell’immagine dal secondo piano principale π′, f ed f′ sono le distanze focali del sistema, F e F′ essendo i fuochi. L’i. lineare è assunto spesso come grandezza priva di segno; in realtà, esso, come risulta dalle relazioni prima scritte, può essere positivo oppure negativo, a seconda dei valori di p e p′ in rapporto a f e f′: come si dimostra, esso è positivo oppure negativo a seconda che il sistema dia di un oggetto un’immagine capovolta oppure diritta.

fig. 2

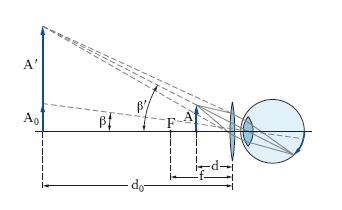
Ingrandimento visuale Per una lente oculare (in generale, per uno strumento ausiliario dell’occhio: cannocchiale, microscopio ecc.) si chiama i. visuale il rapporto tra l’angolo β′ sotto cui è vista dall’occhio l’immagine A′ dell’oggetto A data dalla lente e l’angolo β sotto cui l’oggetto sarebbe visto a occhio nudo (fig. 2). In generale, l’i. visuale I varia, a parità di altre condizioni, al variare della distanza dell’oggetto dalla lente o dallo strumento. Per le lenti oculari, per es. per le cosiddette ‘lenti d’ingrandimento’, risulta peraltro comodo ed espressivo dare un i. che prescinda dalle particolari condizioni d’impiego; è così definito per esse un i. convenzionale I_c per il quale si intende che nella visione con la lente l’oggetto, posto a distanza d, sia quasi nel fuoco anteriore F (e quindi che l’immagine, virtuale, si formi a distanza molto grande dalla lente), e che nella visione a occhio nudo l’oggetto (A_o) si trovi alla distanza della visione distinta d_o, assunta pari a 250 mm; se si misura la distanza focale f della lente in millimetri, è allora I_c=250/f.