distanza

La lunghezza del tratto di linea retta che congiunge due punti.

Astronomia

Storia

fig. 1

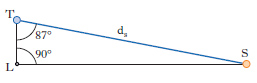
I primi tentativi di misurare le distanze astronomiche furono effettuati dagli antichi Greci. La fig. 1 illustra il metodo con cui Aristarco di Samo (3° sec. a.C.) e Ipparco (2° sec. a.C.) ottennero, per la prima volta, una stima della distanza Terra-Sole (d_s). Quando la Luna è nel primo o ultimo quarto, il triangolo TLS, che ha per vertici la Terra (T), la Luna (L) e il Sole (S), è rettangolo in L. Osservando le posizioni della Luna e del Sole nel cielo, Aristarco valutò inoltre che l’angolo LTS misurasse 87° e, quindi, ricavò TS/TL=20 (in realtà, il rapporto delle distanze Terra-Sole e Terra-Luna è assai più grande, ≃390, perché LTS≃89°51′). Ipparco, con un metodo ingegnoso basato sull’osservazione delle eclissi lunari, trovò TL=386.000 km (in stupefacente accordo col valore, 387.600 km, della distanza media Terra-Luna, oggi misurata con tecniche ben più raffinate), e ne dedusse d_s=8·10⁶ km. Soltanto nel 16° sec., N. Copernico riuscì a valutare con discreta precisione le distanze relative dal Sole dei 5 pianeti noti (Mercurio, Venere, Marte, Giove e Saturno). Nei secoli successivi, lo sviluppo del metodo della parallasse trigonometrica consentì di misurare con crescente precisione le distanza dei pianeti e del Sole; già intorno al 1670, G.D. Cassini otteneva per quest’ultima il valore 140·10⁶ km, che è solo del 7% inferiore al valore oggi accettato. Per quanto riguarda le distanze stellari, il primo successo fu ottenuto nel 1838 da F.W. Bessel, che, applicando il metodo della parallasse, riuscì a misurare la distanza della stella 61 Cigni. In questo campo, tuttavia, si progredì lentamente: alla fine dell’Ottocento si era riusciti a determinare con discreta precisione la distanza di appena una ventina di stelle relativamente vicine al Sole. I successivi progressi realizzati nel 20° secolo sono stati resi possibili soprattutto dallo sviluppo di indicatori di distanza, che permettono di valutare le distanze di oggetti lontanissimi ai quali non è applicabile il metodo della parallasse.

Distanza nel sistema solare

fig. 2

Distanza di un pianeta

Tradizionalmente, la distanza di un pianeta si determina col metodo della parallasse, illustrato in fig. 2. Sia XY il diametro della Terra perpendicolare alla retta CP, congiungente il centro C della Terra col pianeta P. Un osservatore, situato nel punto X, vede il pianeta, sullo sfondo delle stelle fisse, nella direzione XX′; 12 ore più tardi, a causa della rotazione della Terra, l’osservatore si trova in Y e vede il pianeta nella direzione YY′. Si misura così l’angolo XPY, la cui metà ϑ=1/2 XPY prende il nome di parallasse del pianeta (il valore di ϑ così ottenuto deve essere corretto, tenendo conto dello spostamento della Terra e del pianeta, sulle rispettive orbite, nell’intervallo di tempo fra le due osservazioni). Noto ϑ e conoscendo il raggio della Terra (R_T=6378 km), dal triangolo CXP si ricava la distanza d_p del pianeta: d_p=R_T/tg ϑ. Oggi, le distanze dei pianeti si ottengono con precisione assai più elevata usando la tecnica del radar: se Δt è l’intervallo di tempo trascorso fra l’istante in cui viene inviato l’impulso di onde radio e quello in cui viene ricevuto il segnale riflesso dal pianeta, si ha d_p=1/2c Δt (dove c è la velocità della luce).

Distanza Terra-Sole

Sono due i metodi classici con cui si misura la distanza (d_s) Terra-Sole.

fig. 3

Metodo della velocità orbitale

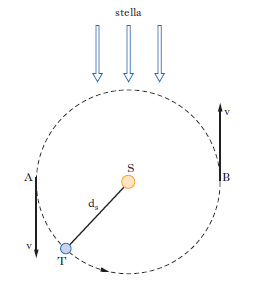
A causa dell’effetto Doppler, una riga di frequenza ν₀ dello spettro di una stella viene osservata quando la Terra è in A (fig. 3) a una frequenza maggiore (ν₀+ν_d) e quando la Terra è in B, a una frequenza minore (ν₀−ν_d). La velocità orbitale della Terra è allora: v=cν_d/ν₀≃29,8 km/s. Conoscendo il periodo di rivoluzione della Terra (T=31,56·10⁶s), si ricava: d_s=vT/2π.

fig. 4

Metodo trigonometrico

L’applicazione diretta del metodo della parallasse alla determinazione della distanza Terra-Sole non fornisce risultati molto precisi. Si preferisce allora ricorrere a un metodo indiretto, illustrato in fig. 4. Nel triangolo TPS, che ha per vertici la Terra (T), un pianeta (P) e il Sole (S), sono noti: il lato TP, che è la distanza d_p del pianeta ottenuta sopra; l’angolo PTS, che può essere misurato; il rapporto PS/TS, che si deduce dalla III legge di Keplero, conoscendo i periodi di rivoluzione della Terra e del pianeta. Si ricava allora la lunghezza del lato TS, cioè ds.

Le misure più precise, che si avvalgono delle determinazioni delle distanze planetarie ottenute con la tecnica radar, danno per la distanza media Terra-Sole (che si assume come unità astronomica, UA): 1 UA=1,49598·10⁸ km.

Distanza nella Galassia

fig. 5

Metodo della parallasse trigonometrica

Il metodo della parallasse, usato per misurare le distanze dei pianeti, può essere applicato anche alla misura delle distanze stellari. Tuttavia, data l’enorme distanza delle stelle, il diametro della Terra costituisce una ‘base’ troppo piccola per la determinazione della parallasse: si utilizza, allora, al suo posto, il diametro dell’orbita della Terra, come mostrato in fig. 5. Nella figura è considerato il caso più semplice in cui la stella è situata nella direzione del polo nord eclittico, sicché la retta SA, congiungente il Sole (S) con la stella (A), è perpendicolare al piano dell’orbita della Terra (l’eclittica). Nel corso dell’anno, a causa del moto di rivoluzione della Terra, l’osservatore vedrà la stella descrivere nel cielo un’orbita circolare di raggio angolare p≃tg p=d_s/d_A (dove d_A è la distanza della stella e d_s=1 UA). Misurando p (detta parallasse trigonometrica della stella) si ricava d_A. Se la stella non si trova nella direzione polare la sua traiettoria apparente nel cielo è un’ellisse, anziché una circonferenza, e la parallasse p viene definita come il semiasse angolare maggiore dell’orbita. Alle misure di parallasse stellare si devono apportare varie correzioni, la più importante delle quali è quella relativa al fenomeno della aberrazione astronomica. Dalla parallasse viene derivata l’unità di misura delle distanze più comunemente usata in astronomia, il parsec (pc), definito come la distanza alla quale una stella avrebbe una parallasse di 1 secondo d’arco. Si trova: 1 pc=206.265 UA=3,08568∙10¹⁶ m=3,2615 anni-luce. La stella più vicina al Sole, α-Centauri, ha una parallasse di 0,76″ e quindi una distanza d_A=1,32 pc (4,3 anni-luce). Vi sono 39 stelle che hanno parallasse maggiore di 0,2″ (d_A≤5 pc); circa 2000 che hanno parallasse maggiore di 0,04″ (d_A≤25 pc). Per queste stelle si ottengono le distanze con discreta precisione. Per le stelle più lontane gli errori diventano troppo grandi, tuttavia, pur non essendo possibile misurare la distanza di singole stelle, si riesce, fino quasi a 100 pc, a stimare la distanza media di gruppi di stelle.

Metodo della parallasse fotometrica

La magnitudine apparente (m), la magnitudine assoluta (M) e la distanza (d_A) di una stella sono legate fra loro dalla relazione:

[1] m−M=5log (d_A)−5,

dove d_A è misurata in parsec (si noti che questa formula è valida solo in assenza di assorbimento: in caso contrario, al secondo membro occorre aggiungere un termine che dà l’estinzione, in magnitudini, dovuta al mezzo interstellare). Se sono note m e M, la [1] permette di ricavare d_A. Alla distanza così ottenuta si associa un valore della parallasse, chiamato parallasse fotometrica. Le incertezze del metodo dipendono soprattutto dalla difficoltà di stimare con precisione la magnitudine assoluta. Questa viene dedotta, di solito, dalle caratteristiche spettrali della stella, utilizzando il diagramma di Hertzsprung-Russell (➔ stella).

Metodo di Baade-Wesselink

Si applica alle variabili periodiche (stelle, come le Cefeidi e le RR Lirae, la cui luminosità varia periodicamente nel tempo). La luminosità di una stella, di raggio r e temperatura superficiale T, è L=4πr² σ T⁴, dove σ è la costante di Stefan-Boltzmann. Di conseguenza, se di una stella variabile si conosce la temperatura (ottenuta osservandone l’indice di colore), dalle variazioni della sua magnitudine apparente si può risalire alle corrispondenti variazioni relative del raggio, ovvero al rapporto Δr/d_A, fra la variazione assoluta del raggio e la distanza. Misurando poi il periodo e la velocità delle oscillazioni (quest’ultima dedotta dallo spostamento Doppler delle righe spettrali) si ottiene, in modo indipendente, la variazione assoluta (Δr) del raggio. La conoscenza simultanea di Δr/d_A e Δr permette, infine, di ricavare la distanza.

Distanze extragalattiche

Distanze extragalattiche

La misura delle distanze extragalattiche si basa sui cosiddetti indicatori di distanza. La distanza di una galassia può essere valutata con notevole precisione se in essa si individua una Cefeide e se ne misura il periodo. La relazione periodo-luminosità, che caratterizza tali stelle, permette infatti di ricavare la magnitudine assoluta, dalla quale, col metodo della parallasse fotometrica, si deduce la distanza.

Diritto

Distanze legali tra costruzioni

In diritto civile, limiti minimi di distanza che devono separare costruzioni, piantagioni, scavi, muri, fossi e siepi posti su fondi confinanti. In particolare, tra edificio ed edificio, muro e muro, vi deve essere una distanza di almeno 3 m, che i regolamenti comunali possono aumentare, ma mai diminuire (art. 873 c.c.). È tuttavia prevista una deroga per favorire il superamento e l’eliminazione delle barriere architettoniche negli edifici privati (art. 3, l. 13/1989, come modificato dall’art. 1 l. 62/1989). In materia di distanza si applica il cosiddetto principio della prevenzione, in forza del quale chi per primo costruisca su un fondo confinante con un altro può scegliere se costruire sul confine, o alla distanza normativamente prevista dal fondo contiguo, o infine a una distanza inferiore alla metà rispetto a quella complessiva risultante. Il proprietario confinante nel primo caso potrà costruire in aderenza (ma senza appoggiare il proprio edificio) all’opera preesistente (art. 877), oppure potrà ottenere la comunione del muro appoggiando il suo edificio, e pagando metà del valore del muro (art. 875); nell’ultimo caso potrà chiedere la comunione del muro solo allo scopo di fabbricare contro il muro stesso, pagando sia il valore della metà del muro, sia il valore del suolo da occupare con la nuova costruzione, salvo che il proprietario che ha costruito per primo preferisca estendere il suo muro fino al confine. In proposito le sezioni unite della Corte di cassazione hanno stabilito che la facoltà del prevenuto di chiedere la comunione forzosa del muro non situato sul confine non è impedita dal fatto che su detto muro siano state aperte delle vedute. I pozzi, le cisterne, le fosse ecc. devono essere distanti almeno 2 m dal confine (art. 889); i canali e i pozzi devono essere distanti dal confine tanto quanto sono profondi (art. 891). Salvo diverse disposizioni locali, gli alberi di alto fusto devono essere distanti almeno 3 m; gli alberi il cui tronco prima di dipartirsi non supera l’altezza media di 3 m devono essere distanti 1,5 m; gli altri alberi e le piccole piante fruttifere, 0,5 m (art. 892). Se gli alberi vengono piantati a distanza inferiore alla legale il proprietario del fondo contiguo può esigere la loro estirpazione (art. 894), può costringere il proprietario dell’albero piantato a legale distanza a tagliare i rami che sporgono oltre il confine e può recidere egli stesso le radici invadenti. I frutti che cadono naturalmente sul fondo vicino spettano al proprietario di tale fondo, salvi gli usi locali (art. 896). Quando le costruzioni sono di fabbriche, o di depositi nocivi e pericolosi, si deve rispettare la distanza che sia di caso in caso ritenuta necessaria a preservare i fondi vicini da ogni danno (art. 890). Il proprietario che ha subito lesione per violazione delle norme sulle distanze legali può agire contemporaneamente per ottenere sia la riduzione in pristino dello stato dei luoghi, sia il risarcimento del danno causato dall’opera illegittima, considerando però che, dal momento in cui si attua la prima forma di tutela, la seconda copre soltanto i danni provocati dall’opera prima della sua eliminazione.

Geografia

Distanza itineraria

È lo spazio che si deve percorrere per recarsi da un punto a un altro utilizzando le vie di comunicazione disponibili (in genere si tratta di più distanze itinerarie, soprattutto quando esiste una pluralità di mezzi di trasporto). Distanza economica, detta anche distanza-costo, è una grandezza alla cui formazione concorrono sia la distanza itineraria sia il costo unitario di trasporto sia il costo in termini di tempo: più precisamente la distanza economica cresce al crescere della distanza itineraria e del costo unitario e al diminuire della velocità.

Informatica

La distanza tra stringhe binarie, aventi la stessa lunghezza, è il numero di posizioni in cui le due stringhe assumono valore differente (distanza di Hamming). L’operazione XOR tra due stringhe binarie produce come risultato una stringa composta da zero nelle posizioni in cui le stringhe sono eguali e da uno nelle posizioni in cui le stringhe differiscono. Contando il numero di uno nella stringa risultato dell’operazione XOR si ricava la distanza tra le due stringhe: per questo il termine distanza indica anche l’operazione XOR.

Istruzione

Istruzione a distanza

Locuzione usata nell’attività didattica per qualificare funzioni svolte utilizzando reti di comunicazione telematiche e pertanto non soggette all’immediato controllo degli insegnanti.

Matematica

fig. 6

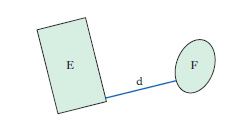
La distanza di due punti, per due punti su un piano o nello spazio, è la lunghezza del segmento di retta che li congiunge. La distanza tra un punto e una retta (o un piano) è la distanza del punto dato dal piede della perpendicolare condotta per il punto alla retta (o al piano). La distanza tra due rette parallele (o tra due piani paralleli) è la lunghezza di un segmento di perpendicolare comune avente gli estremi sulle due rette (sui due piani). La distanza tra due rette sghembe è la distanza tra i due punti in cui le due rette sono tagliate dalla loro unica perpendicolare comune; quest’ultima prende perciò il nome di retta di minima distanza tra le due rette date. Più in generale si chiama distanza di due figure (insiemi di punti) E, F l’estremo inferiore d delle distanze di un punto di E da un punto di F  (fig. 6).

La distanza d  tra due punti, di coordinate cartesiane ortogonali (x₀, y₀, z₀) e (x₁, y₁, z₁), vale:

[1]

Il concetto di distanza tra due punti s’identifica con quello di minimo percorso dall’uno all’altro dei due punti: così, per due punti sulla superficie terrestre, supposta sferica, potrà essere assunta a misura della loro distanza la lunghezza dell’arco di cerchio massimo passante per i due punti e in generale per due punti su una superficie qualsiasi si potrà definire (sotto opportune condizioni) loro distanza la lunghezza dell’arco di geodetica per i due punti (distanza geodetica).

Trasporti

Nella tecnica dei trasporti, e in particolare nella tecnica della circolazione, distanza di sicurezza, la distanza che i veicoli devono mantenere durante la marcia rispetto al veicolo che precede perché sia garantito in ogni caso l’arresto tempestivo e siano evitate collisioni; distanza di leggibilità, la distanza alla quale il conducente di un veicolo in movimento riconosce i simboli o le lettere di una segnalazione stradale; distanza di visibilità, la lunghezza di carreggiata visibile dal conducente di un veicolo in movimento.