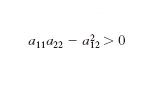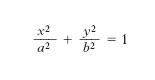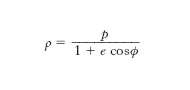ellisse
In geometria, curva piana chiusa che si ottiene segando un cono circolare (retto od obliquo) con un piano non parallelo ad alcuna generatrice. Un caso particolare di e. è da considerarsi la circonferenza.
L’e. è una curva piana del 2° ordine, cioè una conica. In coordinate cartesiane x, y, essa è rappresentata da un’equazione di 2° grado, del tipo a11x2+2a12xy+a22y2+2a13x+2a23y+a33=0, nella quale sia
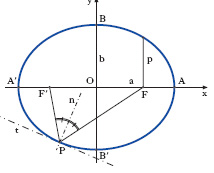
il cui verificarsi significa infatti, dal punto di vista geometrico, che la conica rappresentata dall’equazione scritta non ha punti reali all’infinito. L’e. è una conica a centro: possiede cioè un centro di simmetria, O, dal quale escono due rette, tra loro perpendicolari, che sono assi di simmetria. Siano (fig. 1) A e A′ i punti di incontro con l’e. del primo asse di simmetria, B e B′ i punti di incontro con l’e. del suo secondo asse di simmetria. Supponiamo che essi siano di diversa lunghezza e che la lunghezza 2a di AA′ sia maggiore della lunghezza 2b di BB′. Le rette AA′, BB′ si chiamano allora rispettivamente asse maggiore e asse minore dell’e.; i punti A, A′, B, B′ sono i vertici dell’ellisse. Assumendo come asse delle x l’asse di simmetria A′ A, come asse delle y quello B′ B, l’equazione dell’e. si riduce alla cosiddetta forma canonica:
Punti notevoli rispetto all’e. sono i suoi fuochi F, F′ : cioè i punti situati sull’asse maggiore (detto perciò asse focale) a distanza c=√‾‾‾‾‾‾a2−‾‾b2 dal centro O. L’importanza dei fuochi dal punto di vista elementare risiede nel fatto che «un’e. è il luogo dei punti del piano per i quali la somma delle distanze dai fuochi F, F′ è uguale alla lunghezza 2a dell’asse maggiore». Il rapporto e=c/a〈1 si chiama eccentricità. Per ogni fuoco esiste una retta, perpendicolare all’asse focale (direttrice relativa a detto fuoco), tale che il rapporto delle distanze di un punto dell’e. dal fuoco e da detta retta è una costante uguale a e. L’eccentricità di un’e. è un numero positivo minore dell’unità (per il cerchio e=0).
Di particolare interesse, anche per le applicazioni all’astronomia, è l’ equazione polare di un’e.: scelto il polo in uno dei fuochi e l’asse polare coincidente con l’asse focale e orientato verso il vertice più vicino, essa si scrive
ove il valore di p, parametro dell’e., è dato da b2/a. L’area racchiusa dall’e. si calcola facilmente, ed è uguale a πab.
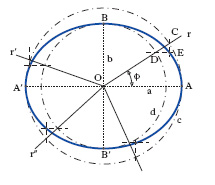
La costruzione per punti di un’e., noti i semiassi a, b, può essere effettuata (fig. 2) disegnando due circonferenze concentriche, una c di raggio a, l’altra d di raggio b, e tracciando i diametri, fra loro perpendicolari, A′ A, B′ B: dal centro O si mandi una semiretta r a incontrare la c in C, la d in D; da C si mandi la perpendicolare ad A′ A, da D la perpendicolare a B′ B, il punto d’incontro E delle due perpendicolari è un punto dell’e., questa viene descritta completamente ripetendo la costruzione per diverse semirette r′, r″,… uscenti da O. Di semplice realizzazione è la cosiddetta ‘costruzione del giardiniere’: un filo di lunghezza 2a (asse maggiore dell’e.) sia fissato agli estremi a due paletti infissi nel terreno; presa un’asta, la si fa scorrere sul terreno lungo il filo in modo che questo resti sempre teso; ottenendo così il tracciamento di un’e. avente i fuochi nei punti in cui è fissato il filo.