geometria

In senso ampio e generico, ramo della matematica che studia lo spazio e le figure spaziali.

Cenni storici
L’antichità

- L’origine della g. è legata a concreti problemi di misurazione del terreno (nacque a scopi agrimensori nella zona del delta del Nilo); si trattava quindi essenzialmente di una g. empirica, consistente in un certo numero di regole pratiche per la misurazione e la costruzione di alcune figure più semplici (angoli retti, triangoli ecc.). Ma già l’antica civiltà greca vide il sorgere della g. come scienza razionale, staccata da ogni esigenza applicativa e da ogni empiricità di metodo, e volta a studiare sistematicamente le proprietà delle figure del piano e dello spazio, ordinandole in una successione di stretta dipendenza logica. Euclide, infatti, raccogliendo tutto il patrimonio di sapere costruito da studiosi che lo precedettero (Pitagora, Talete, Eudosso di Cnido ecc.), offre con i suoi Elementi, in 13 libri, il primo esempio di quello che oggi diremmo un trattato scientifico, per il metodo rigorosamente deduttivo che fa discendere ogni proposizione da proposizioni precedentemente stabilite, a partire da un nucleo iniziale di proprietà ‘evidenti’ (assiomi) riguardanti alcuni oggetti primitivi (punto, retta, piano). Per quanto abbiano avuto, presso gli antichi, minore risonanza, debbono tuttavia essere ricordati anche gli studi di Apollonio sulle coniche e quelli di Archimede sul cerchio e sulla sfera. Le successive scuole matematiche, in Grecia e altrove, non portarono sviluppi di rilievo alla geometria.

L’età moderna

- Bisogna giungere al Rinascimento italiano per individuare i germi di nuove idee che porteranno in seguito alla nascita della g. proiettiva e descrittiva. Una svolta decisiva nella visione dei problemi geometrici si ebbe con la g. analitica di Cartesio (17° sec.), che aprì un periodo nuovo nella storia della g. e della stessa matematica. Il metodo cartesiano delle coordinate, infatti, permise da un lato di trattare sistematicamente i problemi geometrici con gli strumenti dell’algebra e del calcolo infinitesimale, e d’altro lato di arricchire l’algebra e l’analisi di ‘contenuti geometrici’ che illuminano molti fatti e situazioni algebriche e analitiche. Ebbe così inizio un fervore di ricerche e un rinnovarsi di metodi che si sarebbero protratti fino al 19° sec., per culminare poi nelle ricerche di g. differenziale di K.F. Gauss e B. Riemann. Nel frattempo, gli studi di G. Desargues sulle coniche preparavano il terreno alla fondazione della futura g. proiettiva di J.-V. Poncelet.

Questo fiorire di risultati e di metodi nuovi doveva portare, attorno alla metà del 19° sec., a un modo nuovo di concepire la g. mettendo in crisi le idee tradizionali e dando così inizio al periodo moderno della g. stessa. Di ciò fu elemento determinante la dimostrazione della coerenza logica delle g. non euclidee, data da J. Bolyai e N.I. Lobačevskij, la quale, chiudendo definitivamente i tentativi di far discendere il 5° postulato di Euclide dalle precedenti proposizioni euclidee, ne dimostrava l’indipendenza logica. La possibilità di escludere tale postulato dal novero delle proposizioni che stanno alla base della g., dando vita a nuove g. lontane dalla comune intuizione, ma ugualmente coerenti, interrompeva la tradizione millenaria che aveva praticamente identificato la g. e il suo contenuto con i modelli euclidei. Dalla precedente concezione della g. come sistema assiomatico-deduttivo, nel quale le proposizioni iniziali, lungi dal poter essere liberamente scelte, esprimono proprietà evidenti, e quindi non discutibili, dello ‘spazio’ – concezione che rimase sostanzialmente invariata anche attraverso il rinnovamento portato dal metodo cartesiano – si passa alla nuova visione della g. come scienza ipotetico-deduttiva che può scegliere i suoi principi con una certa libertà tra quelli che vengono suggeriti, ma non imposti, dalla nostra esperienza con il mondo circostante. Ciò porta da un lato al nascere di problemi nuovi e delicati, come quello della compatibilità logica dei postulati, problemi che vanno inquadrati e inseriti nel più vasto movimento di rinnovamento della matematica moderna che va sotto il nome di ‘critica dei fondamenti’, e d’altro lato a un radicale mutamento del concetto stesso di spazio come ambiente di una determinata g., tanto che moltissimi dei risultati e dei procedimenti che oggi si fanno rientrare nella g. non sono suscettibili di rappresentazione o di interpretazione nello spazio abituale.

Occorre anche ricordare l’influenza esercitata sui moderni orientamenti nella impostazione della g. dal cosiddetto programma di F. Klein, enunciato a Erlangen nel 1872, e perciò detto anche programma di Erlangen. Questo presenta una g. come studio delle proprietà degli enti geometrici che rimangono invariate operando sugli enti stessi mediante le trasformazioni di un certo gruppo, il gruppo fondamentale di quella geometria. Da questo punto di vista la g. euclidea studia le proprietà invarianti rispetto al gruppo dei movimenti, la g. proiettiva quelle invarianti rispetto al gruppo delle proiettività ecc.

Il 19° sec., a giusto titolo considerato il secolo d’oro della g., oltre alle g. non euclidee ha visto la formazione e lo sviluppo di altre importanti branche della g.: la g. proiettiva, organizzata in forma sistematica e definitiva da Poncelet, e, a questa strettamente legata, la g. descrittiva di G. Monge; la g. differenziale, fondata da Gauss e Riemann, che studia le proprietà differenziali delle curve, delle superfici e delle varietà a più dimensioni e ha dato poi origine al calcolo differenziale assoluto e al calcolo tensoriale; la g. algebrica (iniziata, per le curve, da Riemann e fiorita poi specialmente in Italia con G. Veronese, L. Cremona ecc.), che studia le proprietà invarianti per trasformazioni birazionali. Si tratta di teorie che, pur sotto la comune denominazione di g., sono tra loro fortemente differenziate, anche per i profondi legami con altre diverse parti della matematica, tanto che spesso sono passate a formare capitoli autonomi della scienza matematica, o a ricoprire addirittura un intero settore della matematica; così è accaduto per la topologia, che, sorta inizialmente come analysis situs, cioè come g. di posizione, ha oggi assunto il ruolo di uno dei rami fondamentali della matematica moderna.

Nel 20° sec. la g. ha avuto notevoli sviluppi, soprattutto nell’area che si occupa dello studio e della classificazione delle varietà.

G. elementare

Detta anche g. metrica (in senso elementare), si identifica praticamente con la g. euclidea del piano e dello spazio. Gran parte della g. elementare si occupa delle proprietà metriche delle figure, quelle legate cioè alla loro estensione; in quanto tale, essa si può pensare, nell’indirizzo di Klein, come quella g. che studia le proprietà delle figure invarianti rispetto al gruppo dei movimenti. Per es., appartiene alla g. euclidea la proprietà che «le diagonali di un quadrato sono perpendicolari», perché trasformando il quadrato con un movimento si ottiene ancora un quadrato, le cui diagonali sono le trasformate delle diagonali del primo e sono pertanto perpendicolari. Si fa rientrare nella g. elementare anche lo studio del comportamento delle figure rispetto alle similitudini, anziché rispetto ai movimenti.

La trattazione della g. negli Elementi di Euclide è di tipo assiomatico-deduttivo: introdotti gli enti primitivi – punto, retta e piano – seguono i 5 assiomi (presentati come proprietà evidenti) che equivalgono agli enunciati seguenti: 1) per due punti distinti passa una retta e una sola; 2) ogni segmento si può prolungare indefinitamente; 3) si può tracciare, su un dato piano, una circonferenza di centro arbitrario e raggio arbitrario; 4) tutti gli angoli retti sono uguali; 5) due rette che formino con una terza, da una stessa parte, angoli interni la cui somma sia minore di un angolo piatto, prolungate da quella parte si incontrano (questa proposizione – il 5° postulato – equivale alla unicità della parallela per un punto dato a una retta data). Le proposizioni e i teoremi che costituiscono la g. euclidea non sono che lo sviluppo logico di tali premesse secondo un metodo strettamente deduttivo. Nella concezione euclidea gli enti primitivi (punto, retta e piano) sono astrazioni di enti materiali che sono oggetto della nostra esperienza quotidiana (il punto: corpo piccolissimo, di dimensioni trascurabili; la retta: spigolo molto pronunciato, che si pensi prolungato indefinitamente; ecc.).

La situazione della g. elementare secondo la critica moderna è invece di tipo ipotetico-deduttivo e differisce profondamente dalla precedente, tra l’altro, proprio nella concezione degli enti primitivi, i quali vengono introdotti in modo puramente astratto, nominale, senza essere definiti, e prendono vita, per così dire, solo attraverso i postulati cui devono soddisfare (si dice anche che i postulati definiscono ‘implicitamente’ gli enti primitivi). Tra le diverse sistemazioni della g. elementare secondo questa veduta moderna, degna di nota è quella di D. Hilbert, nella quale i postulati che caratterizzano i punti, le rette e i piani sono suddivisi in 5 gruppi come segue: 1) postulati di appartenenza (per es., due punti distinti individuano una retta, che ne contiene infiniti); 2) postulati di ordinamento (per es., se A e C sono punti di una retta, esiste sopra essa un punto B situato tra A e C); 3) postulati di congruenza (per es., due triangoli, che hanno due lati e l’angolo compreso uguali, hanno rispettivamente uguali anche gli altri due angoli); 4) postulato delle parallele (per un punto non appartenente a una retta passa una e una sola retta parallela alla retta data: è il 5° postulato di Euclide); 5) postulati di continuità (per es., dati comunque due segmenti, esiste un multiplo dell’uno che sia maggiore dell’altro: è il postulato di Archimede). A questo punto sorge il problema della compatibilità logica del sistema di postulati enunciati, problema che viene ricondotto da Hilbert alla costruzione di opportuni modelli della g. in questione basati sull’algebra e sull’analisi.

Le g. secondo la classificazione di Klein

Il criterio di Klein per classificare le g., enunciato nel programma di Erlangen, consiste nel porre a fondamento di una g. un gruppo di trasformazioni, detto gruppo fondamentale di tale g., e nell’assegnare a tale g. le proprietà delle figure che rimangono invariate rispetto a tutte le trasformazioni del gruppo. Così, per es., la g. elementare si può inquadrare in questa veduta, pensandola come lo studio delle proprietà delle figure geometriche che si mantengono inalterate rispetto al gruppo dei movimenti, proprietà cioè che sono comuni a una data figura F e a tutte quelle F′, F″ ecc., che da essa si ottengono per effetto di un qualsiasi movimento rigido; esempi di tali proprietà sono: la perpendicolarità tra due rette, il fatto che una figura sia un cerchio di dato raggio, o che sia un triangolo di lati assegnati ecc. In definitiva, figure, come F, F′, F″, che siano trasformabili l’una nell’altra mediante un movimento, cioè che siano da considerarsi dotate delle stesse proprietà geometriche, sono figure che, nell’ambito della g. elementare, vengono dette tra loro uguali (o sovrapponibili), vale a dire la trasformabilità di una figura nell’altra mediante una trasformazione del gruppo (un movimento) coincide con la loro uguaglianza secondo la g. elementare. Tale circostanza ha una ragion d’essere profonda perché le proprietà algebriche di un gruppo hanno un perfetto riscontro nelle proprietà formali dell’uguaglianza. Fissato infatti un gruppo G di trasformazioni operanti, per es., nel piano, conveniamo di dire che una figura piana F è equivalente, rispetto a G, a un’altra figura F′quando esiste una trasformazione T di G che muta F in F′. Siccome nel gruppo esistono la trasformazione inversa T⁻¹, la trasformazione identica e il prodotto di due trasformazioni, segue che l’equivalenza rispetto a G gode delle proprietà riflessiva, simmetrica e transitiva. La scelta del gruppo da porre a base di una determinata g. equivale così alla scelta di un criterio di uguaglianza tra le figure geometriche; tale criterio coincide con l’ordinaria nozione di uguaglianza nel caso della g. elementare, ma ne differisce in altri tipi di g.: così in g. proiettiva il criterio è l’equivalenza, o uguaglianza, proiettiva (due coniche irriducibili, per es., sono uguali dal punto di vista proiettivo, perché esiste sempre una proiettività che porta l’una nell’altra) e il relativo gruppo fondamentale, il gruppo delle proiettività; nella g. affine il ruolo analogo è sostenuto dal gruppo delle affinità; nella g. algebrica dal gruppo delle trasformazioni birazionali; nella topologia dal gruppo degli omeomorfismi.

Tipi e indirizzi di geometria

G. affine È l’insieme delle proprietà delle figure di un piano, o dello spazio, o di un iperspazio, le quali sono invarianti rispetto alle affinità, cioè rispetto a quelle omografie che mutano in sé una prefissata retta, o piano, o iperpiano (retta, piano, iperpiano improprio o all’infinito). Sono nozioni di g. affine: il parallelismo, il punto medio di un segmento (sebbene non lo sia la distanza tra due punti), il baricentro geometrico, il centro di una conica ecc. Si inquadra nella classificazione di Klein, assumendo come gruppo fondamentale il gruppo delle affinità.

G. algebrica Studio delle proprietà degli enti algebrici (curve, superfici, varietà), le quali sono invarianti rispetto alle trasformazioni birazionali (il relativo gruppo fondamentale, nella classificazione di Klein, è il gruppo delle trasformazioni birazionali). È una proprietà di g. algebrica, per es., il fatto che una curva sia razionale, cioè che le coordinate del punto variabile sopra essa siano funzioni razionali di un parametro: è un concetto di g. algebrica, in quanto ogni trasformata birazionale di quella curva risulta anch’essa una curva razionale. Sono di pertinenza della g. algebrica lo studio delle trasformazioni birazionali (tra varietà qualsiasi) e cremoniane (tra spazi lineari); la determinazione di caratteri e di enti invarianti per trasformazioni birazionali, quali la serie canonica e il genere per una curva, i sistemi canonici, le serie di equivalenza, genere e plurigeneri e irregolarità per superfici e varietà di dimensione superiore. Notevole sviluppo ebbe la g. algebrica delle superfici e anche delle varietà a opera della scuola italiana (Cremona, C. Segre, E. Bertini, G. Castelnuovo, F. Enriques, F. Severi), che operò con metodi ‘algebrico-geometrici’, portandovi una caratteristica impronta di originalità.

Tra i problemi più importanti di cui si è occupata la g. algebrica c’è il classico problema dello scioglimento delle singolarità, cioè della costruzione di una trasformata birazionale di una varietà algebrica assegnata, la quale risulti priva di singolarità. H. Hironaka ha dimostrato nel 1964 che ogni varietà algebrica complessa ammette una risoluzione delle singolarità riconducendo il problema della classificazione alle varietà proiettive non singolari. Mentre la classificazione delle superfici è giunta a un notevole livello, non altrettanto può dirsi per le varietà di dimensione superiore; soltanto nel 1989 S. Mori ha ottenuto la classificazione delle varietà a tre dimensioni. Oggi le ricerche di g. algebrica si valgono dei più moderni strumenti quali l’algebra e la topologia algebrica; si parla quindi di una ‘g. algebrica moderna’, o anche ‘g. algebrica astratta’, per distinguerla dalla ‘g. algebrica classica’. Nella matematica moderna, e in particolare nella g. differenziale, sono rilevanti i gruppi topologici di Lie, gruppi di trasformazioni analitiche di uno spazio in sé (➔ gruppo; Lie, Sophus; topologia). G. analitica Metodo che permette di tradurre sistematicamente problemi e questioni geometriche in problemi o questioni algebriche o analitiche, o viceversa, in modo da poter risolvere problemi geometrici con i mezzi dell’analisi, ovvero problemi analitici con i mezzi della geometria. Così, per es., il problema di determinare il punto comune a due rette del piano equivale a quello di determinare la soluzione di un sistema di due equazioni lineari in due incognite. Lo scopo della g. analitica si raggiunge con l’introduzione di un sistema di coordinate (per cui essa prende anche il nome di metodo delle coordinate, o, dal nome del suo ideatore, metodo di Cartesio), cioè associando a ciascun ente geometrico di una certa famiglia un insieme ordinato di numeri, che siano individuati da quell’ente e che a loro volta lo individuino. Per es., un punto in un piano è individuato da due numeri, le sue distanze da due rette ortogonali prefissate (coordinate cartesiane nel piano). La suddivisione usuale della g. analitica è la seguente: g. sulla retta, g. nel piano, g. nello spazio e negli iperspazi. Gli argomenti tradizionali della g. analitica piana sono: proprietà proiettive, proprietà affini, proprietà metriche del piano e delle curve (algebriche o no), e in particolare la teoria delle coniche; nello spazio, proprietà proiettive, affini, metriche dello spazio e delle curve e superfici, e in particolare la teoria delle quadriche e delle superfici rigate. G. combinatoria Assiomatizzazione della teoria delle matroidi (➔).

G. del compasso Va sotto questo nome lo studio dei problemi e delle costruzioni che si possono risolvere mediante l’uso del solo compasso. È da notare la proprietà: ogni problema geometrico risolubile con la riga e con il compasso è risolubile anche con il solo compasso (G. Mohr, L. Mascheroni). G. descrittiva È quella parte della g. che ha per scopo la rappresentazione delle figure spaziali mediante figure di un certo piano detto quadro (o, in casi particolari, mediante figure di una prefissata superficie), in modo che dall’immagine della figura (e, s’intende, dalla conoscenza della legge di rappresentazione) si possa ricostruire la figura spaziale. Ogni insieme di regole che permetta di realizzare tale rappresentazione costituisce un metodo della g. descrittiva. I metodi più usati sono: a) metodo di Monge, o della doppia proiezione ortogonale, che consiste nel proiettare ortogonalmente la figura spaziale sopra due piani mutuamente ortogonali, e nel ribaltare poi l’un piano sull’altro; b) metodo dell’assonometria, che consiste nel proiettare ortogonalmente la figura spaziale sopra tre piani mutuamente ortogonali e nel proiettare poi tali tre proiezioni e la stessa figura spaziale sopra il quadro da un centro di proiezione improprio; c) metodo della proiezione centrale e metodo della prospettiva, che consistono nel proiettare la figura spaziale sopra il piano rappresentativo da un centro di proiezione proprio; d) metodo delle proiezioni quotate, che consiste nel proiettare ortogonalmente la figura spaziale sopra un piano e nell’associare a ogni punto-proiezione un numero, indicante la distanza dal piano del punto obiettivo; e) ciclografia, in cui ogni punto è rappresentato da un cerchio orientato avente per centro la proiezione ortogonale del punto sopra il piano rappresentativo e per raggio la distanza del punto dal piano. Poiché sostanzialmente il mezzo con il quale si realizzano i metodi della g. descrittiva è quello di proiettare la figura in uno o più modi, essi si chiamano anche metodi di proiezione (➔).

In ciascuno dei metodi della g. descrittiva, assegnata la legge di rappresentazione, per poterlo utilmente applicare è opportuno determinare in quali relazioni si traducano le condizioni di appartenenza, di parallelismo, di ortogonalità, come si risolvano le questioni metriche (misure di distanze e angoli, ribaltamenti), i problemi elementari (per es., data la rappresentazione di tre punti non allineati, determinare la rappresentazione del piano che li contiene) ecc. La g. descrittiva permette quindi di sostituire la considerazione di ogni figura spaziale con quella della corrispondente figura piana, e quindi di risolvere problemi spaziali mediante costruzioni piane. Tra le applicazioni tecniche della g. descrittiva ricordiamo la rappresentazione delle superfici topografiche, la teoria delle ombre e del chiaroscuro, la fotogrammetria, la stereotomia o taglio delle pietre. G. differenziale È lo studio ‘in piccolo’ degli enti geometrici, cioè lo studio delle proprietà degli intorni di un punto, le quali rimangono invariate di fronte ai movimenti (g. differenziale metrica) o alle omografie (g. differenziale proiettiva). Sono, per es., concetti di g. differenziale proiettiva: la tangente a una curva, il piano osculatore a una curva sghemba, il piano tangente a una superficie ecc. Sono concetti di g. differenziale metrica: la normale a una curva piana, il triedro fondamentale, la curvatura e la torsione di una curva sghemba, la curvatura gaussiana e media di una superficie ecc. In tal senso si parla, più propriamente, di g. differenziale in piccolo, in contrapposto alla g. differenziale in grande o globale che consiste invece nello studio delle proprietà differenziali di un dato ente (curva, superficie ecc.) le quali implicano la considerazione dell’ente stesso nella sua integrità, senza limitarsi quindi all’intorno di un punto. Per es., la nozione di ‘vertice’ di una curva piana C (punto in cui C ha un contatto di ordine ≥3 con il suo cerchio osculatore) appartiene alla g. differenziale locale, mentre appartiene alla g. differenziale globale il teorema che «ogni ovale (curva chiusa convessa) ha almeno quattro vertici» (come accade per l’ellisse).

Quantunque le origini storiche della g. differenziale si possano far risalire alle origini del calcolo differenziale, del quale essa utilizza i metodi, e quantunque siano da segnalare risultati di rilievo nel 18° sec. (si ricordi, per es., il teorema di Eulero sulla curvatura delle superfici), è però necessario giungere fino a Gauss e Riemann, nel 19° sec., per poter parlare della g. differenziale in senso moderno. L’opera di Gauss apre infatti un nuovo capitolo nello studio di una superficie, con l’introduzione di alcuni concetti fondamentali e con l’uso sistematico di nuovi strumenti rivelatisi assai fecondi. L’idea che sta alla base della teoria gaussiana consiste anzitutto nel riferire i punti della superficie a un sistema di due coordinate u, v (coordinate gaussiane, analoghe alle ordinarie coordinate cartesiane x, y nel piano), e nel far discendere le proprietà metriche intrinseche della superficie (come distanze, angoli, aree sulla superficie, curvatura gaussiana della stessa ecc.) da una forma differenziale quadratica, definita positiva, nelle u, v, del tipo:

ds²=Edu²+2Fdudv+Gdv²

in cui E, F, G sono convenienti funzioni del punto (u, v). Il ds² ora scritto non è altro che il quadrato dell’elemento d’arco di una linea tracciata sulla superficie, ovvero, come si suol dire, è pari alla distanza tra due punti infinitamente vicini della superficie (➔ superficie). Abbiamo parlato di proprietà intrinseche, in quanto si tratta di proprietà che rimangono invariate comunque si deformi la superficie quando la si pensi realizzata mediante un sottilissimo velo flessibile e inestensibile, senza produrre in essa strappi o duplicature.

fig. 1

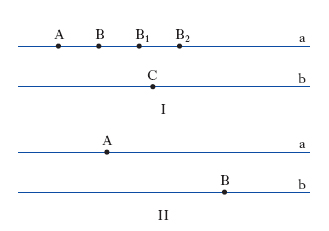
Notevole sviluppo ha avuto la g. differenziale stocastica che, sorta inizialmente in tre contesti differenti ma correlati, ha assunto un ruolo autonomo nella matematica e studia equazioni stocastiche (➔ equazione) su varietà differenziabili. G. euclidea La g. del piano e dello spazio il cui contenuto e i cui metodi sono modellati direttamente sugli Elementi di Euclide; si può identificare con la g. elementare sviluppata secondo il metodo euclideo. G. dei frattali Costituisce un nuovo campo di indagine per lo studio di particolari configurazioni geometriche derivanti dall’uso della grafica al computer, ma rispondenti a precise costruzioni matematiche. G. intrinseca Relativamente a un dato ente, è la g. che si può costruire sopra quell’ente pensato a sé stante e a prescindere dall’ambiente in cui è o può essere immerso. Esempi di g. intrinseca sono: la g. metrica costruita su una varietà riemanniana in base al concetto di metrica riemanniana. G. non archimedea G. in cui non vale il postulato di continuità secondo Archimede, cioè: dati due segmenti, può non esistere un multiplo del più piccolo che sia maggiore del più grande; possono tuttavia valere postulati di continuità in altra forma (per es., quella di Cantor). Un esempio di continuo non archimedeo è il seguente (fig. 1): fissate due rette orizzontali a, b, si ordinino i loro punti in modo che se A, B stanno sulla stessa retta, sia seguente il punto che sta più a destra; se A, B stanno su rette diverse sia seguente quello che sta sulla seconda; si chiami segmento AB l’insieme dei punti che seguono A e precedono B; se ora A, B, C sono tre punti presi, nell’ordine: A e B sopra a e C sopra b, nessuno dei successivi multipli AB₁, AB₂ ecc. di AB può superare AC, e dunque non vale il postulato di Archimede. Continua tuttavia a valere il postulato di Cantor (ma non quello di Dedekind).

fig. 2

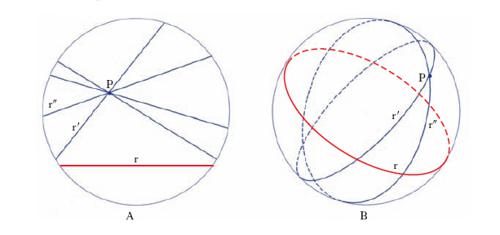
G. non euclidea G. nella quale non vale il 5° postulato di Euclide, o postulato delle parallele (per un punto esterno a una retta passa una e una sola parallela a una retta data; fig. 2). Tale g. è in altre parole un sistema ipotetico-deduttivo costruito in base ai postulati della g. euclidea a esclusione del 5°. Naturalmente non esiste un’immagine concreta della g. non euclidea costruita con enti geometrici considerati nel senso intuitivo della parola, e anzi taluni teoremi sembrano in contrasto con l’intuizione (per es., la somma degli angoli interni di un triangolo è sempre diversa da due angoli retti e non è costante per tutti i triangoli); s’intende che non sono però in contraddizione, dal punto di vista logico, con i postulati. Esistono due tipi di g. non euclidea, la g. iperbolica o di Lobačevskij, nella quale si postula che da ogni punto escono due parallele a una retta data, e la g. ellittica o di Riemann, nella quale si postula la non esistenza di parallele. Come caso limite di entrambe si ha la g. parabolica, che è la g. euclidea. Si deve a E. Beltrami la costruzione di un modello della g. iperbolica piana, nell’ordinario spazio a tre dimensioni, e precisamente sulla superficie della pseudosfera, rappresentando i punti del piano nei punti della pseudosfera e le rette del piano nelle geodetiche della stessa superficie. La costruzione di un modello siffatto è molto importante anche dal punto di vista logico, poiché la sua esistenza dimostra l’assenza di contraddizioni nei postulati e quindi dà piena validità alla costruzione geometrica fatta per via ipotetico-deduttiva. Si conoscono anche altri modelli, costruiti per es., nell’ambito della g. proiettiva, della g. iperbolica, della g. ellittica.

G. numerativa È quella teoria matematica, in certo senso facente parte della g. algebrica, la quale si occupa della determinazione a priori del numero delle soluzioni di un problema di carattere algebrico. Nella g. numerativa prevalgono due indirizzi: quello numerativo, che si occupa solo della determinazione di caratteri numerici, e quello funzionale, che si occupa anche dell’intimo significato di tali numeri.

G. proiettiva È l’insieme delle proprietà delle figure degli spazi proiettivi, che sono invarianti rispetto alle proiettività, cioè alle trasformazioni direttamente legate alle operazioni di proiezione e sezione; dal punto di vista di Klein la g. proiettiva ha dunque come gruppo fondamentale il gruppo delle proiettività. Le figure, o forme, fondamentali della g. proiettiva (piana o spaziale) sono: forme di prima specie (retta punteggiata, fascio di rette, fascio di piani); forme di seconda specie (piano punteggiato, piano rigato, stella di rette, stella di piani); forme di terza specie (spazio punteggiato, spazio di piani) ecc.; si vede subito che le operazioni di proiezione e sezione mutano ciascuna forma in una forma della stessa specie. Il concetto basilare della g. proiettiva è quello di birapporto di quattro elementi di una forma di prima specie, in quanto esso è il primo invariante proiettivo. Sono argomenti di studio di tale g. la teoria delle proiettività e delle omografie, la teoria della polarità e dei sistemi nulli, la generazione proiettiva di curve e superfici ecc. Se le origini della g. proiettiva si possono far risalire agli studi di prospettiva degli artisti del Rinascimento, la sua sistemazione come disciplina scientifica si ha soltanto con J.-V. Poncelet e con K.G.C. Staudt; quest’ultimo, in particolare, ne ha dato una costruzione di notevole perfezione ed eleganza. Verso la fine del 19° sec. la g. proiettiva non sfuggì all’analisi dei fondamenti della g. e della intera matematica; venne così messa in luce la possibilità di presentare la g. proiettiva come un sistema ipotetico-deduttivo che poggia su tre tipi di postulati: 1) postulati di appartenenza; 2) postulati di ordine; 3) postulati di continuità. Venne così anche messa in maggiore evidenza la legge di dualità della g. proiettiva, già rilevata esplicitamente da J.-D. Gergonne e da Poncelet. G. riemanniana Impostazione della g. differenziale secondo Riemann. Si pensi di individuare i punti di una varietà a r dimensioni mediante certe coordinate (x₁, x₂, ..., x_r), e si introduca la forma differenziale quadratica, definita positiva,

i cui coefficienti a_ij sono convenienti funzioni del punto (x₁, ..., x_r). Con Riemann, si può assumere il ds² ora scritto come quadrato della distanza tra due punti infinitamente vicini (x₁, ..., x_r) e (x₁+dx₁, ..., x_r+dx_r) introducendo così una ‘metrica’ nella varietà, che prende il nome di varietà riemanniana. A partire dall’espressione del ds² è possibile definire l’angolo di due curve in un loro punto comune, la distanza tra due punti A e B della varietà, le curve geodetiche ecc. Tutte le proprietà della varietà che discendono dalla metrica, cioè dal ds², costituiscono la g. riemanniana della varietà stessa; questa g. studia dunque le proprietà metriche spettanti alla varietà in sé stessa, indipendenti dall’eventuale immersione in un certo spazio ambiente, e in questo senso si parla anche di g. metrica intrinseca. Lo spazio euclideo a r dimensioni rientra come caso particolarissimo tra le varietà riemanniane. Viceversa una varietà riemanniana è di tipo euclideo se in essa, relativamente a un opportuno sistema di coordinate, il ds² si riduce alla cosiddetta ‘forma pitagorica’, cioè alla forma ds²=dx₁²+dx₂²+ ... +dx_r², e la metrica della varietà si riduce perciò alla ordinaria metrica euclidea. In ogni caso la g. della varietà è una g. non di tipo euclideo. La condizione affinché la metrica possa ricondursi alla forma pitagorica è data dall’annullarsi del ‘tensore di Riemann’; questo permette di calcolare certe ‘curvature’, che sono tutte nulle nel caso di uno spazio euclideo, mentre in generale danno una misura di quanto la varietà riemanniana e la relativa g. si discostino dall’ordinario spazio euclideo e relativa g. (➔ anche tensore).

G. e fisica

Tra i tanti importanti risultati classici ritrovati in modo rigoroso con i metodi moderni e le nuove possibilità che questi hanno aperto all’indagine dei geometri, è opportuno segnalare che dagli ultimi anni del 20° sec. nuove idee, provenienti dalla fisica, hanno cominciato a far luce su alcuni problemi classici insoluti, che neanche i nuovi metodi erano riusciti a scalfire. Queste nuove idee si possono compendiare in quelle, fra loro correlate, di simmetria speculare (mirror symmetry) e di coomologia quantica (quantum cohomology), motivate da teorie fisiche quali la teoria delle stringhe e la teoria quantistica dei campi. La teoria delle superstringhe suggerisce che la parte compatta della varietà spazio-tempo sia una varietà compatta complessa liscia X, di dimensione tre, tale che la classe canonica K_X sia banale. Queste varietà si dicono varietà di Calabi-Yau, e la loro completa classificazione e descrizione rappresenta un problema aperto in g. algebrica. I problemi numerativi nascono dalla constatazione che, in generale, su una siffatta varietà X vi è soltanto un numero finito di curve razionali con data classe di omologia, e dunque si pone la questione di contare il numero di tali curve, questione che ha interesse fisico. Il primo problema di questo tipo fu affrontato classicamente da H. Schubert nel 1879, il quale contò in 2875 il numero delle rette che appartengono a un’ipersuperficie quintica (di quinto grado) generale di P⁴, che è appunto il più semplice esempio di varietà tridimensionale di Calabi-Yau. La soluzione del problema generale di contare il numero delle curve razionali di dato grado su un’ipersuperficie quintica generale di P⁴, suggerita dall’idea fisica dell’esistenza della simmetria speculare, è stata ottenuta nel 1995 da M. Kontsevich. Un problema analogo è quello del calcolo del numero delle curve razionali di dato grado d del piano passanti per 3d-1 punti generali dello stesso piano: infatti, è facile verificare che tali curve dipendono da 3d-1 parametri e quindi ne passa un numero finito per 3d-1 punti sufficientemente generali. Anche tale questione è stata risolta, da Kontsevich e J. Manin (1994), usando la coomologia quantica. In sostanza si definisce, per certe varietà come il piano, un anello di coomologia più generale di quello usuale, nel quale la moltiplicazione conserva traccia dei numeri di curve razionali che verificano certe proprietà quali, per il piano, il passaggio per un dato numero di punti ecc. Questo nuovo anello risulta essere associativo, e l’associatività produce delle formule ricorsive per il calcolo delle curve razionali in questione. Vanno ancora citati alcuni sviluppi sulle singolarità. A.J. De Jong (nel 1995) ha dimostrato che, data una varietà proiettiva X definita su un campo qualunque k, ne esiste un’alterazione (X′, f), cioè esistono una varietà proiettiva liscia X′ definita sullo stesso campo k e un morfismo suriettivo f:X″→X. Un’alterazione è meno di una risoluzione delle singolarità, ma ha il pregio di esistere anche se k ha caratteristica positiva e, per molte questioni, può di fatto sostituire la risoluzione. È notevole che la dimostrazione di De Jong utilizzi in modo assai innovativo, nello studio delle singolarità, l’esistenza dello spazio dei moduli delle curve stabili. In ambito diverso, importante è stata anche la dimostrazione, data da K.S. Donaldson, della complessità degli spazi euclidei quadridimensionali, complessità che li distingue dagli spazi euclidei in altre dimensioni, e la dimostrazione, data da M.H. Freedman, della congettura di Poincaré (➔ Perelman, Grigori; Poincaré, Jules-Henri).