proiezione
Matematica
In geometria, la p. di un punto P da un centro S è l’operazione di tracciare la retta SP; p. di una retta r da un centro S è la costruzione del piano individuato da r e S; p. di un punto P da una retta s è la costruzione del piano individuato da s e P; p. di una linea λ da un centro S è la p. da S dei singoli punti di λ, cioè la costruzione del cono di vertice S e direttrice λ. In generale, si chiama poi p. di una figura F su una figura F′ l’operazione che consiste nel congiungere i singoli punti di F con il centro di p. e intersecare con F′ ciascuna delle rette così ottenute. P. assiale La p. eseguita proiettando da una retta. P. centrale La p. eseguita proiettando da un punto proprio. P. ortogonale sopra un piano La p. eseguita dal punto all’infinito in direzione ortogonale al piano; p. ortogonale sopra una retta è la p. eseguita dalla retta all’infinito corrispondente alla giacitura ortogonale alla retta data. P. parallela La p. eseguita proiettando da un punto improprio. P. stereografica La p. di una quadrica da un suo punto sopra un piano.
Scopo della geometria descrittiva è quello di rappresentare le figure spaziali sopra un piano in modo che dalla rappresentazione piana e dalla conoscenza della legge di rappresentazione si possa risalire alla figura spaziale. L’equivalenza tra la figura spaziale e la sua rappresentazione piana permette quindi non solo di rappresentare le figure, ma anche di risolvere graficamente, mediante sole costruzioni piane, problemi di geometria spaziale. Ciascuno dei sistemi di regole che permettono la rappresentazione piana costituisce un metodo della geometria descrittiva, detto anche metodo di proiezione.
Metodo delle p. ortogonali (o di Monge)
Elementi di riferimento sono due piani π1 (di regola orizzontale) e π2 (di regola verticale), detti rispettivamente primo e secondo quadro, mutuamente ortogonali; la loro intersezione si dice linea di terra e si indica con LT; nel piano rappresentativo si traccerà la LT, con la convenzione che tale piano coincida con uno dei quadri e che l’altro passi per la LT e sia ortogonale al primo.
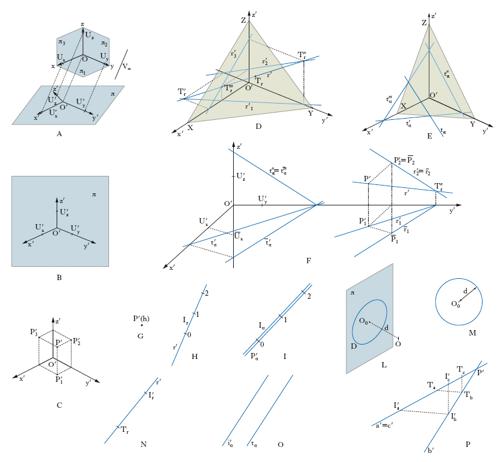
Legge di rappresentazione: un generico punto P dello spazio si rappresenta mediante le sue due p. P1, P2, che si ottengono proiettando ortogonalmente il punto sui due quadri e poi ribaltando l’uno sull’altro, di modo che P1 e P2 vengano a trovarsi sopra una retta perpendicolare alla LT, che è chiamata linea di richiamo (fig. 1A, B). Una retta r in posizione generica si rappresenta in due modi; il primo, mediante le sue p. r1, r2, che si ottengono proiettando ortogonalmente la retta sopra i due quadri e poi ribaltando l’uno sull’altro come nella rappresentazione del punto; il secondo mediante le sue tracce, cioè i suoi punti d’incontro con i due quadri, riportati, al solito, in un medesimo piano mediante ribaltamento in modo da ottenere i punti T′r, T″r (fig. 1C, D); la fig. 1D mette altresì in evidenza la semplice costruzione che permette di passare dalle p. alle tracce e viceversa. Un piano α in posizione generica si rappresenta mediante le sue tracce, cioè le sue rette d’incontro con i quadri, riportate mediante ribaltamento sullo stesso piano; si ottengono così due rette t′α, t″α che s’intersecano sulla LT (fig. 1E, F). Particolari accorgimenti richiede la rappresentazione di elementi in posizione eccezionale, quali per es.: le rette di profilo, cioè ortogonali alla LT (fig. 1G), le rette orizzontali, cioè parallele a π1 (fig. 1H), le rette di fronte, cioè parallele a π2 (fig. 1I), i piani proiettanti in prima p., cioè perpendicolari a π1 (fig. 1L), o in seconda p., cioè perpendicolari a π2 (fig. 1M), i piani di profilo, cioè perpendicolari alla LT (fig. 1N).
Molte volte, per facilitare talune costruzioni si completa la rappresentazione mediante una terza p., che si ottiene fissando un piano di profilo π3; per ottenere le terze p. si proiettano ortogonalmente gli elementi (punti o rette) su π3 oppure si intersecano con esso per ottenere le terze tracce (per le rette i piani); in ogni caso si riporta il risultato sul quadro mediante un ribaltamento; in fig. 1O è schematizzato il procedimento spaziale; nella fig. 1P è la costruzione piana che permette di costruire la terza p. di un punto, a partire dalla prima e dalla seconda p. del punto stesso.
Metodo dell’assonometria (o della p. assonometrica)
È detto anche, con termine improprio, prospettiva assonometrica. Elementi di riferimento sono: una terna trirettangola monometrica Oxyz, della quale si indicano con Ux, Uy, Uz i punti unità sugli assi e con π1, π2, π3 i piani xy, yz, zx rispettivamente; il quadro π; la direzione di assonometria V∞, cioè un punto improprio in direzione non parallela al quadro (fig. 2A, ove la terna Oxyz è terna di riferimento nello spazio). La rappresentazione di tali elementi si ottiene proiettando la terna da V∞ su π; la rappresentazione in tal modo ottenuta è del tipo della fig. 2B, la quale, grazie al teorema di K.W. Pohlke, permette di risalire agli elementi nello spazio. Talvolta si aggiunge, nel riferimento, il triangolo fondamentale, cioè il triangolo che ha per vertici i punti d’incontro X, Y, Z degli assi x, y, z con il quadro π.
Legge di rappresentazione: un punto P dello spazio si rappresenta proiettandolo anzitutto ortogonalmente sui piani π1, π2, π3, in modo da ottenere i punti P1, P2, P3; quindi si proiettano i quattro punti P, P1, P2, P3 da V∞ su π, ottenendo i quattro punti P′ (p. assonometrica vera di P), P′1, P′2, P′3 (prima, seconda, terza p. assonometrica di P), che costituiscono la rappresentazione di P; questi quattro punti sono legati da relazioni grafiche espresse in fig. 2C dalle linee tratteggiate. Una retta r si rappresenta (fig. 2D), in maniera del tutto analoga, mediante le quattro proiezioni r′, r′1, r′2, r′3; oppure si interseca con i tre quadri π1, π2, π3 e si proiettano poi tali intersezioni da V∞ su π; si ottengono così i punti T′r, T″r, T‴r (prima, seconda, terza traccia della r); le relazioni grafiche tra gli elementi considerati sono messe in luce dalle linee tratteggiate. È da osservare che agli effetti della rappresentazione della retta è sufficiente assegnare due delle p. oppure due delle tracce. Un piano α si rappresenta mediante le sue tracce t′α, t″α, t‴α (che si intersecano a due a due sugli assi, come in fig. 2E), definite analogamente alle tracce di una retta; due di esse sono sufficienti per rappresentare completamente il piano. Quando sia dato il triangolo fondamentale, la rappresentazione della retta o del piano si completa con la traccia vera, che è l’intersezione Tr della retta r con π o, rispettivamente, l’intersezione tα del piano α con π; per la loro costruzione fig. 2D, E.
Assonometria cavaliera è quella nella quale il quadro π è coincidente (o, più in generale, parallelo) a uno dei piani cartesiani, normalmente al piano π2; in usi particolari (assonometria militare) si ha che π è coincidente (o parallelo) con π1. In entrambi i casi è immediato il passaggio dalla rappresentazione assonometrica alla rappresentazione mongiana associata, cioè alla rappresentazione mongiana per la quale i due quadri coincidono con i piani π1, π2 di riferimento dell’assonometria. Il passaggio si opera in base alle seguenti regole, che enunciamo per l’assonometria cavaliera: a) seconda p. assonometrica e seconda p. di Monge coincidono; b) tra la prima p. assonometrica e la prima p. di Monge intercorre un’affinità (in generale obliqua) avente per asse l’asse y′ e nella quale si corrispondono il punto U′x (fig. 2F) e il punto Ūx ottenuto riportando sull’asse z′, a partire da O′, nel verso discorde a z′, il segmento O′ U′x = O′U′y = O′U′z; nella stessa fig. 2F è eseguita la costruzione per un punto P, una retta r e un piano α; le rappresentazioni mongiane sono indicate mediante sopralineatura.
Assonometria ortogonale è quella nella quale la direzione di assonometria V∞ è ortogonale al quadro di modo che la p. assonometrica vera è una p. ortogonale. Secondo che coincidano tutte e tre, due o nessuna delle unità assonometriche sugli assi, si parla rispettivamente di assonometria isometrica (monometrica), dimetrica o trimetrica.
Prendendo un riferimento mongiano nel quale il primo quadro coincida con il quadro π dell’assonometria e il secondo quadro sia ortogonale a questo e passi per una linea di terra LT, assegnata in π, il passaggio dalla rappresentazione assonometrica alla mongiana si esegue in base a costruzioni abbastanza semplici.
Metodo delle p. quotate (o del piano quotato)
Elementi di riferimento sono un piano π, che funge da quadro e che abitualmente si pensa orizzontale, e un’unità di misura u.
Legge di rappresentazione: un punto P si rappresenta con la sua p. ortogonale P′ sul quadro e con la sua quota, vale a dire indicando la misura con segno, h, del segmento orientato P′P rispetto all’unità di misura u (fig. 2G). Una retta generica r si rappresenta con la sua p. graduata, cioè mediante la sua p. ortogonale r′ su π, sulla quale sono segnate le p. dei punti della retta aventi quota, cioè distanza da π, eguale a u, 2u, … . Il segmento grafico determinato da due successive di queste p. si chiama intervallo della retta e si denota con Ir (fig. 2H). Un piano generico α si rappresenta prendendo una sua retta di massima pendenza, cioè una retta pα, appartenente al piano α e perpendicolare all’intersezione di α con π, e rappresentando poi questa retta come detto sopra; per distinguere tale rappresentazione da quella di una retta, si suole indicarla materialmente mediante due tratti molto vicini; il suo intervallo (intervallo del piano) si indica con Iα (fig. 2I).
Metodo della p. centrale
Elementi di riferimento sono un quadro π e un centro di vista O, cioè un punto proprio non appartenente a π (fig. 2L). Essi si rappresentano mediante il punto principale O0 (p. ortogonale di O su π) e il cerchio di distanza D (cerchio tracciato su π, di centro O0 e avente per raggio la distanza principale d, cioè il segmento O0O; fig. 2M).
Legge di rappresentazione: una retta generica r si rappresenta (fig. 2N) mediante la sua traccia Tr (punto d’incontro di r con π) e la sua fuga I′r (punto d’incontro con π della parallela a r per O); la p. r′ di r da O su π è la retta TrI′r. Un piano generico α si rappresenta (fig. 2O) mediante la sua traccia tα (retta d’incontro di α con π) e la sua fuga i′α (retta d’incontro di π con il piano parallelo ad α per O). Un punto P si rappresenta (fig. 2P) mediante la sua p. P′ da O su π e mediante una retta generica a per P (rappresentata a sua volta mediante traccia e fuga); un punto ammette quindi infinite rappresentazioni; si passa dall’una all’altra tenendo presente che se due rette a, b passano per P, le loro immagini a′, b′ passano per P′ e le rette TaTb, I′aI′b sono parallele tra loro. In fig. 2P sono date tre rappresentazioni del punto P, mediante le rette a, b, c.
Per il metodo della prospettiva ➔ prospettiva.
Medicina
In neuroanatomia, fibre di p., quelle che collegano le parti del cervello fra loro e col midollo spinale; conducono le correnti attive solo in una direzione, dal centro verso la periferia o viceversa (per es., il fascio piramidale, quello spino-talamico e le vie talamo-corticali). Le aree di p. sono costituite dai centri corticali, in cui iniziano e terminano le fibre di proiezione.
Psicologia
In psicanalisi, processo difensivo per il quale il soggetto attribuisce a persone o cose sentimenti, desideri e aspetti propri che rifiuta di riconoscere in sé stesso. La p. si presenta regolarmente nel corso del trattamento psicanalitico e nel transfert.