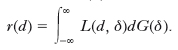stima

stima Valutazione approssimata del valore di un bene o una grandezza.

Economia

Valutazione monetaria di qualsiasi fatto che costituisca un aspetto o una conseguenza di carattere economico.

Sono dette, complessivamente, operazioni di s. o estimali le operazioni catastali di natura tecnico-economica (classificazione, qualificazione, classamento e formazione delle tariffe d’estimo; ➔ catasto) con cui si arriva ad accertare il reddito delle singole particelle catastali. Per alcuni terreni (pascoli e gerbidi, orti e frutteti per i quali sia difficile determinare il prodotto, stagni e laghi da pesca), il cui classamento presenta gravi problemi, si ricorre a s. diretta, e per quelli non adibiti all’ordinaria coltura, come ville, giardini e simili, a s. per parificazione, valutandone il reddito presuntivo in base al prodotto dei migliori terreni vicini.

Matematica

In statistica, l’analisi delle procedure che determinano la s. dei parametri. È un importante capitolo della teoria dei campioni statistici (➔ campione). Si distinguono due diversi metodi di s.: puntuale e per intervalli (o per regioni).

La s. puntuale consiste nel definire in corrispondenza di ogni parametro da stimare un solo valore, funzione dei dati campione. Per la scelta di tale funzione si può seguire l’impostazione di T. Bayes o un’impostazione oggettivistica. Secondo l’impostazione bayesiana, se δ è il parametro da stimare, e se per il campione osservato la sua funzione di ripartizione a posteriori è G(δ) (➔ ipotesi), data una funzione di perdita L(d, δ), la quale misura il danno che si subisce stimando δ con d, la s. bayesiana di δ è il valore di d che minimizza il valor medio di L(d, δ), valor medio dato dalla seguente funzione di rischio r(d):

Se, per es., L(d, δ)=(d−δ)2, la s. bayesiana di δ è la media della distribuzione a posteriori, se L(d, δ)=∣d−δ∣, la s. è data dalla mediana della stessa distribuzione. L’impostazione oggettivistica prescinde dalla distribuzione a priori di δ, che è invece richiesta dalla teoria bayesiana e senza la quale la distribuzione a posteriori non è determinabile, e si fonda pertanto sulla funzione di verosimiglianza p(x, δ) e sulle distribuzioni dei parametri campione che da essa si ricavano. Una s. d è detta corretta se il suo valor medio è uguale a δ, cioè se E(d)=δ. Una s. d è detta consistente (nell’estrazione bernoulliana) se converge in probabilità a δ quando N → ∞, dove N denota la dimensione del campione; condizione sufficiente perché ciò avvenga è che si abbia: limn→∞ E[(d−δ)2]=0. La varianza del campione, per es., è una s. consistente della varianza della popolazione. Se d è una s. corretta di δ con varianza finita e tale che nessun’altra s. corretta abbia varianza minore, d è detta s. efficiente di δ. Una s. in cui è concentrata tutta l’informazione che si possa trarre dal campione circa il parametro da stimare è detta sufficiente. Un metodo che consente di individuare s. utili è quello della massima verosimiglianza. Il metodo consiste nell’assumere come s. di d il valore che rende massima la funzione di verosimiglianza p(x, δ). Sotto ipotesi poco restrittive, tali s. godono di alcune importanti proprietà: sono consistenti, asintoticamente efficienti e tendono a distribuirsi normalmente al crescere di N. Applicando questo metodo si trovano, per es., la media e la varianza campionaria come s. per i corrispondenti parametri di una popolazione normale.

Le s. per intervalli presentano dei vantaggi rispetto alle s. puntuali che sono, nella quasi totalità dei casi, in maggior o minor misura, errate. Il metodo consiste nel determinare, in base alle osservazioni, un intervallo, detto intervallo di confidenza, secondo un procedimento tale che, eseguendo l’operazione su tutti i campioni di un universo, gli intervalli coprano il vero valore della caratteristica da stimare con una frequenza prefissata, frequenza che è detta coefficiente di confidenza. In generale (ma non sempre) il punto centrale dell’intervallo di confidenza è costituito da una s. puntuale corretta con varianza piccola; l’ampiezza media dell’intervallo, infatti, cresce al crescere della varianza e ovviamente gli intervalli sono tanto più utili quanto più sono piccoli. Se, per es., il campione proviene da una popolazione normale con varianza nota, σ2, fissato il coefficiente 1−α conviene usare l’intervallo avente gli estremi nei punti x̄−tα/2σ/√‾‾‾N e x̄+tα/2σ/√‾‾‾N per stimare la media della popolazione, essendosi indicato con x̄ la media del campione e con tα/2 il punto nel quale la funzione di ripartizione della variabile normale standardizzata assume il valore 1−α/2. Se invece si centrassero gli intervalli sulla mediana anziché sulle media del campione, la loro ampiezza risulterebbe maggiore, sebbene anche la mediana sia una s. corretta della media di una popolazione normale (e, più in generale, di qualunque popolazione simmetrica), perché la varianza della mediana campionaria è maggiore di quella della media.

I concetti su cui si fonda la moderna teoria degli intervalli di confidenza (dovuta a J. Neyman) possono essere così riassunti. Sia d una s. del parametro δ; si costruiscono due funzioni monotone e crescenti di δ, d′e d″ tali che per la probabilità condizionata a δ sia: P(d′<d<d″)=1−α. Indicate con δ′ e δ″ le funzioni inverse rispettivamente di d′ e d″ si ha allora anche: P(δ′<δ<δ″)=1−α e le variabili casuali δ′ e δ″ sono gli estremi degli intervalli di confidenza. In modo analogo si perviene alla costruzione di regioni di confidenza quando vi sono due o più parametri da stimare.

Trasporti

Nella navigazione marittima e aerea, s. della rotta, operazione che permette di determinare la rotta percorsa da una nave o da un aereo oppure il punto in cui il mobile si trova (punto stimato), eseguita in base a elementi ricavati sul mobile stesso, senza riferimenti né a terra né agli astri (➔ navigazione).