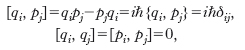quantizzazione

In fisica, proprietà di certe grandezze osservabili di poter assumere soltanto un certo insieme discreto di valori e anche il procedimento in base al quale si determinano questi valori. In elettronica e in tecnica delle telecomunicazioni, l’operazione, attuata con un quantizzatore, consistente nel suddividere il campo di variabilità di una grandezza continua in un numero finito di intervalli, in ciascuno dei quali la grandezza è sostituita con un valore rappresentativo (operazione che, insieme al campionamento, è fondamentale nella conversione analogico-digitale).

Nell’ambito della fisica classica i risultati possibili della misurazione di un’osservabile formano generalmente un insieme continuo. Nell’ambito della meccanica quantistica (➔ meccanica) ciò non avviene perché, mentre in alcuni casi le misure formano un insieme continuo, in altri esse formano un insieme discreto e in altri un insieme in parte discreto, in parte continuo. Un esempio della prima eventualità è fornito dalla posizione di una particella; un esempio della seconda eventualità è dato dal suo momento angolare orbitale, il cui quadrato può assumere solo i valori l(l+1)ℏ ², con ℏ costante di Planck ridotta e l intero positivo o nullo; un esempio dell’ultima eventualità è l’energia totale di un elettrone nel campo elettrico di un protone, che può avere tutti i valori positivi da 0 a ∞, ma solo un insieme discreto di valori negativi e cioè −13,6/n² eV, con n intero. Le varie possibilità elencate per le osservabili di un sistema si traducono, nel formalismo della meccanica quantistica, in cui a ogni osservabile è associato un operatore hermitiano che agisce nello spazio di Hilbert dei vettori di stato, in differenti proprietà dello spettro degli autovalori degli operatori che rappresentano quelle osservabili; tali proprietà sono legate alle relazioni di commutazione tra gli operatori stessi: le condizioni di q., nella usuale formulazione della meccanica quantistica, si riducono quindi a determinare tali relazioni.

Il procedimento che si segue, detto q. canonica, si fonda sull’analogia classica e richiede che il sistema che si vuole quantizzare sia descritto, classicamente, in forma hamiltoniana, cioè per mezzo di un appropriato numero di coordinate generalizzate, q_i, e dei corrispondenti momenti coniugati, p_i, con i=1,2, ..., N, essendo N il numero dei gradi di libertà del sistema (➔ meccanica). Il passaggio alla teoria quantistica si attua imponendo che le variabili canoniche q_i e p_i, per mezzo delle quali si possono esprimere tutte le altre variabili del sistema, considerate come operatori su uno spazio di Hilbert, abbiano i commutatori proporzionali alle rispettive parentesi di Poisson:

[1] formula

dove δ_ij è il simbolo di Kronecker e le graffe indicano le parentesi di Poisson tra le osservabili classiche; in questo modo, se la regola di q. è consistente, l’equazione di Heisenberg per qualunque osservabile riproduce l’equazione del moto classica per l’osservabile stessa. Dalle relazioni, dette relazioni di commutazione canoniche (o di Heisenberg), segue che variabili dinamiche classicamente indipendenti risultano quantisticamente compatibili e, inoltre, che, in una base in cui q_i è diagonale, è possibile porre p_i=−i ℏ/∂q_i (rappresentazione di Schrödinger). Si noti che se un’osservabile classica dipende dal prodotto di una funzione di q_i e di una funzione di p_i, a causa della non commutatività quantistica tra q_i e p_i, l’operatore da associare all’osserva­bile considerata non è univocamente de­finito: più di un operatore quantistico può essere associato alla stessa osservabile classica, dando luogo alle ambiguità di quantizzazione.