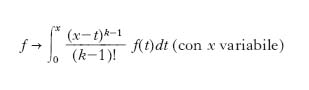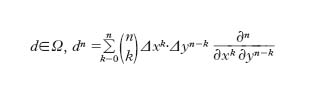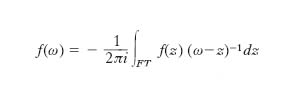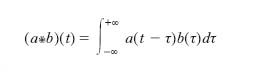operatore

Biologia

In genetica, tratto di DNA che fa parte di un operone e condiziona la trascrizione dei geni strutturali immediatamente adiacenti (➔ operone).

Filosofia

In filosofia analitica, un’espressione che serve a determinare un’altra espressione.

Economia

Persona che esegue per conto proprio o di terzi affari di banca o di borsa: o. di borsa, chi tratta affari nelle borse valori e nelle borse merci; o. di banca, funzionario della banca che esegue le operazioni di compravendita di titoli, cambi ecc., per ordine della clientela o della direzione della banca; o. in titoli, colui che tratta in borsa la compravendita dei soli titoli; o. principali, intermediari che effettuano in forma societaria, nel mercato telematico all’ingrosso, operazioni di compravendita su almeno 5 titoli emessi e garantiti dallo Stato.

Fisica

Ente matematico che si fa corrispondere a una determinata operazione o che si fa corrispondere a un’osservabile di un sistema fisico, cioè a una grandezza che si possa descrivere e misurare, in modo che l’applicazione di esso alla funzione di stato che descrive il sistema individui il valore aspettato dell’osservabile in questione.

Gli o. svolgono un ruolo fondamentale nella meccanica quantistica, nel cui schema teorico gli stati di un sistema sono rappresentati dai vettori di uno spazio di Hilbert ℋ e le sue variabili dinamiche da o. lineari in ℋ (➔ meccanica); in questo contesto, gli o. lineari più importanti sono quelli hermitiani e quelli unitari.

Dato l’o. A, il suo aggiunto, A⁺, è definito dalla relazione: (ϕ, A ψ)=(ψ, A⁺ ϕ)*, dove ϕ e ψ sono vettori di ℋ, (ϕ, Aψ) indica il prodotto scalare tra ϕ e il vettore Aψ, ottenuto dall’applicazione di A su ψ, e l’asterisco denota il complesso coniugato; se risulta A⁺=A, l’o. si dice hermitiano o, più propriamente, autoaggiunto. Con gli o. hermitiani si rappresentano le variabili dinamiche reali, e quindi le osservabili di un sistema fisico, giacché la quantità (ϕ, Aϕ), se A è hermitiano, risulta reale e può allora essere interpretata come valore d’aspettazione di un gran numero di misurazioni di un’osservabile, rappresentata da A, sullo stato fisico rappresentato dal vettore normalizzato ϕ (➔ osservabile).

Un o. U si dice unitario se il suo inverso coincide con l’aggiunto: UU⁺=I=U⁺U, dove I è l’o. identità; poiché gli o. unitari conservano il prodotto scalare tra i vettori, cioè si ha (Uϕ, Uψ)=(ϕ, ψ), e quindi sotto la loro azione restano inalterate le relazioni tra gli stati, con essi si rappresentano sia i cambiamenti di base in ℋ (➔ meccanica; rappresentazione), sia le corrispondenze tra le descrizioni dello stesso sistema dovute a osservatori che adottano differenti sistemi di riferimento (eventualmente relativi a gradi di libertà ‘interni’ come, per es., lo spin isotopico), quali sistemi di riferimento tra loro traslati, ruotati, con orientamento opposto degli assi coordinati, in moto relativo uno rispetto all’altro ecc.

Matematica

Il simbolo di un’operazione o, più in generale, di un’applicazione. Dato un insieme non vuoto A, si dice che ω è un o. unario (cioè applicabile a singoli termini) definito in A quando a ω è associata un’applicazione di A in A; in tale caso, dato un elemento x ∈ A, la sua immagine ottenuta applicando l’o. ω all’oggetto x si indica con ωx. Così, per es., possono considerarsi come o. unario il calcolo dell’opposto d’un numero, una omografia vettoriale e una funzione di una variabile a un solo valore.

La definizione data si generalizza pensando di associare a un o. ω un’applicazione del prodotto cartesiano A×A, ovvero di A×A×A, …, di Aⁿ, in A; in tal caso si dirà che ω è un o. binario, ternario, …, o n-ario, rispettivamente, definito in A; per es., il simbolo + si può considerare come un o. binario definito nell’insieme dei numeri reali R, se a esso si associa l’applicazione (x, y)→x+y (dove x, y ∈ R). Per omogeneità di nomenclatura si considera anche l’o. nullario (a zero termini) ω, al quale si associa semplicemente un elemento di A; ciò anche in analogia a quanto avviene nelle denominazioni delle operazioni.

Strutture di un insieme di operatori

Un insieme Ω di o. può essere dotato di una struttura dipendente dal modo con cui esso è stato definito, oppure indotta dalla struttura di cui si suppone dotato l’insieme A di oggetti nel quale sono definiti gli o. appartenenti a Ω, oppure anche indotta dalla struttura di cui eventualmente è dotato l’insieme B delle immagini (codominio), oppure infine dalle strutture di cui sono dotati il dominio A e il codominio B, nel qual caso si presenta il problema della compatibilità degli o. ω con tali strutture. Esaminiamo i vari casi, limitandoci, per semplicità, a considerare o. unari.

Sia Φ un insieme di o. definiti in un insieme A di oggetti. Definiamo l’insieme di o. Ω mediante le seguenti quattro regole: I) 1 ∈ Ω; II) Φ ⊂ Ω; III) se ω₁, ω₂ ∈ Ω, allora anche w₁ w₂ ∈ Ω; IV) con le regole I, II, e III si ottengono tutti gli elementi di Ω. A ciascun elemento di Ω associamo un’applicazione di A in A nel modo seguente: I′) a 1 associamo l’applicazione identica a → a (per ogni a ∈ A); II′) se ω ∈ Φ associamo a ω l’applicazione, già nota, a → ωa; III′) se ω₁, ω₂ ∈ Ω, associamo a ω₁ ω₂ l’applicazione a → ω₁ (ω₂a). Se a ogni elemento di Ω, in virtù delle I′, II′, III′, risulta associata una sola applicazione di A in A, Ω risulta essere un insieme di o. definiti in A, dotato della struttura di semigruppo con unità; l’o. ω₁ ω₂ si dice prodotto degli operatori ω₁ e ω₂ nell’ordine; questi si dicono permutabili qualora ω₁ ω₂=ω₂ ω₁; l’o. ω ω … ω (k volte) si indica anche con ω^k; per convenzione si pone ω⁰=1. Esempio: sia A l’insieme delle funzioni reali delle due variabili reali x e y, indefinitamente derivabili; sia Φ l’insieme {∂/∂x, ∂/∂y} (dove, per ogni f ∈ A, a ∂/∂x si associ l’applicazione f→∂f/∂x e a ∂/∂y l’applicazione f→∂f/∂y). L’insieme di o. Ω risulta dotato della struttura di semigruppo con unità, commutativo per il teorema di Schwarz; gli elementi di Ω sono ∂^h+k/∂x^h∂y^k (h, k=0, 1, 2, …).

Nella ulteriore ipotesi che, per ogni ω ∈ Φ, l’applicazione a→ω a (a ∈ A) sia biunivoca e aggiungendo la regola II bis): se ω ∈ Φ allora anche ω^–1 ∈ Ω si può dotare Ω della struttura di gruppo, in generale non abeliano. L’o. (ω^–1)^k si indica anche con ω^–k. Esempio: sia A l’insieme delle funzioni reali indefinitamente derivabili su tutto l’asse reale, nulle nell’origine con tutte le loro derivate; l’insieme Φ sia costituito dal solo elemento D, al quale si associa, per ogni f ∈ A, l’applicazione f→df/dx. L’insieme Ω risulta dotato della struttura di gruppo abeliano e i suoi elementi, a meno di eguaglianze, sono 1, D^k, D^–k (k=1, 2, …), dove all’o. D^k è associata l’applicazione f→d^kf/dx^k e all’o. D^–k l’applicazione

Siano A e B due insiemi muniti di un certo tipo di struttura e Φ un insieme di o. unari ω, τ, …, da A a B. Se R è una relazione binaria definita in B, si dice che si ha R(ω, τ) quando, per ogni a ∈ A, vale la relazione R (ωa, τa). Un o. ω si dice compatibile con tale tipo di struttura quando, per ogni a₁, a₂ ∈ A, si ha: I) da R (a₁, a₂) segue R (ωa₁, ωa₂); II) τ(ωa₁) =ω(τa₁). Esempi: la distributività di un o. è la sua compatibilità con la struttura di varietà lineare; la continuità è la sua compatibilità con la struttura di convergenza. Mettendo assieme più costruzioni del tipo precedente si potrà ottenere un insieme Ω di o. su cui istituire un vero e proprio calcolo operatorio. Per es., sia A l’insieme delle funzioni reali delle due variabili reali x e y, indefinitamente derivabili in tutto il piano e sia Φ l’insieme {∂/∂x, ∂/∂y}, dove a ∂/∂x si associ l’applicazione f→∂/∂x e a ∂/∂y l’applicazione f→∂f/∂y. Essendo A una varietà lineare sul corpo dei numeri reali, per quanto ora esposto, per il teorema di Schwarz e per la distributività della derivazione, Ω risulta un anello commutativo isomorfo all’anello dei polinomi in due indeterminate sul corpo dei numeri reali. Quindi, posto d=Δx∂/∂x+Δy∂/∂y (dove Δx,Δy ∈ R), si ha:

Tra gli elementi di Ω si trovano, per es., l’o. di Laplace: ∂²/∂x²+∂²/∂y², quello di d’Alembert: ∂²/∂x²−∂²/∂y² ecc.

Calcolo operatorio

Il calcolo operatorio e l’interesse allo studio degli o. come enti assoggettabili a una particolare algebra affiora, a partire dai lavori dei suoi fondatori, nelle maggiori questioni dell’analisi infinitesimale. Comunemente il calcolo operatorio veniva indicato anche come calcolo operatorio simbolico di O. Heaviside; questi, per primo, partendo da problemi sui circuiti elettrici trasformò le corrispondenti equazioni e sistemi differenziali in equazioni e sistemi algebrici, risolvendoli in maniera simbolica senza però il sostegno di un completo formalismo. Fondamentale il contributo di G. Giorgi per la sistemazione in una coerente teoria del calcolo con o. integrali. Gli sviluppi successivi hanno portato a una rigorosa definizione e specializzazione delle algebre degli operatori.

Lo studio degli o. lineari su spazi di Hilbert e delle algebre da essi generate è stato uno dei campi di ricerca più attivi negli anni 1990. Si sono infatti compresi molti legami con la topologia e la geometria differenziale: si sono sviluppati, in particolare, lo studio della geometria differenziale non commutativa, che è una generalizzazione del classico studio delle algebre di funzioni C^∞, e lo studio della teoria dei nodi topologici attraverso le C*-algebre, particolari algebre di Banach. Molto importanti, e dovute in larga parte alla scuola italiana (ricordiamo tra tutti S. Doplicher e R. Longo), sono anche le connessioni tra lo studio delle algebre di o. e la teoria dei campi quantistici.

Calcolo con o. lineari

Sia A un insieme di elementi che chiameremo vettori e K un corpo numerico, gli elementi del quale chiameremo scalari. Si dice che A è una varietà lineare sul corpo K quando: I) sia assegnato in A un vettore 0, detto vettore nullo; II) sia assegnata un’applicazione commutativa e associativa di A×A in A, detta somma; III) sia assegnata un’applicazione di K×A in A, distributiva in entrambi i sensi rispetto alla somma e associativa, detta prodotto; IV) si abbia 1∙a=a e 0∙a=0, per ogni a ∈ A. Supponiamo ora che siano date due varietà lineari A e B sullo stesso corpo numerico K: un o. unario ω da A a B si dice lineare se e solo se, per ogni k₁, k₂ ∈ K e a₁, a₂ ∈ A, si ha

ω(k₁a₁+k₂a₂)=k₁(ωa₁)+k₂(ωa₂).

Nel caso particolare che sia B=K, l’o. lineare da A in K si chiama di solito funzionale lineare di A. Esempio: l’insieme A delle funzioni reali di due variabili reali, indefinitamente derivabili in tutto il piano, è un esempio di varietà lineare sul corpo dei numeri reali.

Spesso la varietà lineare è anche compatibile con una struttura di convergenza; si parla allora di o. lineari continui. Siano assegnate due varietà lineari A e B, nelle quali siano state introdotte delle nozioni di convergenza e di limite (per successioni o, più in generale, per insiemi provvisti di un ordinamento filtrante): si dice che l’o. ω da A in B è continuo quando, ogni qual volta si verifichi l’eguaglianza a=lim_ia_i, vale di conseguenza l’eguaglianza ωa=lim_i (ωa_i), per a, a_i ∈ A e {a_i} successione o famiglia diretta di elementi. Queste nozioni di convergenza, limite e continuità consentono poi d’introdurre in modo naturale le altre due operazioni fondamentali dell’analisi matematica: la derivazione e l’integrazione, per o. dipendenti da un parametro variabile nel corpo K; così pure s’introduce in modo naturale la nozione di convergenza e di somma per una serie di o. lineari. Tra le varietà lineari in cui sia definita una nozione di convergenza e di limite, assai notevoli sono gli spazi di Banach, di Hilbert, per i quali ➔ spazio.

Di importanza fondamentale è il problema dell’inversione di un o. lineare, ossia quello di discutere l’equazione ωa=b nell’incognita a, da ricercare in una varietà lineare A, dove b è un assegnato vettore di una varietà lineare B, e ω è un assegnato o. lineare da A in B, mentre A e B sono lineari sullo stesso corpo. Un notevole risultato è il seguente: se A e B sono due spazi di Banach e ω è un o. lineare continuo da A in B univocamente invertibile, anche l’o. inverso ω^–1 è lineare e continuo. Grande importanza hanno pure i teoremi di rappresentazione, che permettono di dare definizioni costruttive per gli o. lineari continui da una varietà lineare in un’altra, e i teoremi di struttura, che descrivono la struttura (di varietà lineare, di spazio di Banach ecc.) della totalità degli o. lineari continui da una varietà lineare in un’altra.

In particolare, sia Ω la totalità degli o. lineari continui da uno spazio completo di Banach A in sé stesso, il corpo degli scalari essendo il corpo C dei numeri complessi; Ω risulta un’algebra (di Banach), includente C come sottoalgebra. Si dice spettro di un o. ω ∈ Ω l’insieme dei valori complessi z per i quali l’o. ω−z (pure ∈ Ω) non è dotato di inverso entro l’algebra Ω: questo spettro è un insieme S(ω) chiuso e limitato, non vuoto, del piano di Gauss, e il suo studio è di grande interesse per la caratterizzazione dell’o. ω; tra l’altro esso consente di introdurre la nozione di funzione analitica d’o. in modo coerente con le operazioni dell’algebra Ω. Sia f(z) una funzione complessa della variabile complessa z, olomorfa localmente in un campo G del piano di Gauss; dato ω ∈ Ω, con S(ω) ⊂ G si pone

,

dove T è un dominio contenuto in G e contenente S(ω) nell’interno e FT è composto di un numero finito di curve semplici e rettificabili; il valore f(ω) così definito appartiene ancora a Ω e non dipende dalla scelta di T.

Calcolo con o. di Mikusiński

Completamente diverso è il senso del termine operatorio secondo J. Mikusiński e la sua scuola. Sia A l’insieme di tutte le funzioni complesse della variabile reale t, continue a tratti su tutto l’asse reale, ciascuna delle quali nulla in un intorno di −∞: nell’insieme A s’introduce una struttura di anello commutativo, di caratteristica zero, privo di unità, definendo la somma + e il prodotto di convoluzione * nel modo seguente (a,b ∈ A)

Mikusiński chiama o. gli elementi del corpo commutativo generato dall’anello A, ossia le frazioni del tipo a/b, i cui termini a e b sono elementi di A (il secondo diverso dalla funzione identicamente nulla), con l’intesa di considerare uguali le due frazioni a′/b′ e a″/b″ quando è a′*b″=a″*b′, e definendo nel modo consueto le operazioni aritmetiche sulle frazioni. Servendosi di questo corpo di o., Mikusiński dà una fondazione rigorosa ai metodi del calcolo simbolico senza far uso di trasformazioni integrali.

O. logico

In logica matematica è un simbolo che trasforma una forma enunciativa in un enunciato, in un individuo o in un attributo. Gli o. logici del primo tipo si chiamano anche quantificatori, quelli del secondo o. descrittivi e quelli del terzo o. di astrazione.

Forma enunciativa (o funzione proposizionale o enunciato aperto) è un’espressione del linguaggio della logica dei predicati contenente qualche variabile individuale libera; tali sono, per es., le espressioni «x è vivente» (rappresentabile mediante il simbolo Vx) e «x+5=7». Queste espressioni linguistiche non sono enunciati, perché di esse non ha senso dire che sono vere oppure false (➔ logica). I quantificatori sono, dunque, o. che trasformano una forma enunciativa in un enunciato specificando la quantità degli individui (appartenenti a un insieme universale prefissato), ai quali si attribuisce il predicato in questione. Diamo qui un elenco dei quantificatori più usati, con i rispettivi simboli, applicandoli a una generica forma enunciativa, Px:

per ogni x si ha Px:

∀xPx

esiste almeno un x, per cui si ha Px:

∃xPx

esiste esattamente un x, per cui si ha Px:

∃!xPx

esistono esattamente n x, per cui si ha Px:

∃_nxPx.

Il primo quantificatore è detto generalizzatore o quantificatore universale. Applicato al primo esempio (dove si consideri come insieme universale l’insieme di tutti gli uomini), esso trasforma la forma enunciativa Vx nell’enunciato ∀xVx, cioè «per ogni x, (se x è uomo) x è vivente»; tale enunciato risulta evidentemente vero. Se si quantifica universalmente il secondo esempio (dove l’insieme universale è quello dei numeri reali) si ha ∀x(x+5=7), che è un enunciato falso. Il secondo quantificatore si chiama particolarizzatore o, più spesso, quantificatore esistenziale. Applicato alla forma enunciativa x+5=7, la trasforma nell’enunciato, ovviamente vero, ∃x(x+5=7), cioè «esiste un x (nell’insieme dei numeri reali), tale che x+5=7». Si dimostra che tutti i quantificatori possono ridursi ai primi due, anzi a uno qualunque di essi, in quanto valgono le due relazioni

∀x Px ↔ Ó ∃x (Ó Px),

∃x Px ↔ Ó ∀x (Ó Px).

Gli o. descrittivi trasformano una forma enunciativa in un individuo. Tali sono, per es., l’o. iota (simbolo ι) e l’o. mi (simbolo μ, ➔ minimalizzazione), il cui significato appare dalle applicazioni che seguono: ιxVx significa «quell’unico x, tale che x è vivente»; μxVx indica «il più piccolo x, tale che x è vivente»; ιx(x+5=7) sta a indicare evidentemente il numero 2; μx(x²+7x+12=0) designa il numero −4.

L’o. di astrazione non è l’unico, ma il più importante o. che trasforma una forma enunciativa nell’attributo a essa corrispondente. Esso si chiama o. lambda (simbolo λ). Nella logica estensionale ogni attributo si identifica con l’insieme costituito da tutti gli individui cui quell’attributo compete, pertanto λ xVx rappresenta l’attributo «vivente» ovvero «l’insieme di tutti i viventi», mentre la formula λ x(x²+7x+12=0) rappresenta l’insieme {−3, −4}.