omografia

In geometria, corrispondenza biunivoca senza eccezioni tra gli elementi (di solito i punti) che costituiscono due spazi proiettivi P_n e P′_n aventi la stessa dimensione, la quale faccia corrispondere a forme di prima specie di uno di essi forme di prima specie dell’altro. È detta anche proiettività.

Un’o. è rappresentabile mediante una sostituzione lineare omogenea e non degenere sulle coordinate omogenee nei due spazi P_n e P′_n cui l’o. si riferisce, cioè mediante equazioni del tipo:

[1] formula

dove x_j e x′_i sono le coordinate del punto in P_n, e del suo corrispondente in P′_n, ρ è un fattore non nullo e la matrice quadrata dei coefficienti a_ij è non degenere, cioè ha determinante diverso da zero (il che consente la risoluzione del sistema [1] rispetto alle x).

Qualora si utilizzino coordinate non omogenee, la o. si rappresenta mediante n funzioni lineari fratte, aventi lo stesso denominatore. Nel caso particolare di due rette proiettive (spazi P₁ di dimensione uno) l’o. è una corrispondenza biunivoca che conserva i birapporti. In ogni caso una o. è determinata quando si imponga a essa di far corrispondere a n+2 punti assegnati in P_n (tali che n+1 di essi siano sempre indipendenti) n+2 punti assegnati in P′_n.

Costruzione geometrica di un’omografia

fig. 1

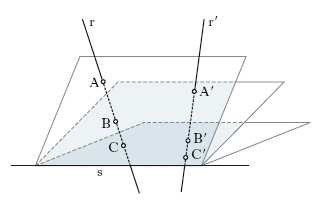
Ogni o. tra due spazi che non abbiano nessun punto in comune è realizzabile mediante un’opportuna operazione di proiezione seguita da una sezione; è il caso, per es., di un’o. tra due rette sghembe (fig. 1): le rette sono r ed r′, i punti corrispondenti A e A′, B e B′ ecc.; la proiezione e la successiva sezione sono attuate tramite il fascio di piani avente per asse una retta s. Se, invece, i due spazi hanno punti in comune, non si può, di solito, realizzare una data o. con una sola proiezione e una sola sezione. Casi particolari di o. sono i movimenti, le simmetrie (rispetto a un punto, o a una retta, o a un piano), le affinità, le omologie ecc.

Studio e classificazione delle omografie

Se gli spazi sono distinti, scegliendo opportunamente il riferimento proiettivo di uno dei due spazi, l’o. si può rappresentare nella forma ρx′_i=x_i (i=0, 1, …, n): gli spazi proiettivi a n dimensioni sono proiettivamente identici e pertanto non si pone nessun problema di classificazione. Se gli spazi sono sovrapposti è possibile una classificazione proiettiva, che si effettua ricercando i punti uniti (cioè i punti che hanno sé stessi per corrispondenti) che caratterizzano l’omografia. Quando si considerino solo o. tra due spazi P_n sovrapposti e si definisca il prodotto di due o. come caso particolare del prodotto di due trasformazioni, l’insieme delle o. è un gruppo continuo a n(n+2) parametri detto gruppo delle proiettività. L’identità del gruppo è l’o. di equazioni ρx′_i=x_i (i=0, 1, …, n), l’inversa della [1] è quella che si ottiene risolvendo il sistema [1] rispetto alle variabili x_i (i=0, 1, …, n).

O. vettoriali

Si chiama o. vettoriale un operatore vettoriale che trasforma vettori in vettori. Precisamente, se v è un vettore, v₁, v₂, v₃ sono le sue componenti rispetto a una terna di riferimento T, e g_rs (r, s=1, 2, 3) sono nove coefficienti di una matrice quadrata M, generalmente variabili al variare di T, si chiama o. vettoriale di coefficienti g_rs l’operatore che trasforma v nel vettore w di componenti w_r=∑³_{1 s}g_rsv_s (r=1, 2, 3). Se si pensano tutti i vettori v e i loro trasformati w applicati in un medesimo punto O, lo spazio dei punti V, estremi dei vettori (O, v), e quello dei punti W, estremi dei vettori (O, w), risultano legati da una di quelle corrispondenze geometriche che hanno il nome di affinità con un punto fisso o anche di epimorfismi di uno spazio vettoriale (ossia di omomorfismi tra spazi coincidenti). Una qualsiasi o. vettoriale ammette sempre almeno una direzione unita (cioè un vettore avente tale direzione viene trasformato dall’o. in un vettore avente la medesima direzione). Particolari o. hanno più d’una direzione unita. Le o. vettoriali sono operatori lineari che si incontrano spesso in questioni di fisica-matematica come, per es., l’o. di tensione nei mezzi deformabili, lo sforzo specifico Φ_u ecc. O. che godono di particolari proprietà assumono denominazioni speciali; si hanno così dilatazioni, dilatazioni pure, rotori, o. assiali, diadi ecc.