poligono

Figura geometrica piana limitata da tre o più segmenti che formino una poligonale chiusa non intrecciata.

Matematica

Geometria

fig. 1A

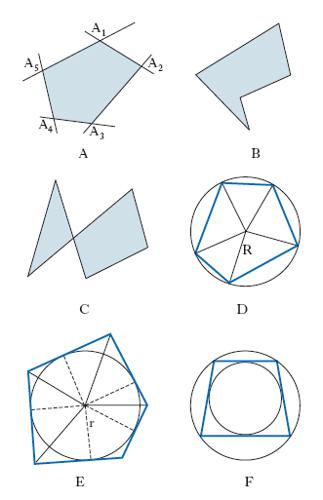
Nella geometria dell’ordinario piano euclideo si chiama p. piano la parte di piano limitata dai segmenti che congiungono, in un ordine prefissato, certi punti distinti A₁, A₂, …, A_n del piano, e l’ultimo col primo, tali che tre consecutivi non siano allineati e che i segmenti considerati non abbiano punti comuni, all’infuori dei punti fissati. I punti A₁, A₂, …, A_n si dicono vertici del p., i segmenti suddetti si dicono lati del p. e la somma dei lati si dice perimetro. Il p. così definito si dice più propriamente p. ordinario o non intrecciato. Se inoltre i prolungamenti dei lati non attraversano il p., questo si dice convesso (fig. 1A); se i prolungamenti dei lati attraversano il p., si dice concavo (fig. 1B). In un p. concavo può accadere che lati non consecutivi abbiano un punto comune: si ha allora un p. intrecciato (fig. 1C). In un p. convesso gli angoli formati da 2 lati consecutivi si dicono angoli interni (o brevemente angoli) del p. e gli angoli a essi adiacenti angoli esterni; la somma degli angoli esterni è sempre uguale a 4 angoli retti, mentre la somma degli angoli interni è n –2 angoli piatti. Un p. con 3, 4, 5, 6, …, 10, … lati si dice rispettivamente triangolo, quadrangolo, pentagono, esagono, …, decagono … ecc.

fig. 2

tab.

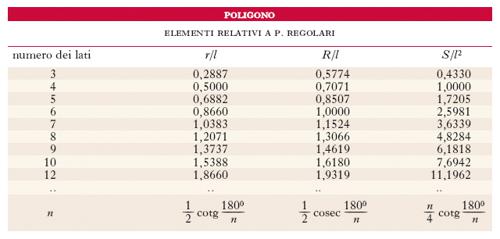
Un p. è inscrivibile se esiste una circonferenza che passa per i suoi vertici (fig. 1D) e, in tal caso, si può decomporre in triangoli isosceli il cui lato R si chiama raggio del poligono. Un p. si chiama circoscrivibile se esiste una circonferenza tangente a tutti i suoi lati (fig. 1E). Si chiama apotema di un p. circoscrivibile la distanza r di ciascun lato del p. dal centro della circonferenza tangente ai lati. Alcuni p. possono essere inscrivibili e circoscrivibili (fig. 1F). P. piano completo In geometria proiettiva è la configurazione formata da n punti a 3 a 3 non allineati e dalle n(n–1)/2 rette che li congiungono a 2 a 2 in tutti i modi possibili. La fig. 2 illustra il caso n = 5. P. nel piano proiettivo Nel piano proiettivo la nozione di p. si può presentare sotto vari aspetti: uno di essi corrisponde ai p. piani completi; un altro si ottiene invece considerando n punti A₁, A₂, …, A_n ordinati circolarmente (vertici del p.) e assumendo come lati del p. uno qualsiasi dei due segmenti proiettivi di estremi A₁A₂, uno qualsiasi di quelli di estremi A₂A₃, e così via fino ad A_nA₁. Si nota subito che i punti A₁, A₂, …, A_n individuano non un solo p., ma 2ⁿ poligoni. P. regolare È un p. al tempo stesso equilatero ed equiangolo: cioè tutti i lati e tutti gli angoli sono eguali tra loro. Se i vertici sono in numero di n, gli angoli interni valgono 180°–(360°/n) e gli angoli esterni 360°/n. Un p. regolare è contemporaneamente inscrivibile e circoscrivibile: le due circonferenze che si ottengono sono concentriche, il loro centro si chiama centro del p. e, come si è detto, i loro raggi rispettivamente raggio e apotema del p. regolare. Nella tab. sono riportati il rapporto al lato l dell’apotema r e del raggio R e il rapporto al quadrato del lato dell’area S per alcuni p. regolari e per il caso generale di un p. regolare di n lati; i fattori della seconda colonna sono talvolta chiamati numeri fissi.

fig. 3

fig. 4A

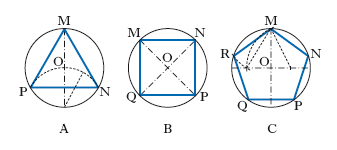
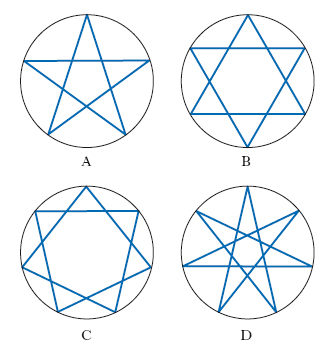
Risalgono agli antichi Greci le costruzioni, mediante riga e compasso, dei p. regolari di n lati per n = 3, 4, 5 (fig. 3) e per i valori ottenuti da questi mediante ripetute moltiplicazioni per 2. Il problema di quali altri valori di n corrispondano a p. regolari costruibili con riga e compasso fu completamente risolto da K.F. Gauss che ricondusse il problema alla soluzione, nel campo complesso, dell’equazione xⁿ = 1 (detta della ciclotomia ossia della divisione del cerchio in parti uguali). Il risultato di Gauss è che il p. regolare di n lati è costruibile elementarmente se e solamente se il numero n, previa un’eventuale divisione per una potenza di 2, è un prodotto di numeri primi del tipo 2²ⁿ+1 (numeri primi di Fermat) tutti diversi tra loro. P. regolare stellato È un particolare p. intrecciato che si ottiene dividendo una circonferenza in n parti uguali e, fissato su essa un verso di percorrenza, congiungendo ciascun punto di divisione con quello che, nel verso prescelto, si ottiene saltando un punto (oppure 2, o più). Il più semplice p. regolare stellato si ha per n = 5 (fig. 4A): esso era stato assunto come emblema dalla scuola pitagorica e fu poi tramandato con il nome di pentalpha o di pentagramma mysticum; per n = 6 si ha un p. stellato costituito da due triangoli equilateri (fig. 4B) mentre per n = 7 si hanno ettagoni stellati di due differenti tipi (fig. 4C, D). P. sferico P. tracciato sopra una superficie sferica e che ha come lati archi di cerchio massimo. L’area di un p. sferico è data dal prodotto πRε/180°, essendo R il raggio della sfera e ε l’eccesso sferico del poligono.

Statica grafica

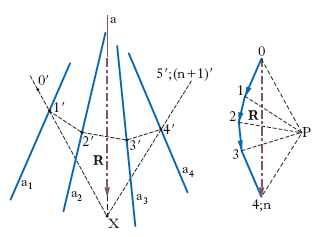
In statica grafica, p. funicolare è una poligonale piana, in generale aperta, avente i vertici sulle rette di applicazione dei vettori di un sistema piano, la cui considerazione è di fondamentale importanza nei problemi di riduzione di siffatti sistemi. Sia assegnato un sistema Σ di n vettori applicati v_i, appartenenti a un medesimo piano π, che penseremo numerati a piacere, e siano a_i le rispettive rette di applicazione. A partire da un arbitrario punto 0 del piano π (fig. 5), costruiamo la poligonale dei vettori 0 1 2… n che con i suoi estremi caratterizza il risultante R (≡ 0 n) di Σ. Scelto a piacere in π un punto P, con l’unica condizione che esso non giaccia su alcuna delle rette cui appartengono i lati della poligonale, proiettiamo da esso i vertici di questa: le semirette P0, P1, …, Pn si chiamano primo, secondo, …, ultimo raggio proiettante.

Nel piano π conduciamo una retta parallela al primo raggio proiettante e indichiamo con 0′ un suo punto generico e con 1′ la sua intersezione con a₁, retta d’applicazione del vettore v₁; dal punto 1′ conduciamo la parallela al secondo raggio proiettante e indichiamo con 2′ l’intersezione con la retta di applicazione a₂ di v₂, e così di seguito. La poligonale 0′ 1′ 2′ … (n+1)′ che in tal modo si costituisce ha appunto il nome di p. funicolare relativo all’assegnato sistema di vettori. I punti 0′, 1′, 2′, …, (n+1)′ sono i vertici del p. funicolare; le rette 0′1′, 1′2′, …, n′ (n′+1) ′ i suoi lati. Si suole anche dire che il p. ‘connette’ il sistema. La qualifica di funicolare è dovuta al fatto che la configurazione di equilibrio di una fune soggetta a forze concentrate complanari è un p. funicolare connettente tali forze. Il punto P si dice polo del poligono.

fig. 5

fig. 6

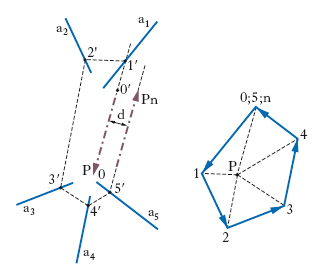
Il metodo del p. funicolare consente di istituire sistematici procedimenti di riduzione di un sistema piano di vettori applicati ai due vettori 0P e Pn applicati rispettivamente al primo e all’ultimo lato di un p. funicolare di polo P che connetta il sistema. In caso di sistemi a risultante non nullo, il sistema è riducibile al risultante R applicato all’asse centrale a (parallela a R condotta per il punto X d’incontro del 1° e ultimo lato del p. funicolare: fig. 5). Nei sistemi a risultante nullo la poligonale dei vettori risulta chiusa: il punto 0 coincide con il punto n (fig. 6), il 1° e l’ultimo lato del p. funicolare risultano paralleli, il sistema è riducibile a una coppia il cui vettore ha per modulo la comune lunghezza di 0P e Pn, e il cui braccio è la distanza d tra il primo e l’ultimo lato del p. funicolare, ai quali sono rispettivamente applicati 0P e Pn. Se, in particolare, il primo e l’ultimo lato vengono a essere sovrapposti, la coppia riesce di braccio nullo: si dice allora che il sistema è riducibile a zero o equilibrato.

Anatomia

P. arterioso di Willis Circolo arterioso impari e mediano, situato sulla faccia inferiore dell’encefalo e costituito, anteriormente dalle due arterie cerebrali anteriori (rami terminali della carotide interna) unite dall’arteria comunicante anteriore, posteriormente dalle due arterie cerebrali posteriori (diramazioni del tronco basilare formato dalla fusione delle due arterie vertebrali) e lateralmente dalle due arterie comunicanti posteriori o laterali (rami della carotide interna).

Scienza militare

P. di tiro Tratto di terreno ben delimitato e predisposto per l’esecuzione di tiri a proietto con armi da fuoco. Per estensione, il termine è usato anche per indicare le basi di lancio di missili: p. astronautico o spaziale, lo stesso che base spaziale o cosmodromo (➔ missile). I p. di tiro possono essere chiusi o aperti.