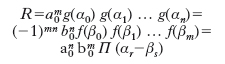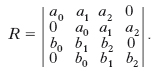risultante
Fisica
In analisi vettoriale, di un sistema di vettori, liberi o applicati, si dice r. o somma vettoriale il vettore che si ottiene come risultato dell’operazione di composizione. In particolare, il r. di due vettori è la diagonale del parallelogramma costruito sui due vettori (regola del parallelogramma); il r. di tre vettori non complanari è la diagonale del parallelepipedo costruito sui tre vettori (regola del parallelepipedo). Il r. è un vettore libero, del quale cioè non è specificato il punto di applicazione. Quando di un sistema di vettori applicati si effettua la riduzione al più semplice sistema equivalente, questo risulta costituito, in generale, dal r. applicato all’asse centrale del sistema stesso più una opportuna coppia, potendo in casi particolari mancare uno dei due elementi. Il r. di un sistema di vettori ha modulo generalmente minore della somma dei moduli dei singoli vettori, a questa risultando uguale soltanto quando i vettori sono tutti paralleli e concordi. Se dei singoli vettori del sistema sono assegnate le componenti rispetto a una certa terna cartesiana di riferimento, sussiste la proprietà che le componenti del r. secondo i singoli assi coincidono con la somma algebrica delle componenti omologhe dei singoli vettori.
È detta r. aerodinamica la r. di tutte le forze agenti sulla superficie di un corpo in moto relativo rispetto a un fluido. Tale r. si scompone generalmente in due forze, la resistenza, che è diretta come la corrente, e la portanza, che è normale alla corrente.
Matematica
La r. di due polinomi f(x), g(x) di grado rispettivamente n ed m è un certo polinomio R nei coefficienti ai di f(x) e bi di g(x) il cui annullarsi è condizione necessaria e sufficiente perché le due equazioni f(x)=0, g(x)=0 abbiano almeno una radice comune. Se
[1] formula
e si indicano con α0, α1, …, αn gli zeri di f(x) e con β0, β1, …, βm quelli di g(x), espressioni analitiche del r. sono:
(nell’ultima di esse il prodotto va eseguito facendo variare gli indici r, s da 0 a n e, rispettivamente, da 0 a m). Un’espressione esplicita del r. per mezzo dei coefficienti a0, …, an, b0, …, bm, ottenuta da J.J. Sylvester con il suo ‘metodo dialitico’, è data dal determinante di ordine m+n:
Per es., se f(x), g(x) sono due polinomi di 2° grado, f(x)=a0x2+a1x+a2, g(x)=b0x2+b1x+b2, il loro r. è il seguente determinante del 4° ordine:
In generale, il r. dei polinomi [1] è un polinomio nelle m+n+2 variabili a0, …, an, b0, …, bm: esso ha grado m+n ed è irriducibile, ossia non decomponibile nel prodotto di polinomi di grado inferiore. Affinché le equazioni f(x)=0, g(x)=0 abbiano k radici comuni occorre e basta che la matrice [2] abbia caratteristica m+n−k, o anche che risulti R=R1=…=Rk−1=0 e Rk ≠ 0 avendo indicato con R1 il determinante della matrice di ordine m+n−2i che si ottiene dalla [2] sopprimendovi le ultime i righe contenenti i coefficienti a, le ultime i righe contenenti i coefficienti b e le ultime 2i colonne.
Supposto n≥m il r. di f(x), g(x) può anche scriversi, seguendo É. Bézout (➔), sotto forma di un determinante di ordine n (detto bézoutiante). Ha particolare interesse il r. di un polinomio f(x) e della sua derivata f′(x) (➔ discriminante).
La teoria del r. si può estendere al caso dei polinomi in due o più variabili. Precisamente, considerati m+1 polinomi in m variabili: ϕi(x1, x2, …, xm) con i=1, 2 …, m+1, di gradi n1, n2, …, nm+1 e con coefficienti del tutto indeterminati, esiste una funzione razionale intera R di questi coefficienti (che si chiama r. dei polinomi ϕi) che si annulla quando e solo quando le equazioni ϕi=0 hanno una soluzione comune. Segue da ciò il celebre teorema di Bézout sul numero delle soluzioni di un sistema di equazioni algebriche.