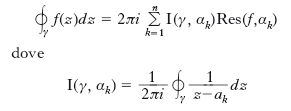residuo

Economia

Nella contabilità di Stato, r. di bilancio attivi o passivi, rispettivamente le entrate accertate ma non incassate e le spese impegnate ma non pagate entro l’anno finanziario relativo.

Nel sistema dei bilanci di competenza, i r. degli esercizi anteriori sono tenuti distinti dalle entrate e spese il cui diritto o il cui obbligo maturano in un dato anno; se si segue invece il sistema del bilancio di cassa, non si fa distinzione tra le varie entrate o spese che dovrebbero avere materiale esecuzione nell’anno a qualsiasi momento risalga la loro ragione giuridica. Le somme previste in bilancio, ma non impegnate, non costituiscono r., ma economie di bilancio; però nella nostra azienda statale si considerano r. passivi (r. di stanziamento) anche alcune somme, che dovrebbero figurare tra le economie (in quanto non ancora legalmente impegnate), ma che, essendo relative a spese dovute annualmente per legge o riguardando opere, lavori, forniture in corso, in attesa del perfezionamento dell’atto d’impegno si portano fra i r. per avere i fondi necessari a eseguire i pagamenti relativi a liquidazione avvenuta.

Matematica

Il r. integrale (o brevemente r.) di una funzione analitica f(z) in un suo punto regolare o singolare isolato z₀, si indica abitualmente con Res(f, z₀) ed è dato da

dove l’integrale è esteso a un circuito regolare γ percorso in senso antiorario che racchiuda z₀ al suo interno e che sia convenientemente piccolo, in modo da non contenere nessun punto singolare di f(z) salvo, tutt’al più, z₀ stesso. Il r. di f(z) in z₀ è anche uguale al coefficiente di 1/(z−z₀) nello sviluppo in serie di Laurent di f(z) con punto iniziale z₀, ed è nullo se z₀ è un punto regolare. L’introduzione dei r. integrali, di grande importanza nella teoria delle funzioni di variabile complessa, è dovuta ad A. Cauchy (1820). Teorema dei r. Sia Ω un aperto semplicemente connesso del piano complesso e sia f una funzione definita in Ω e olomorfa in Ω/{α₁, …, α_n}, essendo {α₁, …, α_n} i punti di singolarità di f in Ω; sia inoltre γ una curva chiusa contenuta in Ω/{α₁, …, α_n}, allora si ha

è l’indice di avvolgimento, un intero che indica il numero di volte che la curva γ si avvolge intorno alla singolarità α_k e che è positivo (negativo) se la curva è percorsa in senso antiorario (orario) e nullo se la curva non racchiude α_k. Il teorema dei r. è molto utile per calcolare integrali di linea di funzioni meromorfe su curve chiuse o anche integrali reali. R. quadratico In teoria dei numeri, un intero a si chiama r. quadratico di un intero k primo con a (o anche r. quadratico modulo k) se aggiungendo o sottraendo ad a un conveniente multiplo di k si può ottenere un quadrato.