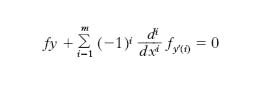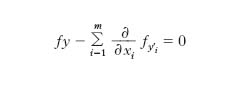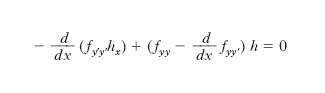variazione
Matematica
Calcolo delle variazioni
Ramo della matematica che studia i metodi per ottenere i massimi e i minimi di un insieme di elementi (in generale funzioni) considerati come punti di un opportuno spazio metrico. Il primo problema che portò a questi studi fu posto da I. Newton (1686): quale deve essere la forma di un solido di rotazione con volume e lunghezza del profilo assegnati affinché la resistenza incontrata nel movimento secondo la direzione del suo asse sia minima? Sotto opportune ipotesi il problema si traduce in quello di determinare una funzione y(x) (profilo del solido di rotazione) con x variabile in un intervallo [a,b] in modo tale che risulti minimo l’integrale
dove y′ è la derivata di y. Un secondo problema, detto della curva brachistocrona, fu risolto da Giovanni Bernoulli nel 1696 trovando la cicloide, curva grafica di una funzione che rendeva minimo l’integrale
Un altro problema risolto da Giovanni Bernoulli (1697) fu quello della geodetica (➔), ma fu principalmente Giacomo Bernoulli che portò un contributo notevole a questi studi con la risoluzione (1687) del problema dell’isoperimetro (➔).
Il più semplice problema di calcolo delle v. consiste nel trovare una funzione y(x) che rende minimo un integrale della forma
con f continua in un ‘cilindro’ dello spazio R3 che ha per sezione sul piano z=0 un dominio semplicemente connesso. La prima soluzione, ottenuta da Eulero (1744) e, in maniera più rigorosa, 15 anni più tardi da G. Lagrange, si basa sul concetto di v. prima di un funzionale, che è simile a quella di differenziale per una funzione. Supposto che la funzione y(x) definita tra x0 e x1 sia la soluzione cercata, si considera una funzione g(x) definita sull’intervallo x0, x1, nulla agli estremi, con derivata seconda continua; si considera poi la funzione ȳ(x)=y(x)+εη(x), dove ε è un parametro. La quantità εη(x) si dice v. prima della funzione y(x); se ε è sufficientemente piccolo le funzioni ȳ(x) sono in un intorno abbastanza piccolo della funzione estremale y(x). L’integrale I(ȳ)=I(y+εη) si può pertanto considerare come una funzione della variabile ε, e deve quindi avere un minimo relativo per ε=0; pertanto dovrà essere nulla la v. prima del funzionale I,
Ciò conduce, dopo ulteriori calcoli in ipotesi di regolarità per la f, all’equazione differenziale di Eulero (o di Eulero-Lagrange) del secondo ordine
dove il primo membro è la derivata v. di f rispetto a y. Una soluzione della [3] viene detta curva stazionaria o di stazionarietà. Tra le varie generalizzazioni della [1], una consiste nel considerare a e/o b mobili con leggi assegnate; per es., nel caso che a appartenga alla curva di equazione g(x, y)=0, la funzione estremale è soggetta alla condizione di trasversalità (f−y′fy′)gy−fy′gx=0. Se, invece, la funzione integranda della [1] contiene n funzioni incognite y1, y2, ..., yn, con le rispettive derivate prime, il sistema di Eulero è formato da n equazioni, del tipo [3], per le n funzioni incognite. Se la funzione integranda dipende anche dalle derivate di y fino all’ordine m (m>1), l’equazione di Eulero è
con fy(i)= ∂f/∂y(i), e y(i)=diy/dxi. Quando la funzione incognita y dipende da n variabili x1, x2, ..., xn, la [3] diviene
con y′i=∂y/∂xi.
Condizioni necessarie affinché y(x) fornisca un minimo per I[y] è che sia verificata la diseguaglianza fy′y′(x,y,y′)≥0 (A.-M. Legendre, 1786), oppure, condizione di Jacobi (1837), che la soluzione dell’equazione nell’incognita h(x),
non abbia zeri nell’intervallo [a,b]. La condizione di Weierstrass (1879) è che risulti ℰ≥0 essendo ℰ(x, y, y′, p)=f(x, y, y′)− f(x, y, p)−(y′−p)fy′ (x, y, p). Una condizione sufficiente perché y(x) sia di minimo per I fu presentata da K. Weierstrass nel 1870; da allora gli studi presero nuovo impulso e furono diretti più verso l’esistenza di eventuali soluzioni che non verso il loro effettivo reperimento.
Altri metodi, cosiddetti diretti, per la determinazione delle soluzioni della [1] si basano sulla trasformazione del problema di massimo (o di minimo) di un funzionale in uno equivalente di estremale di una funzione di più variabili. Nel metodo di Eulero (1768) si sostituisce, nella f di [1], la curva y(x) con una poligonale basata su una partizione dell’intervallo [a,b] e, su ciascun subintervallo, la derivata y′(x) con il rapporto incrementale, riducendo I[y] a funzione delle ordinate dei vertici della poligonale. Tale metodo che, fino all’avvento degli elaboratori elettronici, fu poco diffuso per la grande quantità dei calcoli necessari ha conosciuto successivamente notevoli estensioni. Il metodo di Ritz, in cui la soluzione y(x) si assume combinazione lineare di un numero finito di opportune funzioni assegnate, consiste nella riduzione di I[y] a funzione dei coefficienti della combinazione e nella successiva determinazione di questi. Se il metodo si applica direttamente al sistema di equazioni differenziali viene anche detto metodo di Galerkin.
In relazione ad alcune questioni di fisica matematica, E. Volterra (1884) diede un impulso fondamentale all’analisi funzionale con lo studio delle equazioni differenziali, integrali e integro-differenziali, le cui incognite sono funzioni. Importanti contributi vennero successivamente dai lavori di C. Arzelà (1897), D. Hilbert (1900), B. Levi (1906), G. Fubini (1906), H.-L. Lebesgue (1907) e soprattutto di L. Tonelli (1911). Sviluppi notevoli hanno avuto gli studi sulla superficie di area minima, come soluzioni del problema di Plateau e del problema connesso al principio di Dirichlet (rendere minimo l’integrale del modulo di un gradiente).
Parallelamente, si è sviluppata un’altra forma del calcolo delle v., il cosiddetto calcolo delle v. in grande; a essa ha dato impulso, tra gli altri, M. Morse, che ha anche utilizzato, a tale scopo, metodi propri della teoria dei punti critici e dell’omologia. In particolare, il calcolo delle v. in grande si occupa di problemi anche topologici relativi all’esistenza e alla stima del numero delle funzioni estremali su una varietà e allo studio delle corrispondenti proprietà qualitative mediante l’analisi di punti critici.
In una nuova classe di problemi, detti problemi con discontinuità libera, il funzionale da minimizzare dipende da una funzione u che risulta discontinua su una superficie S a priori incognita. In generale questo funzionale contiene un integrale di volume, sul complementare di S, dipendente dalla funzione u e dalle sue derivate, e un termine dipendente dalla superficie S di discontinuità. Questi problemi uniscono dunque le caratteristiche dei problemi di minimo per funzioni integrali con quelle dei problemi di tipo geometrico. Il prototipo dei problemi con discontinuità libera fu proposto nel 1985 da D. Mumford e J. Shah e, nel caso n=2, esso è collegato a problemi di segmentazione d’immagine nella teoria della visione artificiale. Data una regione limitata Ω dello spazio euclideo n-dimensionale e una funzione limitata g definita su Ω, il problema consiste nel trovare il minimo del funzionale
dove ΩS indica l’insieme dei punti di Ω che non stanno in S e Hn−1(S) indica la misura (n−1)-dimensionale di S. La principale novità di questo problema consiste nel fatto che vi sono due variabili rispetto a cui va cercato il minimo: una è l’insieme S, che varia tra i sottoinsiemi di Ω di misura (n−1)-dimensionale finita, e l’altra è la funzione u, che varia tra le funzioni continue e dotate di derivate parziali continue su ΩS. Questo problema è stato risolto dimostrando con i metodi diretti l’esistenza di un’opportuna soluzione generalizzata appartenente a un nuovo spazio funzionale, introdotto da L. Ambrosio ed E. De Giorgi nel 1988, detto spazio delle funzioni a v. limitata di tipo speciale, e dimostrando poi che la soluzione generalizzata così trovata fornisce una soluzione del problema proposto. Successivamente (1995) è stato dimostrato che per un punto di minimo (u, S) l’insieme S è una varietà regolare di dimensione n−1, a meno di un insieme singolare avente misura (n−1)-dimensionale nulla. La regolarità della funzione u segue a questo punto dai risultati classici di regolarità per i minimi dell’integrale di Dirichlet. Rimangono aperti problemi interessanti a proposito della struttura dell’insieme singolare della varietà S, in particolare quello di stabilire se per n=2 questo insieme singolare sia costituito da un numero finito di punti. Funzionali del tipo considerato da Mumford e Shah, oltre che in teoria della visione, si incontrano anche in varie questioni di fisica matematica.
Funzioni a v. limitata
È tale una funzione reale f della variabile reale x, definita sull’intervallo chiuso [a, b] se, qualsiasi sia la suddivisione di [a, b] in sottointervalli [xi−1, xi] tali che
a=x0<x1<x2< ... <xn=b, la somma
∑ni=1 ∣f(xi) − f(xi−1)∣ sia limitata da uno stesso
numero M indipendente dalla suddivisione; l’estremo superiore di tale somma si dice v. totale di f su [a, b]. Ogni funzione a v. limitata risulta differenza di due funzioni monotone; viceversa, ogni differenza o somma tra funzioni monotone sull’intervallo chiuso [a, b] risulta a v. limitata.
Musica
Tecnica compositiva che consiste nella modificazione di un pensiero musicale in sé compiuto ottenuta intervenendo sulla melodia, sul ritmo, sull’armonia, sulla strumentazione (ove vi siano più strumenti), sulle combinazioni contrappuntistiche di esso, operando in modo tale da consentire la riconoscibilità del tema di partenza. Come suoi procedimenti tipici possono essere indicati l’ornamentazione della figura musicale di base, la sua collocazione in un contesto contrappuntistico, la modificazione del suo contesto armonico, il cambiamento della sua struttura ritmica, agogica, dinamica, timbrica ecc. In pratica ciascuno di questi procedimenti si combina con altri, non raramente con tutti gli altri, dando luogo a una ricchissima molteplicità di combinazioni.
Come forma musicale, la v. iniziò il suo sviluppo nel primo Cinquecento in Spagna e in Inghilterra, nei brani per liuto e per strumenti a tastiera; in quest’ultimo ambito si segnalarono presto sia i compositori tedeschi e fiamminghi (in particolare J.P. Sweelinck), sia quelli italiani (che ebbero in G. Frescobaldi il rappresentante più significativo). Nella Germania protestante andò sviluppandosi la v. su melodie di corale (destinata a culminare nell’opera di J.S. Bach). Con il classicismo viennese, e in particolare con L. van Beethoven, la v. fu assunta a tecnica compositiva privilegiata, sia come strumento per rivivificare dall’interno le grandi forme (in particolare la forma-sonata), sia come pezzo a sé: il cosiddetto ‘tema con v.’, in cui a un tema iniziale, solitamente breve e di semplice stesura, seguono un certo numero di ripetizioni variate: Variazioni su un tema di Haydn di J. Brahms (op. 56 a); 33 Variazioni su un Valzer di Diabelli, di Beethoven (op. 120). La tecnica della v. passò poi, attraverso i romantici, alla scuola di Vienna e da essa alla musica contemporanea, che ne ha radicalmente ripensato i presupposti, facendone la base del suo pensiero compositivo.


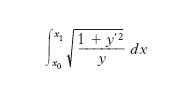
![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/bd/FORMULE_variazione_01.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/c/c5/FORMULE_variazione_02.jpg)
![[3]](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/30/FORMULE_variazione_03.jpg)