inviluppo

In genere, qualsiasi cosa che avvolge strettamente.

Matematica

Inviluppo di una famiglia di curve piane È una curva L tale che per ogni suo punto P passi una e una sola curva della famiglia data avente ivi la stessa tangente della L. Se f(x, y, t)=0 è l’equazione delle curve C_t della famiglia, sotto opportune condizioni di continuità, derivabilità ecc., l’i. esiste, e la sua equazione si ottiene eliminando il parametro t dal sistema

[1]

fig. 1

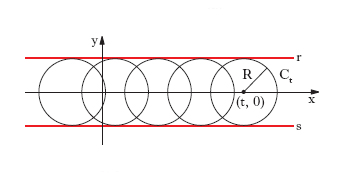
dove f_t è la derivata di f(x, y, t) rispetto a t. Per es., la famiglia costituita dai cerchi C_t aventi centro variabile sull’asse x (nel punto di questa retta avente ascissa t) e raggio R (fig. 1), ha equazione

x² + y² − 2tx + t² − R² = 0

fig. 2

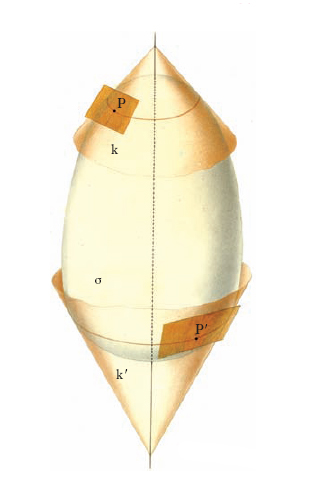
e ha come i. la curva costituita dalla coppia di rette r, s, di equazioni y=R, y=−R. In generale, però, la curva ottenuta eliminando t dal sistema [1] sarà costituita, oltre che dall’i. vero e proprio, anche dalle curve luogo delle singolarità delle curve C_t della famiglia considerata. I. di una famiglia di superfici È una superficie σ tale che per ogni suo punto P passi una e una sola superficie della famiglia avente ivi lo stesso piano tangente di σ. Per es., una superficie di rotazione σ (fig. 2) è l’i. della famiglia di coni che hanno vertici nei vari punti dell’asse di σ e sono circoscritti a tale superficie; in figura sono rappresentati due coni k, k′ e i piani tangenti a σ nei due punti P, P′. Se f(x, y, z, t)=0 è l’equazione delle superfici della famiglia (al variare del parametro t), l’equazione della superficie i. si ottiene eliminando il parametro t dal sistema

[2]

fig. 3A

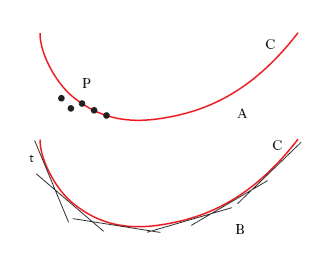
Curva i. È il concetto duale di curva luogo; una curva C infatti può essere concepita o come l’insieme (il luogo) dei suoi punti P (fig. 3A) o come l’i. delle tangenti t a essa (fig. 3B). Se la curva è algebrica, l’i. delle sue tangenti è un ente algebrico: ciò vuol dire che esiste un’equazione algebrica, in coordinate di retta, soddisfatta da tutte e sole le rette tangenti alla curva. La nozione si estende alle superfici: l’i. aderente a una superficie luogo è costituito dall’insieme dei piani tangenti a essa ecc.

Tecnica

I. di modulazione In elettronica, la linea che si ottiene congiungendo i successivi picchi di un’oscillazione modulata in ampiezza; se la modulazione è di buona qualità, l’i. di modulazione riproduce fedelmente la forma d’onda del segnale modulante.