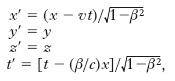relatività

relatività In fisica, in riferimento a un ente fisico o a un fenomeno, dipendenza delle proprietà o grandezze dal sistema di riferimento adottato. Tali grandezze o proprietà assumono significati e valori univoci solo se si è convenzionalmente fissato un criterio di riferimento (per es., un sistema di coordinate), cosicché tali significati e tali valori non possono essere considerati assoluti e inerenti all’ente fisico stesso, ma vanno al contrario concepiti come relativi, in quanto variano se il sistema di riferimento viene, per una qualsiasi ragione, cambiato.

Teorie della relatività

fig. 1

fig. 2

fig. 3

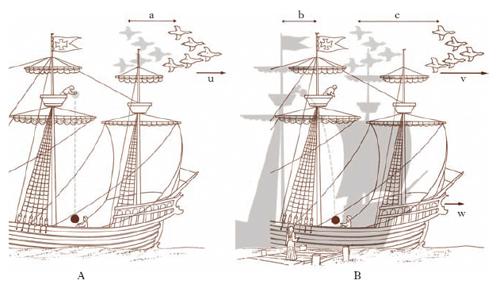
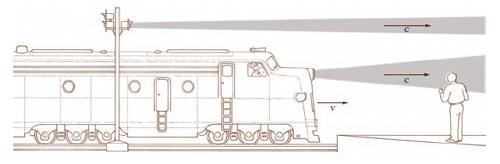
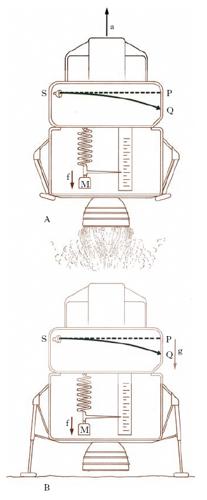
Il principio di r. galileiano (fig. 1) afferma che nessuna esperienza eseguita nell’interno di un sistema può rivelarne un moto traslatorio rettilineo uniforme, rispetto a un riferimento fisso o, più genericamente, inerziale; in altri termini, qualsiasi esperienza o osservazione eseguita nell’interno di un corpo è atta a rivelarne un moto relativo soltanto a patto che questo non sia un moto traslatorio rettilineo uniforme. Nella formulazione galileiana del principio l’impossibilità di cui si è detto è limitata alle esperienze meccaniche. A. Einstein affermò (1905) che tale impossibilità sussiste per esperienze di qualsiasi natura: è questo il principio di r. einsteiniano (fig. 2), che è tra i postulati fondamentali delle varie teorie della r. e in particolare della teoria della r. ristretta (o speciale) dovuta (1905-07) allo stesso Einstein. A questa teoria seguiva, in una seconda fase (1912-16), per una più profonda indagine delle proprietà del continuo spazio-temporale che costituisce la sede di qualsiasi evento, la r. generale. Nella r. generale (fig. 3) quelle fondamentali proprietà della materia che sono la gravitazione e l’inerzia venivano a essere riportate a uno stesso principio, potendosi considerare ambedue come dovute alle proprietà geometriche dello spazio-tempo o, fisicamente, alla distribuzione, variabile nel tempo, della materia e dell’energia. In una terza fase (1918-50) si svilupparono le teorie unitarie (da H. Weyl ad Einstein), volte a ridurre a unità i fenomeni gravitazionali ed elettromagnetici, attraverso la costruzione di un unico modello geometrico per i due campi, appunto gravitazionale ed elettromagnetico.

R. ristretta

Un evento è il verificarsi di un fatto che ha sede nello spazio e nel tempo; come tale esso si può pensare matematicamente individuabile mediante 4 coordinate: 3 spaziali, che determinano il luogo in cui l’evento si è verificato, una temporale, che fissa l’istante in cui esso si è verificato. Naturalmente, non avrebbe senso parlare di coordinate se non con riferimento a un osservatore O che le misuri; ed egli le misurerà, quelle spaziali, per es. sugli assi di una prefissata terna cartesiana, quella temporale su un suo orologio (cioè, in termini matematici, su un prefissato asse dei tempi). Siano x, y, z, t i risultati delle misurazioni effettuate da O. Un secondo osservatore O′, in moto rispetto a O, faccia per lo stesso evento analoghe determinazioni servendosi di un’altra analoga quaterna di assi e siano x′, y′, z′, t′, i risultati delle misurazioni effettuate da O′ in relazione all’evento considerato. La meccanica classica postula due fatti: a) posto che i due orologi siano stati preventivamente sincronizzati, l’evento si verificherà per i due osservatori al medesimo istante, si avrà cioè t=t′, ciò che è quanto postulare l’esistenza di un tempo assoluto; b) la distanza fra due punti prefissati è la stessa tanto che sia misurata da O quanto che sia misurata da O′. Dai due postulati a) e b) discendono nella loro forma classica il principio dei moti relativi e il teorema di Coriolis, che legano fra loro, in un moto relativo, le velocità il primo, le accelerazioni il secondo. Ammessa, come si ammetteva, l’esistenza di un etere cosmico in quiete assoluta nell’Universo, una conseguenza del principio dei moti relativi è che la velocità della luce valutata da un osservatore terrestre dovrebbe dipendere dalla direzione da cui proviene il segnale. Ma le esperienze, in primo luogo quella celebre di A.A. Michelson (1881), smentiscono tale previsione, ponendo in discussione, in ultima analisi, da un lato la validità dei postulati a) e b), dall’altro l’ipotesi dell’etere stagnante e anzi l’esistenza stessa dell’etere. È di qui che trae le sue origini la teoria della r. ristretta. A fondamento di essa sono il principio di r. einsteiniano, secondo il quale nessuna esperienza, di qualsiasi natura, eseguita nell’interno di un sistema, può rivelare il moto di traslazione rettilinea uniforme del sistema rispetto a un riferimento inerziale; e il principio della costanza della velocità della luce, secondo il quale la velocità della luce nel vuoto è una costante indipendente dal moto della sorgente e dell’osservatore.

fig. 4

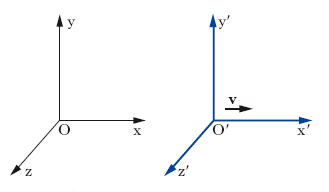
L’adozione dei due postulati della r. ristretta comporta l’abbandono dei postulati a) e b), dai quali in sostanza discendeva il carattere di grandezze assolute attribuito al tempo e alle lunghezze. Ci si può rendere conto delle alterazioni che queste subiscono per effetto dell’abbandono dell’impostazione classica nel modo seguente. Due triedri (fig. 4) Oxyz, O′x′y′z′ siano in moto traslatorio rettilineo uniforme l’uno rispetto all’altro; per semplicità si può pensare, per es., che all’istante iniziale i 2 triedri, ortogonali, risultino sovrapposti, che il primo triedro sia fermo, mentre O′ scorre lungo l’asse x con velocità (costante) v: allora l’asse x′ resta costantemente sovrapposto a x, mentre gli assi y′ e z′, conservando l’orientamento iniziale, risultano a ogni istante orientati rispettivamente come y e z. Tanto in O quanto in O′ vi sia un osservatore e ambedue gli osservatori abbiano la possibilità di misurare le coordinate spazio-temporali di un evento. Un evento qualsiasi sarà individuato da O o da O′ quando essi ne abbiano misurate le coordinate x, y, z, t e, rispettivamente, x′, y′, z′, t′, dette coordinate galileiane dell’evento, relative ai due riferimenti: si tratta di riconoscere quali relazioni passino fra tali coordinate. Si supponga per semplicità che l’evento consista nell’emissione di un segnale luminoso dal punto in cui si trovano O e O′ all’istante iniziale (in cui essi sono sovrapposti). Ammesso che la sorgente sia puntiforme e il mezzo sia isotropo, il segnale si propagherà per onde sferiche concentriche di raggio crescente; se si ammette il principio della costanza della velocità della luce e si indica con c tale velocità, il generico fronte d’onda avrà per l’osservatore O equazione x²+y²+z²=c²t², e per l’osservatore O′ equazione x′²+y′²+z′² =c²t′². Esprimendo opportunamente x′, y′, z′ e t′ in funzione di x, y, z, t e v e imponendo che le due equazioni si identifichino, si ottengono le relazioni

[1] formula

dove β=v/c; le [1] vanno, complessivamente, sotto il nome di trasformazione di Lorentz. Risulta anzitutto da esse che condizione perché la trasformazione sia, come ovviamente è necessario, reale, è che sia β≤1, cioè v≤c: in altri termini la velocità di un corpo (rispetto a un qualsiasi riferimento galileiano) non può mai superare la velocità della luce. Inoltre se c è molto più grande di v, così da potersi considerare β trascurabile rispetto all’unità, le [1] si riducono a:

[2] formula

complessivamente ricordate come trasformazioni di Galileo che forniscono le relazioni intercorrenti fra le coordinate spazio-temporali di un evento misurate dai due osservatori O e O′, ottenibili attribuendo al tempo carattere di grandezza assoluta.

Dalle relazioni generali [1] si deducono, nell’ambito cinematico, tre fatti fondamentali: la r. della contemporaneità, la contrazione delle lunghezze (o contrazione di Lorentz), la dilatazione dei tempi. La r. della contemporaneità consiste in questo: due eventi risultano contemporanei rispetto a due osservatori che si muovano l’uno rispetto all’altro di moto traslatorio rettilineo uniforme soltanto se i due eventi si verificano nello stesso posto. Parlando di contrazione delle lunghezze s’intende in sostanza esprimere il fatto che la lunghezza di un segmento valutata da un osservatore che sia in moto rispetto a essa risulta minore di quella che misurerebbe un osservatore in quiete rispetto al segmento. Precisamente, se AB è un segmento fisso rispetto all’osservatore O ed l ne è la lunghezza misurata da O, la sua lunghezza l′ misurata da O′ vale

[3] formula

Per es., un treno in corsa ha per un osservatore a terra lunghezza minore di quella che gli attribuisce un osservatore che si trovi sul treno. Naturalmente, anche quest’effetto è assolutamente inapprezzabile alle velocità ordinarie, cioè per velocità molto inferiori alla velocità della luce. Invece la durata di un fenomeno misurata da un osservatore in moto risulta maggiore che per un osservatore in quiete. Precisamente, indicando con Δt′ e Δt le due durate, si ha

[4] formula

Anche in questo caso si riconosce che ove sia β≅0 risulta Δt′≅Δt. La sostituzione della trasformazione di Lorentz alla classica trasformazione di Galileo comporta, com’è naturale, modificazioni anche nelle formule che esprimono il principio dei moti relativi, la cui formulazione relativistica ha trovato conferma sperimentale in un’esperienza di A.-H.-L. Fizeau relativa alla determinazione della velocità della luce in un mezzo in moto. In particolare si riconosce che, qualunque siano la velocità relativa e quella di trascinamento (la grandezza delle quali, come s’è già detto, non può mai superare la velocità della luce), anche la velocità assoluta, che si ottiene come risultante delle due, non può mai superare la velocità della luce.

Se dall’ambito cinematico, in cui restano confinate le osservazioni precedenti, si passa alla dinamica, vi è innanzitutto da osservare che l’equazione fondamentale F=ma, invariante rispetto alla trasformazione di Galileo, non resta più tale rispetto alla trasformazione di Lorentz, per cui essa perderebbe il suo carattere di relazione fondamentale se non venisse opportunamente modificata. È in un certo senso l’inverso di ciò che si verifica per le equazioni fondamentali dell’elettromagnetismo, le quali, mentre non sono invarianti rispetto alla trasformazione di Galileo, lo sono invece rispetto a quella di Lorentz, ed è pertanto ragionevole la presunzione di un sostanziale accordo tra i principi posti da Maxwell a fondamento della sua teoria e i principi della relatività. L’adattamento dell’equazione fondamentale della dinamica può essere conseguito ammettendo, anche nell’ambito della meccanica relativistica, la validità del principio di conservazione della quantità di moto (➔ azione).

Nella meccanica relativistica, però, non viene più postulata la costanza della massa. Si riconosce allora, per questa via, che se m₀ è la massa del corpo secondo la meccanica classica, in condizioni di moto deve essergli attribuita una massa m legata a m₀ dalla relazione

[5] formula

In altri termini, si deve distinguere tra la massa di quiete (o di riposo m₀) invariabile e la massa in condizioni di moto, m, detta genericamente massa relativistica, crescente con la velocità. Se la velocità si avvicina a quella c della luce, come può avvenire per determinate radiazioni corpuscolari, la massa relativistica tende a diventare infinitamente grande. Si ha, per es., per gli elettroni costituenti i raggi β emessi dal carbonio radioattivo, v=297.000 km/s; v/c=99/100; m=7,09 m₀; la previsione teorica che la massa relativistica diventi oltre 7 volte la massa di quiete risulta confermata dall’esperienza. Aumento della massa di un corpo significa in definitiva aumento della sua inerzia, cioè della sua riluttanza a cambiare di velocità: cosicché il controllo dell’aumento di massa può essere effettuato attraverso la determinazione della forza che occorre applicare al corpo, dotato di una certa velocità, per provocare in una certa misura un aumento di questa. Ammessa, come teoria ed esperienza portano ad ammettere, la variabilità della massa, la legge fondamentale della dinamica classica va sostituita dalla relazione

[6] formula

dove per m deve ora intendersi la massa relativistica in funzione della velocità espressa dalla [5]. Se si proietta la [6] sulla tangente T e sulla normale principale N alla traiettoria del punto, si ha, ricordando che dv/dt=a_T,

equazioni in cui figurano nella seconda la massa relativistica m, detta perciò anche massa trasversale, e nella prima la massa

[7] formula

che ha invece il nome di massa longitudinale. La [6] mette anche in evidenza che forza e accelerazione non hanno più in generale la stessa direzione e il rapporto F/a dipende dalla direzione della forza. Fanno eccezione i due casi in cui la forza sia parallela oppure perpendicolare alla velocità, per i quali il rapporto F/a risulta rispettivamente uguale alla massa longitudinale o alla massa trasversale. Si può inoltre osservare che anche il teorema dell’energia cinetica resta valido nell’ambito della meccanica relativistica, a patto però di assumere per l’energia cinetica E_c l’espressione relativistica

[8] formula

che per piccole velocità si riduce precisamente all’espressione classica m₀v²/2. Per v tendente a c, E_c tende a diventare infinitamente grande: prima conseguenza di questo fatto è che per portare un corpo dalla quiete alla velocità della luce occorrerebbe compiere un lavoro infinitamente grande; anche da questa circostanza la velocità della luce viene a presentarsi come una velocità limite che nessun corpo materiale può raggiungere, quali che siano le forze su di esso applicate. La [8] può esser scritta nella forma m=m₀+E_c/c², la quale suggerisce un’interpretazione di fondamentale interesse: la massa relativistica di un corpo risulta dalla somma della sua massa di quiete e di un contributo che si può considerare a essa portato dall’energia cinetica, o, in altri termini, all’energia cinetica si può sempre pensare associata una massa pari a E_c/c².

Il discorso che si fa per l’energia cinetica si può ripetere per qualsiasi altra forma di energia (in qualche modo trasformabile in energia cinetica), con la conclusione che a ogni energia E si può pensare associata una massa m=E/c² che è detta massa dell’energia, e viceversa a ogni massa m si può pensare associata un’energia E=mc². In particolare, in condizioni di quiete nelle quali è m=m₀ si dovrà pensare associata alla massa di quiete l’energia m₀c², che è detta energia intrinseca; viceversa: ogni corpo che possiede, sotto qualunque forma, un’energia di riposo E₀, possiede anche una massa di quiete m₀=E₀/c² (principio einsteiniano dell’inerzia dell’energia). Ogni grammo-massa possiede l’enorme energia intrinseca di 9∙10¹³ joule. Così massa ed energia non si presentano più come enti diversi ma come aspetti diversi di uno stesso ente che, a seconda dei casi, macroscopicamente si manifesta come massa o come energia. Segue in particolare il principio della conservazione della massa-energia, secondo il quale per un sistema isolato non si mantengono più separatamente costanti, come nella meccanica classica, la massa e l’energia, bensì la somma delle due (espresse ambedue in termini di massa o in termini di energia). Gli sviluppi della fisica nucleare, confermando il risultato, hanno portato una delle più autorevoli conferme a questo principio.

R. generale

La r. ristretta fondata sul principio che tutti i riferimenti inerziali sono equivalenti per la descrizione dei fenomeni fisici attribuisce a tali riferimenti un privilegio per la formulazione delle leggi naturali, che non hanno tutti gli altri riferimenti, non inerziali. Questo privilegio non è giustificato né da proprietà particolari dei corpi né dal concetto di moto e deve essere considerato come una proprietà dello spazio-tempo. A tale concezione vengono mosse due diverse obiezioni: la prima è che concepire lo spazio-tempo come avente un effetto fisico, senza che su di esso sia possibile agire, è contrario allo sviluppo del pensiero scientifico; la seconda è che nella meccanica newtoniana il rapporto fra le masse di due corpi è definito in due modi profondamente diversi, che portano agli stessi valori numerici, senza però che sia possibile fornire una qualificazione che riconduca a una uguaglianza della reale natura dei due concetti: a) il rapporto fra le masse di due corpi è uguale al rapporto inverso delle accelerazioni impresse ai due corpi da una stessa forza motrice (masse inerziali m_i); b) il rapporto fra le masse di due corpi è uguale al rapporto fra le forze che agiscono sui due corpi nello stesso campo gravitazionale (masse gravitazionali m_g). Questi due procedimenti, concettualmente differenti, hanno dato luogo a esperienze di grandissima precisione, eseguite da R. Eötvös, che hanno fornito gli stessi valori numerici. Affermare che la massa inerziale è uguale alla massa gravitazionale, in base alle esperienze di Eötvös equivale ad affermare che l’accelerazione impressa a un corpo da un campo gravitazionale è indipendente dalla natura del corpo. Infatti per l’equazione newtoniana di moto di un corpo in un campo gravitazionale si ha:

[9] formula

Le considerazioni critiche ora accennate indussero Einstein ad ampliare la validità del principio di r. già enunciato a fondamento della r. ristretta. Se si considera un riferimento inerziale K, le masse che sono sufficientemente lontane l’una dall’altra, e da ogni altro corpo, non hanno accelerazione alcuna rispetto al riferimento K. Se le masse suddette sono esaminate da un altro riferimento K′, dotato di moto traslatorio rettilineo uniformemente accelerato rispetto a K, si sa che esse hanno accelerazioni tutte vettorialmente uguali: ossia si comportano come se K′ non fosse in moto traslatorio accelerato, ma fosse presente in esso un campo gravitazionale. Lasciando da parte per qualche istante la causa di tale campo gravitazionale, nulla impedisce di supporre reale tale campo e il riferimento K′ in quiete. Si è così naturalmente condotti ad affermare il principio generale di r.: «tutte le leggi fisiche possono essere formulate in modo formalmente identico in ogni riferimento fisico, purché si tenga conto della distribuzione e del moto della materia dell’Universo rispetto al riferimento medesimo».

Questo principio è connesso intimamente con il principio di equivalenza che afferma l’uguaglianza fra massa inerziale e massa gravitazionale. Difatti le stesse masse appaiono soggette alla sola inerzia rispetto al riferimento K, e all’azione congiunta dell’inerzia e della gravitazione rispetto al riferimento K′. Si perviene così a unificare la natura della massa e della gravitazione. Come si vede immediatamente con alcuni semplici esempi, il campo gravitazionale (che localmente è equivalente a un campo di accelerazioni) influenza e determina le leggi metriche dello spazio-tempo (in presenza di un campo gravitazionale la geometria non è euclidea). Sia infatti K′ un riferimento fisico rotante uniformemente attorno a un asse z solidale con un riferimento inerziale K, se, per esempio, si considera un cerchio con centro sull’asse z appena scelto, posto in un piano ortogonale all’asse z medesimo, in quiete nel riferimento K′ e si immagina di disporre di un gran numero di campioni di lunghezza tutti uguali fra loro, si può supporre di misurare il contorno e il diametro del cerchio in due modi diversi: una volta con il riferimento K′ in quiete rispetto al riferimento K, una seconda volta col riferimento K′ uniformemente rotante rispetto a K. Indicati con u e d il numero di campioni disposti per misurare rispettivamente la circonferenza e un diametro, si ottiene nel primo caso u/d=π. Nel secondo caso, supponendo di determinare, a un certo istante nel riferimento K, la posizione dei punti terminali di tutti i campioni di lunghezza disposti lungo la circonferenza e lungo il diametro scelto, si trova che tutti i campioni disposti lungo la circonferenza subiscono la contrazione di Lorentz, mentre quelli disposti lungo il diametro non subiscono tale contrazione (nel senso della loro lunghezza). Perciò risulta ora u/d>π. Le leggi geometriche valide nel riferimento K′, per un osservatore posto in K, non sono pertanto in accordo con la geometria euclidea. Inoltre, se due orologi simili sono posti in K′, l’uno al centro del cerchio, l’altro in un punto della circonferenza, e sono sincronizzati a un dato istante di K, essi, visti dal riferimento K, indicheranno tempi diversi: quello che è al centro avanzerà più rapidamente di quello che è sulla circonferenza. Si perviene così al risultato seguente: lo spazio e il tempo non possono essere definiti rispetto al riferimento K′ come lo erano nei riferimenti inerziali in r. ristretta. D’altra parte deve sussistere il principio di equivalenza, e il riferimento K′ deve poter essere considerato come un riferimento in quiete nel quale vi sia un campo gravitazionale.

Considerazioni di questo tipo, il principio generale di r. e la teoria riemanniana delle varietà (➔ Riemann, Bernhard) suggerirono a Einstein di interpretare gli effetti della gravitazione come una modificazione della struttura geometrica dello spazio-tempo: la struttura geometrica dell’Universo non è euclidea, ma è determinata dalla distribuzione delle masse; in prossimità di quest’ultime lo spazio si curva trasformandosi da euclideo a uno spazio riemanniano. In tale spazio le linee geodetiche, ovvero le linee più brevi congiungenti due punti, sono curve e la loro forma è determinata dal campo gravitazionale. E infatti una delle verifiche sperimentali classiche della r. generale riguarda la deflessione subita dai raggi luminosi, provenienti da stelle, quando passano nel campo gravitazionale del Sole.