neutrino

Particella elementare elettricamente neutra, con spin 1/2 (in unità ℏ) e massa nulla o comunque al disotto delle capacità attuali di misurazione, appartenente alla famiglia dei leptoni.

Fisica

Tipi di neutrini

Esistono tre tipi di n., indicati con i simboli ν_e, ν_μ, ν_τ, e tre tipi di corrispondenti antiparticelle (antineutrini), ν̄_e, ν̄_μ, ν̄_τ, che si diversificano dai n. per avere numero leptonico opposto (➔ particelle elementari). I n. interagiscono con la materia solo median;te le interazioni deboli e quindi possono attraversare indisturbati enormi spessori di qualsiasi materiale (il che rende molto problematica la loro rivelazione). L’ipotesi dell’esistenza del n. è stata avanzata da W. Pauli nel 1931 per spiegare lo spettro continuo di energia degli elettroni nel decadimento β; nella teoria di E. Fermi formulata nel 1934, il decadimento β di un nucleo è interpretato come dovuto alla reazione n → p + e + ν̄_e che ha luogo anche per neutroni liberi. Un nucleo può anche decadere emettendo un e⁺ e questo processo è interpretato come dovuto alla reazione p → n + e⁺ + ν_e, che può aver luogo solo in protoni legati nel nucleo (essendo la massa del neutrone maggiore di quella del protone). Le stelle, nelle quali in ogni ciclo protone-protone sono prodotti due e⁺ e due ν_e, sono sorgenti intensissime di ν_e. I reattori nucleari, nei quali la reazione di fissione produce frammenti nucleari e neutroni liberi soggetti al decadimento β, sono sorgenti di flussi intensi di antineutrini ν_e. L’esisten;za dei n. (più precisamente di antineutrini) fu confermata da un esperimento eseguito nel 1956 da C. Cowan, F. Reines, F.B. Harrison, H.W. Kruze e A.D. McGuire.

L’esistenza di un secondo n., il ν_μ, fu ipotizzata da B. Pontecorvo e altri in connessione con i decadimenti del muone e del pione. Il n. ν_μ (o l’antineutrino ν̄_μ) è emesso in decadimenti in cui interviene il muone, in particolare in quelli del μ medesimo: μ^– → e + ν̄_e+ν_μ; μ⁺→e⁺+ν_e+ν̄_μ; π^–→μ^–+ν̄_μ; π⁺→μ⁺+ν_μ ecc.

Il terzo n., il ν_τ, è stato introdotto nel 1975 in seguito alla scoperta del leptone τ. Il n. ν_τ (o l’antineutrino ν̄_τ) è emesso in decadimenti in cui interviene il leptone τ, in particolare in quelli del τ medesimo: τ^–→μ^–+ν̄_μ+ν_τ; τ^–→e^–+ν̄_e+ν_τ; τ^–→π^–+ν_τ; τ⁺→μ⁺+ν_μ+ν̄_τ ecc. Del ν_τ non si sono avute osservazioni dirette.

La massa dei neutrini

Non sembrano esservi ragioni teoriche di principio che comportino massa rigorosamente nulla per i neutrini. È quindi in corso un intensivo e diversificato sforzo sperimentale per evidenziare un’eventuale massa non nulla dei n.; la scoperta che i n. hanno massa non nulla avrebbe grande importanza non solo per la fisica delle particelle ma anche per l’astrofisica e la cosmologia: n. massivi potrebbero infatti risolvere il problema della cosiddetta massa mancante nell’Universo, cioè del fatto che la massa presente sotto forma di materia ‘visibile’ nell’Universo, e anche negli ammassi di galassie e nelle singole galassie, non è sufficiente a spiegarne l’evoluzione osservata. La materia oscura costituita dai n. massivi potrebbe ‘chiudere’ l’Universo, cioè far sì che all’attuale fase di espansione dell’Universo ne segua una di contrazione oppure, come preferito dalle moderne teorie dell’inflazione cosmica, che si realizzi la soluzione limite che separa l’Universo aperto dall’Universo chiuso. Un limite superiore sulla massa del ν_e si ottiene studiando lo spettro energetico dell’elettrone emesso nel decadimento β, in particolare misurando il valore massimo dell’energia dell’elettrone nel sistema di quiete del nucleo che decade. In pratica si usa il decadimento β del trizio (³H→³He+e+ν_e) e il limite superiore sulla massa del ν_e così ottenuto è 7,3 eV/c², ovvero il ν_e è almeno settantamila volte meno massivo dell’elettrone. I limiti sulle masse del ν_μ e del ν_τ sono molto meno stringenti: il valore attuale del limite superiore sulla massa del ν_μ è 270 keV/c²; il limite superiore sulla massa del ν_τ, è 31 MeV/c².

Oscillazioni dei neutrini

Fenomeno ipotizzato da B. Pontecorvo nel 1968 che avrebbe luogo solo se le masse dei n. fossero diverse tra loro (e quindi necessariamente non tutte nulle), consistente in una variazione sinusoidale con la distanza percorsa del contenuto in ν_e, ν_μ e ν_τ di un fascio di n. inizialmente composto da n. tutti dello stesso tipo. I n. oscillerebbero nel senso che dato, per es., un fascio di ν_μ prodotto nel decadimento in volo di pioni, la composizione di questo fascio dovrebbe variare con legge sinusoidale in funzione della distanza dal luogo di produzione: se inizialmente fossero presenti solo ν_μ, questi nel loro moto dovrebbero trasformarsi in ν_e e ν_τ e questi a loro volta, successivamente, gli uni negli altri e in ν_μ, e così via. La scoperta di oscillazioni sarebbe possibile soltanto se i n. (o almeno un solo tipo di n.) avessero una massa diversa da zero, consentendo così di misurare il valore della differenza di massa tra i due tipi di n. oscillanti. Gli esperimenti fino a ora eseguiti hanno dato, nei limiti degli errori, risultati negativi.

Astronomia

Le sorgenti di n. nell’Universo

Nell’Universo, i n. sono prodotti in moltissimi processi: per es., nelle reazioni termonucleari che avvengono nell’interno del Sole e delle altre stelle, e nei collassi stellari che danno luogo alle esplosioni di supernovae. L’interesse in astronomia per la rivelazione dei n. extraterrestri sta soprattutto nel fatto che essi possono giungere fino a noi da regioni dell’Universo che altrimenti sarebbero inaccessibili all’osservazione. Mentre, per es., la radiazione elettromagnetica prodotta nelle reazioni nucleari che avvengono in una stella non riesce a filtrare attraverso gli strati esterni dell’astro, i n., che interagiscono molto debolmente con la materia, sfuggono in gran parte, disperdendosi nello spazio. Il flusso di n. proveniente da sorgenti celesti (primariamente il Sole) che giunge sulla Terra è imponente: oltre 1000 miliardi di particelle per centimetro quadrato e per secondo. È però assai difficile rivelare queste particelle, proprio perché la loro sezione d’urto è piccolissima. Il Sole (per la sua vicinanza) e le supernovae (per l’enorme quantità dell’energia liberata) rimarranno, ancora per molti anni, le uniche sorgenti di n. osservabili.

N. solari

fig. 1

Previsioni teoriche

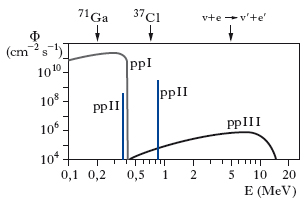
L’energia solare è prodotta dalla fusione nucleare dell’idrogeno in elio. Questo processo può compiersi attraverso due cicli diversi di reazioni (➔ Sole), detti rispettivamente ciclo CNO e ciclo protone-protone (più brevemente, ciclo p-p). Quest’ultimo ciclo si articola, a sua volta, in tre catene di reazioni, dette ppI, ppII e ppIII. Secondo la teoria correntemente accettata (il cosiddetto modello solare standard), nelle condizioni esistenti nel nucleo del Sole, il ciclo p-p dovrebbe essere largamente dominante su quello CNO, che contribuirebbe soltanto per l’1% alla produzione totale di energia. D’altra parte, nell’ambito del ciclo p-p, la catena di reazioni più efficace sarebbe la ppI, che da sola produrrebbe oltre il 90% dell’energia solare. I processi precedenti hanno una caratteristica in comune: infatti, quale che sia il ciclo di reazioni attraverso cui avviene la fusione dell’idrogeno, la produzione di ciascun nucleo di elio si accompagna sempre allo sviluppo di due n. del tipo ν_e. Il flusso dei n. che esce dal Sole può allora essere calcolato in un modo molto semplice e scevro da ambiguità. Poiché il Sole irradia ogni secondo un’energia di 4∙10²⁶ J=2,5∙10³⁹ MeV, e nella formazione di ciascun nucleo di elio si libera un’energia di 26,7 MeV, ogni secondo devono prodursi ∿10³⁸ nuclei di elio e, quindi, ∿2∙10³⁸ neutrini. D’altra parte, l’energia posseduta dai n. dipende fortemente dalle particolari reazioni in cui essi sono generati: per es., i n. della catena ppIII sono più energetici di quelli della catena ppII. Per determinare la distribuzione di energia dei n. occorre allora conoscere l’efficienza delle varie catene di reazioni, che può essere prevista in base al modello solare standard. La fig. 1dà il numero di n. che dovrebbe incidere ogni secondo su ogni metro quadrato di una superficie normale al segmento distanza Sole-Terra alla distanza della Terra, in funzione della loro energia (per semplicità, si sono considerate solo le reazioni più rilevanti).

Confronto con le osservazioni

I dati provenienti dai vari esperimenti ideati per la misura dei n. rivelano un flusso di n. solari inferiore a quello previsto teoricamente. Questa discrepanza fra le aspettative teoriche e i risultati delle misure sperimentali costituisce il problema dei n. solari. La soluzione del problema può essere ricercata sia nell’ambito dell’astrofisica sia in quello della fisica delle particelle elementari. La prima strada conduce a una revisione del modello solare standard e, quindi, dell’intera teoria della struttura solare accettata. In particolare, se la temperatura centrale del Sole fosse più bassa di quella attesa, il flusso di n. solari si ridurrebbe sensibilmente: data la scarsa plausibilità delle teorie basate su questa ipotesi, ci si è orientati a trovare la soluzione del problema dei n. nell’ambito della fisica della propagazione di queste particelle. Infatti, se i n. oscillassero fra i tre stati ν_e, ν_μ e ν_τ, come proposto da B. Pontecorvo, il flusso dei n. ν_e (gli unici praticamente rivelabili) si ridurrebbe sostanzialmente e la discrepanza verrebbe sanata. Va tuttavia sottolineato che l’ipotesi dell’oscillazione del n. non è stata provata sperimentalmente, sicché il problema dei n. solari rimane aperto. Concludendo, notiamo che le osservazioni dei n. hanno già dato un contributo importante alla conoscenza del Sole, in quanto hanno confermato che questo, in accordo con le aspettative teoriche, deve ricavare la massima parte della sua energia dalle reazioni del ciclo p-p. Infatti, se il ciclo CNO fosse predominante, il flusso di n. energetici sarebbe assai più grande e la discrepanza fra previsioni teoriche e misure non si potrebbe risolvere nemmeno invocando le oscillazioni dei neutrini.

N. dalle supernovae

Previsioni teoriche

Le stelle aventi massa maggiore di ∿10M_⊙ (dove M_⊙ è la massa del Sole), quando nel loro interno si sono esaurite le reazioni nucleari, vanno incontro a un collasso catastrofico (➔ stella). L’esplosione che segue, nella quale gran parte della stella va distrutta, prende il nome di supernova, più precisamente di supernova di Tipo II. Si calcola che in una tipica esplosione di supernova venga liberata, in pochi secondi, un’energia di oltre 10⁴⁶ J (per confronto, il Sole, bruciando nel corso di ∿10 miliardi di anni tutto l’idrogeno disponibile, svilupperà complessivamente un’energia di ∿10⁴⁴ J). La massima parte di questa energia (forse il 99%) verrebbe trasportata nello spazio da un flusso di ∿10⁵⁷ n. (ν_e, ν_μ, ν_τ e ν̄_e, ν̄_μ, ν̄_τ). L’energia media dei n. sarebbe dell’ordine di 10 MeV.

fig. 2

L’osservazione dei n. della supernova SN1987A

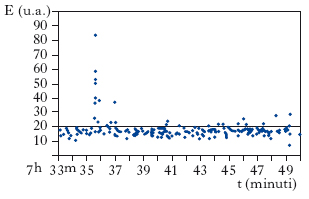
Gli unici n. di origine non solare che finora siano stati rivelati sono quelli prodotti dalla supernova SN1987A, osservata il 23 febbraio 1987. L’esplosione è avvenuta in una galassia vicina alla Via Lattea, la Grande Nube di Magellano, situata a una distanza di ∿55 kpc dalla Terra. Due esperimenti hanno osservato con certezza n. provenienti da questa sorgente: Kamiokande 2 (esperimento giapponese), che ne ha contati ∿12, e IMB (esperimento statunitense), che ne ha contati ∿8. La fig. 2mostra i segnali registrati da Kamiokande, intorno alle 7^h35^m (tempo universale) del 23 febbraio 1987: l’addensarsi di una decina di eventi significativi (cioè al di sopra della linea tratteggiata che indica il rumore di fondo dell’esperimento) in un intervallo di tempo brevissimo garantisce che i n. osservati provengano effettivamente dalla supernova (i n. solari sono infatti rivelati alla media di uno ogni tre giorni). Tuttavia, l’interpretazione dei dati raccolti non è priva di incertezze.