quark

Termine formato da qu(estion m)ark, «punto interrogativo», usato come parola di significato indeterminato da J. Joyce nella frase three quarks for Muster Mark del romanzo (1939) Finnegan’s Wake.

In fisica, i q. sono le particelle costituenti gli adroni, cioè le particelle soggette a interazione forte (➔ forti, interazioni). Introdotti da M. Gell-Mann e G. Zweig (1964) per spiegare la proliferazione degli adroni e alcune regolarità in essa riscontrate, si sono rivelati di fondamentale importanza per la comprensione della fisica delle particelle elementari e sono un ingrediente essenziale del cosiddetto Modello Standard (➔ particelle elementari). Si conoscono 6 tipi distinti di q. (si parla convenzionalmente di q. con 6 distinti sapori o flavours), i q. up, down, strange, charme, beauty e top (indicati rispettivamente con i simboli u, d, s, c, b, t). Di ciascuna di queste 6 particelle si hanno tre repliche diverse caratterizzate da una grandezza denominata convenzionalmente colore o carica di colore (in tal senso si parla di q. colorati). I q. hanno spin 1/2 (in unità di ℏ), carica elettrica +2/3 o −1/3 (in unità di carica del protone) e numero barionico 1/3. Dal momento che non sono mai stati osservati q. liberi, vale a dire al di fuori degli adroni, si è giunti, confortati dai risultati della cromodinamica quantistica (➔ forti, interazioni), alla conclusione che i q. sono confinati negli adroni da mutue forze attrattive che non decrescono con la distanza.

I q. e la classificazione degli adroni

Alla fine degli anni 1940 gli unici adroni noti erano il nucleone e il pione. A partire dagli anni 1950, grazie alle ricerche condotte con i raggi cosmici e con macchine acceleratrici che consentivano di raggiungere energie sempre più elevate (e quindi, per l’equivalenza massa-energia, di produrre particelle con masse sempre maggiori) e di rivelatori sempre più sofisticati, si è avuta una vera e propria proliferazione degli adroni prima con la scoperta delle particelle strane e successivamente di vari stati eccitati degli adroni già osservati. All’inizio degli anni 1960 erano infatti stati osservati 8 barioni con spin 1/2 e 9 con spin 3/2, 8+1 mesoni con spin 0 e 8+1 con spin 1. A causa dell’invarianza delle interazioni forti per rotazioni nello spazio dello spin isotopico (I) era chiaro che i vari stati di carica di un adrone (costituenti un multipletto di spin isotopico) dovevano essere considerati come stati (caratterizzati da differenti valori della terza componente dello spin isotopico I₃) di una medesima particella.

fig. 1

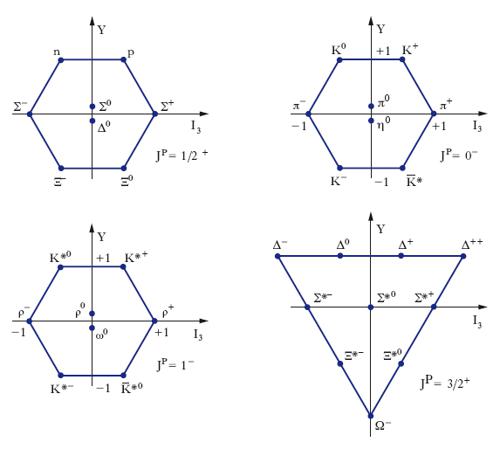
Sorse allora spontanea la domanda se esistessero altri schemi, di portata più ampia, capaci di inquadrare in modo semplice un maggior numero di particelle. Questo problema fu affrontato con un approccio sviluppato a partire dal 1961 indipendentemente da M. Gell-Mann e Y. Ne’eman, basato sulla teoria dei gruppi. Essi osservarono che se si trascurano, entro certi limiti, le differenze di massa degli adroni dotati degli stessi valori di numero barionico (A), spin (J) e parità (P) si ottengono supermultipletti, composti a seconda dei casi di 8 o 10 membri, e singoletti, le cui proprietà sono descritte in modo completo dalle rappresentazioni del gruppo di Lie SU(3). Se infatti si rappresenta ciascun membro di un supermultipletto con un punto in un piano (I₃, Y), dove Y=A+S è l’ipercarica (data dalla somma del numero barionico A e della stranezza S), si ottengono le strutture riportate in fig. 1 che riproducono le diverse rappresentazioni del gruppo SU(3). Si riuscì inoltre a stabilire una relazione che forniva le differenze di massa delle particelle di un supermultipletto. Tra i vari successi di questo approccio basta ricordare, per es., che per completare il decupletto barionico con J^P=(3/2)⁺ Gell-Mann predisse l’esistenza dell’Ω^–, fissando non solo i valori dei corrispondenti numeri quantici ma anche il valore della sua massa; poco dopo l’Ω^– fu osservato sperimentalmente.

fig. 2

fig. 3

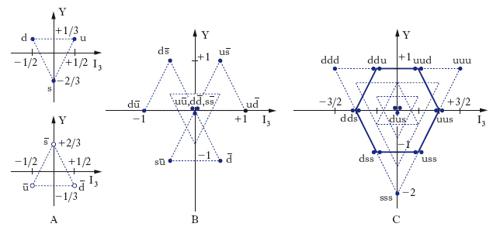
La scoperta che gli adroni potevano essere descritti come supermultipletti di SU(3) può essere paragonata, sotto molti punti di vista, alla scoperta fatta da D.I. Mendeleev nel 1869 del sistema periodico degli elementi: si tratta in entrambi i casi di scoperte fondamentali, di natura puramente fenomenologica, le quali suggeriscono che gli enti fisici per i quali si è constatata una semplice regola classificatoria possiedano una struttura interna che giustifichi le regolarità osservate. Poiché tutte le rappresentazioni di un gruppo di Lie possono essere costruite combinando in modo opportuno un adeguato numero di rappresentazioni di minima dimensionalità (nel caso di SU(3) il valore minimo delle dimensioni è 3), nel 1964, indipendentemente, Gell-Mann e Zweig proposero di attribuire un significato concreto agli stati corrispondenti alle rappresentazioni di SU(3) di minima dimensionalità, ipotizzando che tutti gli adroni fossero aggregati di tre diversi tipi di particelle fondamentali (e delle rispettive antiparticelle), costruiti in modo tale che l’invarianza rispetto a SU(3) risultasse automaticamente rispettata. I mattoni fondamentali di questa costruzione furono chiamati q. da Gell-Mann (fig. 2). In fig. 3 è riportata la composizione in q. di alcuni adroni.

Il modello a q., nato da esigenze classificatorie, fu sviluppato per dar conto di tutte le proprietà degli adroni e ha via via ricevuto notevoli conferme sperimentali. Per spiegare alcune anomalie riscontrate sul piano teorico e le proprietà di nuove particelle scoperte nel frattempo, accanto ai tre q. u, d (componenti dei nucleoni) e s (componente delle particelle strane, dotato del numero quantico stranezza, ingl. strangeness) sono stati successivamente introdotti i q. c, b, t (di quest’ultimo, previsto sulla base di molte indicazioni teoriche, si sono avute le prime conferme sperimentali solo a partire dal 1994), dotati di nuovi numeri quantici di sapore chiamati rispettivamente charm («fascino»), beauty («bellezza») o bottomness, truth («verità») o topness e indicati con i simboli C, ℬ, T. Con l’introduzione dei q. c, b, t (detti anche q. pesanti, in contrapposizione ai q. leggeri u, d, s) aumenta enormemente il numero di particelle elementari (adroni) che possono essere classificate con il modello a quark.

Il mesone costituito da un q. pesante (c, t, b) e dal corrispondente antiquark è chiamato quarkonio: esempi di quarkonio sono il charmonio, il toponio ecc.

Considerando gli adroni come stati legati di q. (i barioni di tre q., i mesoni di un q. e di un antiquark) era possibile spiegare le loro proprietà, ma fu ben presto evidente che i q. dovevano possedere un ulteriore numero quantico interno (oltre quelli sopra indicati) che fu chiamato colore; in primo luogo, per far sì che nel barione Δ⁺⁺ i tre q. u potessero (attribuendo loro 3 colori diversi) soddisfare il principio di Pauli pur avendo gli spin paralleli e funzione d’onda spaziale simmetrica. Poiché questo nuovo grado di libertà non si manifestava a livello adronico, si ritenne che ogni adrone dovesse essere globalmente privo di colore (in particolare che i 3 q. di un barione dovessero avere colore diverso).

Ogni q. in un adrone dà luogo a una nube di gluoni e di coppie q.-antiquark virtuali, e si è soliti distinguere tra q. vestiti e q. nudi, cioè comprensivi o meno di detta nube. Un adrone è quindi costituito da 2 o 3 q. vestiti ma da infiniti q. e antiquark nudi e gluoni. Poiché indicazioni teoriche suggeriscono che a ciascuna coppia di leptoni (e, ν_e), (μ, ν_μ), (τ, ν_τ) debba corrispondere una coppia di q. rispettivamente con carica 2/3 e −1/3, e poiché misure di grande precisione della ‘larghezza’ della Z⁰ hanno escluso che esistano più di 3 coppie di leptoni, le 3 coppie di q. (u, d), (c, s), (t, b) dovrebbero esaurire tutti i quark.

I q. e la struttura dei nucleoni

L’evidenza della struttura a q. degli adroni è fornita, oltre che dal successo conseguito nella loro classificazione e nello studio delle loro interazioni, da un gran numero di prove sperimentali dirette e ottenute dallo studio dei processi di diffusione anelastica con alto trasferimento di energia e di quantità di moto (diffusione anelastica profonda, ingl. deep inelastic scattering) leptone-nucleone, in quanto in questi processi i nucleoni rivelano una struttura interna assimilabile a un gas di particelle puntiforni (che vengono indicate genericamente come partoni). Tutti i risultati sono in accordo con l’ipotesi secondo la quale i partoni carichi siano q. e che il protone sia costituito da tre q. vestiti, ciascuno circondato da una nube di infiniti q. e antiquark nudi. Inoltre danno conferma al fatto che un nucleone è costituito da tre q. vestiti (cioè da 3 q. nudi e da un mare di coppie q.-antiquark anch’essi nudi).

Le interazioni tra quark

La teoria che descrive le interazioni tra q. colorati, la cromodinamica quantistica, è basata sull’idea che le cariche di colore siano le sorgenti di un campo di forze (il campo gluonico) mediato da 8 gluoni, con massa nulla, spin 1 e dotati di carica di colore. È una teoria di campo relativistica e quantistica con interazioni locali. Le interazioni tra q. colorati sono generate dallo scambio di gluoni, in analogia con le interazioni fra cariche elettriche, dovute allo scambio di fotoni. Esiste però una differenza sostanziale tra gluoni e fotoni: questi ultimi sono elettricamente neutri e quindi non possono accoppiarsi reciprocamente, ovvero un fotone non può dar luogo a più fotoni. I primi invece (sebbene sempre elettricamente neutri) sono dotati di carica di colore e questo permette loro di avere interazioni mutue. Le cariche elettriche si possono tutte esprimere in funzione di una carica di riferimento, convenzionalmente scelta come quella dell’elettrone. Di cariche di colore fondamentali invece ne esistono 3, identificate con le possibili cariche di un quark. Se chiamiamo rosso, giallo e blu i tre ‘colori’ fondamentali, i possibili stati di colore di un gluone si possono collegare alle scelte di coppie dei colori fondamentali. In linguaggio matematico, i gluoni sono associati ai generatori del gruppo detto SU(3) di colore e sono 8.

La cromodinamica quantistica, così come l’elettrodinamica quantistica, appartiene a una vasta classe di teorie dotate di invarianza di gauge. Questa permette di scegliere in modo indipendente in ogni punto dello spazio il sistema di riferimento rispetto al quale vengono definiti gli elementi del gruppo di simmetria. Nel caso del colore l’invarianza di gauge permette di cambiare il colore associato a ogni punto dello spazio tempo. Essa si realizza introducendo dei campi che trasmettono l’informazione sulle possibili ridefinizioni del colore tra punti vicini: la loro presenza costituisce anche l’interazione tra punti vicini, che quindi deriva da un’esigenza d’invarianza. Tali campi sono quelli dei fotoni per le interazioni elettromagnetiche e dei gluoni per quelle forti. La caratteristica dei gluoni di possedere una carica di colore ne differenzia la dinamica rispetto a quella delle più note interazioni elettromagnetiche. La proprietà più importante che ne deriva è quella del ‘confinamento’ delle cariche di colore. Esse non possono propagarsi nello spazio come quelle elettromagnetiche, ma sono costrette a unirsi ad altre cariche per formare stati legati che abbiano complessivamente carica di colore nulla, ovvero restino invariati per una scelta arbitraria del sistema di riferimento del colore. Questi stati composti possono propagarsi liberamente nello spazio: essi costituiscono l’insieme delle particelle che possono avere interazioni forti. La loro struttura in termini di q. e gluoni si rivela solo a distanze dell’ordine del fermi: a distanze di qualche fermi, grandi rispetto a quelle a cui si legano q. e gluoni, la forza dell’interazione risulta indebolita ma ancora abbastanza potente da legare protoni e neutroni all’interno dei nuclei. A distanze ancora più grandi, dove lo schermaggio delle diverse cariche di colore diventa più efficace, essa scompare del tutto. Anche a distanze inferiori a una frazione di fermi (1 fm = 10^-15 m) le cariche di colore hanno interazioni reciproche sempre più deboli: tale proprietà, comune a tutte le teorie di gauge non abeliane, viene chiamata libertà asintotica.

Lo schermaggio viene operato dai gluoni che vengono prodotti nel vuoto dalle fluttuazioni quantistiche. A corte distanze, infatti, e per tempi estremamente brevi il principio d’indeterminazione sancisce l’impossibilità di avere valori d’impulso ed energia definiti, che invece possono fluttuare, a distanze di un decimo di fermi, fino a valori dell’ordine di un paio di volte la massa del protone. Tali energie vengono convertite in gluoni che schermano la carica di colore e diminuiscono l’intensità dell’interazione. Questo comportamento è dovuto alla presenza di accoppiamenti reciproci tra i gluoni che permettono la conversione di un gluone non solo in una coppia q.-antiquark ma anche in una coppia di gluoni. Esso ancora una volta differisce completamente da quello delle cariche elettriche che invece a corte distanze diventano più intense a causa della conversione dei fotoni solamente in coppie di elettroni-positroni. L’effetto delle fluttuazioni quantistiche può essere espresso attraverso una costante d’accoppiamento efficace, funzione della distanza d, la cui forma esplicita è del tipo:

g²_efficace(d)=costante/ln(1/L²d²).

Il suo valore dipende dal parametro L che quindi fissa la scala delle interazioni forti. Il valore misurato è circa 1/5 della massa del protone. Al diminuire della distanza la costante d’accoppiamento efficace tende a zero logaritmicamente. L’espressione per g²_efficace rappresenta un’approssimazione valida solo per distanze sufficientemente piccole, minori di un decimo di fermi. A distanze più grandi g²_efficace diventa dell’ordine dell’unità e le stime analitiche del suo comportamento diventano inaffidabili. La conoscenza teorica attuale della forza d’interazione tra cariche di colore a distanze dell’ordine del fermi (detta di confinamento) è basata su simulazioni numeriche della teoria; con tali metodi si può calcolare il potenziale esistente tra una coppia q.-antiquark. Si trova che a piccola distanza il potenziale è coulombiano, ovvero simile a quello esistente tra due cariche elettriche: a distanze di circa mezzo fermi s’instaura un nuovo regime nel quale il potenziale cresce linearmente con la distanza di separazione tra le cariche. Questo comportamento implica l’impiego di un’energia infinita per poter allontanare indefinitamente e quindi isolare le cariche di colore e ne determina il confinamento. I calcoli teorici della dinamica dei gluoni indicano che il loro effetto di schermo è funzione della temperatura.

Ad altissime temperature, pari a 10¹⁸ K, la materia adronica subisce una transizione di fase detta di deconfinamento: nella nuova fase il potenziale non cresce più linearmente con la distanza e le cariche di colore isolate, che nella fase fredda hanno una libertà di movimento dell’ordine dei decimi di fermi, possono liberamente propagarsi nella regione di spazio ad alta temperatura. Tramite collisioni di ioni pesanti ad alta energia i fisici sperimentali cercano di riprodurre in laboratorio le condizioni necessarie alla creazione di questo nuovo stato della materia adronica chiamato plasma di q. e gluoni.

Le simulazioni su elaboratore della cromodinamica quantistica predicono anche l’esistenza di stati caratteristici formati da soli gluoni detti glueballs, cioè «palle di colla». La teoria ne prevede parecchi con masse da una volta e mezzo quella del protone a circa 3 volte. L’esistenza del confinamento di stati legati o del plasma ad alta temperatura è manifestazione degli effetti collettivi dei campi generati da molti gluoni in interazione forte tra di loro. A piccole distanze, invece, i gluoni hanno interazioni relativamente deboli con altre cariche di colore a causa del comportamento della costante d’accoppiamento efficace e se ne possono individuare gli effetti che li identificano come particelle elementari. Il loro ruolo individuale all’interno degli adroni si può mettere in evidenza mediante lo studio delle collisioni anelastiche profonde elettrone-nucleone. I q., oltre alle interazioni di colore, sono soggetti, come visto sopra, anche alle interazioni elettromagnetiche e deboli. Nelle interazioni deboli il sapore non si conserva, cioè si può avere la conversione di un q. di un dato sapore in un q. di un altro sapore.