paradosso

Affermazione, proposizione, tesi, opinione che, per il suo contenuto o per la forma in cui è espressa, appare contraria all’opinione comune o alla verosimiglianza e riesce perciò sorprendente o incredibile. Il termine fu usato già dagli stoici, per designare quelle tesi, specialmente etiche, che apparivano contrastanti con l’esperienza comune (per es., che il dolore non fosse un male); Paradoxa stoicorum è il titolo di un’opera di Cicerone (46 a.C.).

Oggi la parola può essere adoperata in senso oggettivo o soggettivo. In senso oggettivo, si denomina p. una tesi che sembra contraddire l’opinione comune o i principi generali di una scienza, ma che, all’esame critico, si dimostra valida; di questo tipo è, per es., il p. idrostatico; o, al contrario, una dimostrazione che, partendo da un presupposto falso e condotta con apparente rigore logico, si risolve definitivamente in un sofisma: erano tali, per es., gli argomenti arrecati da Zenone di Elea contro la molteplicità e il movimento, e sono tali alcuni p. della matematica. In senso soggettivo, il p. è un’affermazione vera o falsa, ma comunque presentata in forma tale da sorprendere il lettore o l’uditore.

Biologia

Effetto paradossale In biologia, il risultato della somministrazione di sostanze quando è opposto a quello che si potrebbe prevedere; per es. quando, somministrando alte dosi di ormone femminile a girini anfibi, se ne ottiene la mascolinizzazione.

Economia

P. del liberale paretiano Teorema presentato dall’economista indiano A.K. Sen (1970) con il quale si vuole dimostrare come, nell’ambito della teoria delle scelte collettive, sia impossibile trovare regole capaci di soddisfare simultaneamente sia il criterio paretiano (secondo cui, data una coppia di alternative possibili, la decisione della collettività deve rispettare l’eventuale unanimità espressa su una delle due) sia il principio del liberalismo individuale (che riconosce ai singoli la possibilità di scegliere alternative diverse o contrarie a quelle collettive).

P. del risparmio Enunciato secondo cui, in una situazione di non piena occupazione e di scarso stimolo agli investimenti, l’aumento della propensione individuale al risparmio determina, attraverso la diminuzione della domanda globale, un minore livello del risparmio aggregato.

P. del valore Proposizione enunciata dall’economista classico A. Smith (1776) che evidenzia come in generale i beni di prima necessità (acqua, aria ecc.) abbiano un valore di scambio notevolmente inferiore rispetto a quello di beni non indispensabili alla vita dell’uomo (oro, diamanti ecc.) a causa della maggiore scarsità e dunque della maggiore utilità marginale associata a questi ultimi.

Fisica

fig.

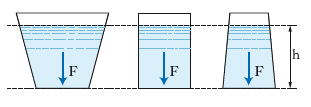
P. idrostatico Quello per il quale se recipienti di forme diverse, ma di ugual base, contengono quantità diverse di un medesimo liquido, che raggiungono però in tutti la medesima altezza h (v. fig.), la forza F che si esercita sul fondo è in tutti la stessa, malgrado la diversità di massa liquida contenuta nei vari recipienti. Il fatto si spiega osservando che tale forza F, risultante delle sole pressioni sul fondo, non coincide – a meno che il recipiente non abbia forme speciali (per es. cilindrica) – con il peso del liquido; quest’ultimo è invece eguale al risultante dei componenti verticali delle forze di pressione esercitate dal liquido contro tutte le pareti del recipiente.

P. degli orologi Ragionamento dal quale sembra emergere una contraddizione nella teoria della relatività ristretta. Uno dei principi fondamentali della teoria afferma (➔ relatività) l’equivalenza tra i sistemi di riferimento inerziali; dalla stessa teoria si deduce anche che, dati due orologi identici, inizialmente in quiete in un riferimento inerziale, se uno, B, prende a muoversi rispetto all’altro, A, percorrendo un cammino chiuso, esso, una volta tornato nel punto di partenza, risulterà in ritardo rispetto a quello rimasto fermo. Se, in particolare, il moto di andata e quello di ritorno avvengono con velocità costante, il p. sorgerebbe quando, considerando il processo dal punto di vista di un osservatore in un sistema di riferimento in cui B è in quiete, e quindi A in movimento, si giungesse a concludere, invocando l’equivalenza tra le due descrizioni, che A deve risultare in ritardo rispetto a B, contrariamente a quanto affermato sopra. Il p. si risolve osservando che, nei periodi in cui B parte, arriva e inverte il moto, il sistema di riferimento solidale con B non è inerziale e quindi non è equivalente a quello iniziale.

Per il p. di d’Alembert ➔ Alembert, Jean-Baptiste Le Rond; per il p. EPR ➔ Einstein, Albert.

Matematica

P. matematico Proposizione contrastante con precedenti risultati o con principi ritenuti incondizionatamente validi, dedotta da una dimostrazione che appare a prima vista rigorosa. È famoso, tra essi, il p. di Zenone (➔ Achille), connesso a un’indebita estensione a insiemi infiniti di principi validi solo per insiemi finiti.

Tipi di paradossi

In logica, il p. è un enunciato contrario all’opinione comune ovvero che si presenta in sé stesso contraddittorio. Allorché si tratta dei cosiddetti p. logici e linguistici, il termine è usato come sinonimo di antinomia. Tra i p. classici si ricordano quelli di Zenone di Elea, le antinomie kantiane (➔ antinomia), quelli dell’infinito (raccolti da B. Bolzano in Paradoxien des Unendlichen, postumo, 1851) ecc.

P. di Epimenide e p. del mentitore Epimenide, cretese, afferma: «Tutti i cretesi sono mentitori». Se questa affermazione fosse vera, allora implicherebbe la propria falsità portando a una contraddizione. L’affermazione di Epimenide è invece falsa: ciò significa che esiste almeno un cretese che abbia detto almeno una volta la verità (non Epimenide in questa occasione). Il p. di Epimenide non è un vero p., ma viene spesso considerato equivalente al p. del mentitore: «Questa frase è falsa». P. di Burali-Forti Ogni insieme bene ordinato ha un suo numero ordinale, ma l’insieme T di tutti i numeri ordinali disposti secondo grandezza è bene ordinato, quindi ha un suo ordinale, massimo tra tutti gli ordinali; indichiamolo con τ. Allora l’insieme bene ordinato secondo grandezza T ⋂ {τ} ha il suo ordinale, che risulta τ+1 e quindi è maggiore di τ; quest’ultimo perciò non è il massimo tra tutti gli ordinali.

P. di Russell Chiamiamo ‘regolari’ gli insiemi che non contengono sé stessi come elementi, ‘irregolari’ quelli che contengono sé stessi come elementi. Sia R l’insieme di tutti e solo gli insiemi regolari. Si domanda se R è regolare o no, cioè se R∈R oppure R∉R. Ma, se R∈R, allora R non è regolare, cioè R∉R. Viceversa, se R∉R, allora R è regolare e quindi R∈R. Cioè, R∈R→R∉R. Il che è assurdo. P. di Richard Si consideri l’insieme D costituito da tutti i numeri reali definibili con un numero finito di parole della lingua italiana. D è numerabile perché è certamente finito il suo sottoinsieme D_k (k = 1, 2, 3, …) costituito da tutti i numeri reali definibili con k parole. D può, allora, essere ordinato in modo naturale disponendo prima il sottoinsieme D₁, poi D₂, poi D₃ ecc., e in ciascuno di questi ordinando a loro volta le varie definizioni lessicograficamente (cioè come in un dizionario). Chiamiamo n-esimo numero di Richard l’n-esimo numero dell’insieme ordinato D. Consideriamo ora il numero reale così definito: «il numero la cui i-esima cifra decimale è 1 se l’i-esima cifra decimale dell’i-esimo numero di Richard è diversa da 1, altrimenti è 2». Questo numero reale è definito con 26 parole, quindi deve appartenere a D, dove occuperà un ben determinato posto, diciamo il p-esimo. Ma, per il modo con cui è stato definito, esso è certamente diverso dal p-esimo numero di Richard nella p-esima cifra. Di qui il paradosso.

P. di Berry È una presentazione semplificata di quello di Richard: in italiano vi è un numero finito di sillabe, perciò finito è anche il numero delle definizioni di numeri naturali formulabili con non più di 50 sillabe. Definiamo numero di Berry «il più piccolo numero naturale non definibile con una frase composta di 50 sillabe al massimo». Ma questa definizione contiene meno di 50 sillabe, dunque, paradossalmente, il numero di Berry è definibile con non più di 50 sillabe.

P. del risvegliatore Secondo il diritto consuetudinario, in un villaggio c’è il risvegliatore che sveglia tutti e solo gli abitanti che non si svegliano da sé. Si domanda chi sveglia il risvegliatore. Non lui stesso, perché lui sveglia solo gli altri, non un altro, perché l’unico che può svegliare altri è lui stesso.

Per il p. di Cantor ➔ Cantor, Georg; per quello di Skolem ➔ Skolem, Thoralf.

Classificazione dei p. e soluzione dei p. linguistici

E.W. Beth ha distinto dai p. gli pseudoparadossi come quello del risvegliatore e simili, in quanto il fatto che una norma di diritto abbia delle conseguenze assurde (non è possibile che esista un tale risvegliatore) non è una contraddizione logica e non interessa perciò la logica ma piuttosto il diritto. I veri p. sono, dunque, caratterizzati dal fatto che essi si riferiscono a concetti logici o matematici: quello di Cantor e di Burali-Forti al concetto di numero cardinale e ordinale, quello di Russell alla nozione di insieme, il p. del mentitore al concetto logico-semantico di verità e falsità; le antinomie di Richard e di Berry ai concetti di definizione e di numerabile; quello di Skolem al concetto di modello e di numerabile. Sono questi i p. dei quali bisogna dare una spiegazione. F.P. Ramsey, nel 1926, riprendendo l’osservazione di G. Peano secondo la quale «l’esempio di Richard non concerne la matematica ma la linguistica», suddivise tutti i p. in due classi, quella delle antinomie logiche e quella della antinomie linguistiche (queste ultime dette pure semantiche o sintattiche). Appartengono alla classe delle antinomie logiche i p. di Burali-Forti, Cantor e Russell, alle antinomie linguistiche tutti gli altri.

Per quanto riguarda le antinomie linguistiche, già Ramsey aveva individuato la loro radice comune nella confusione tra linguaggio e metalinguaggio, confusione superabile mediante la formalizzazione del linguaggio. A. Tarski, nel 1930, dimostrò che non è possibile in generale definire il concetto semantico di verità all’interno della sintassi di una teoria elementare e finalmente risolse così in forma, a quanto pare, definitiva l’antico p. del mentitore. Egli in sostanza fece osservare che non è lecito usare lo stesso enunciato per affermare qualcosa e simultaneamente la verità o la falsità dell’enunciato stesso. Un trattamento simile si può applicare all’antinomia di Berry. Se formalizziamo l’aritmetica in un sistema S con un numero finito di simboli elementari, per es. x, 0, 1, 2, 3, …, 9, sufficienti a esprimere un’infinità di simboli composti: x₀, x₁, x₂, …, allora il numero di Berry resta così definito: «il più piccolo numero del sistema S non definibile con un’espressione di S composta al massimo di 50 simboli elementari». È allora chiaro che il p. non sussiste più. Anche per il p. di Richard si possono fare considerazioni analoghe.

Metodi per evitare i p. logici

Le teorie assiomatiche degli insiemi del tipo di von Neumann, Robinson, Bernays, Gödel sono basate sull’idea esposta da J. von Neumann, secondo cui le antinomie non sorgono dal fatto che si possano costruire aggregati di elementi in corrispondenza di qualsiasi proprietà, bensì dalla pretesa che questi aggregati possano essere sempre considerati, a loro volta, come ‘oggetti matematici’, in altri termini come elementi di un insieme. Esistono infatti aggregati tali che l’ipotesi che tutti i loro elementi costituiscano un insieme conduce a una contraddizione; questi aggregati li chiamiamo inconsistenti o assolutamente infiniti o anche classi (tali sono, per es., la totalità di tutti i concetti, la totalità di tutti gli oggetti matematici). Esistono, al contrario, aggregati tali che tutti i loro elementi costituiscono un insieme, e solo questi aggregati chiameremo appunto insiemi o molteplicità consistenti o infine molteplicità comprimibili. I sistemi assiomatici di R. Robinson (1937), di P. Bernays (1936-1958) e di K. Gödel (1938) possono considerarsi come sviluppi di quello di von Neumann.

Per la teoria semplificata dei tipi, ➔ tipo; per le teorie assiomatiche degli insiemi del tipo di Zermelo, Fraenkel, Skolem, ➔ insieme.

Medicina

Si dice di fenomeno o reazione che si svolge in senso opposto a quello che in linea di massima dovrebbe avvenire: per es., disfagia p., la disfagia che ostacola la deglutizione dei liquidi e non dei solidi.

In psichiatria si parla di p. della comunicazione per indicare la contraddizione che deriva dalla deduzione corretta da premesse coerenti. Sul piano comportamentale, il soggetto si trova nell’impossibilità di operare una scelta, perché le due alternative in contraddizione fra loro sono parti di un unico messaggio.

Psicologia

È detta intenzione p. una tecnica psicoterapeutica, tipica della logoterapia di V.E. Frankl, consistente nell’indurre il paziente a fare ciò di cui prova paura.