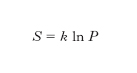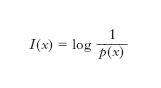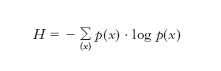entropia
Grandezza che interviene nello studio fisico-chimico delle trasformazioni di un sistema materiale e che dipende unicamente dallo stato del sistema. In termini matematici, si può dire che l’e. è funzione delle sole variabili prescelte a caratterizzare tale stato, la forma della dipendenza essendo diversa a seconda della natura del sistema (gas perfetto, gas reale, liquido ecc.). L’e., come è stato messo in evidenza dalla meccanica statistica, ha un preciso significato microscopico: è la misura del grado di disordine molecolare del sistema ovvero del grado di indeterminazione con il quale si conoscono posizioni e velocità molecolari del sistema stesso. Come misura del grado di disordine o di indeterminazione di un sistema, l’e. è stata utilizzata in campi di applicazione lontani dalla fisica, primo tra tutti la teoria dell’informazione.
E. e termodinamica
La grandezza e. fu introdotta dal fisico tedesco R.J. Clausius nel tentativo di chiarire meglio il significato del secondo principio della termodinamica. La discussione di talune conseguenze del secondo principio mise infatti in luce che se un sistema termodinamico, attraverso una successione di trasformazioni elementari reversibili, passa da uno stato A a uno stato B e da questo ritorna in A, alla generica trasformazione elementare corrispondendo una quantità di calore δQ ceduta o assorbita alla temperatura termodinamica T, si ha
o, ciò che è lo stesso, se il sistema passa, con le stesse modalità, da uno stato A a uno stato B, il valore di
non dipende dalla successione degli stati intermedi ma soltanto dagli stati estremi: ciò equivale appunto a stabilire l’esistenza di una grandezza S, definita in corrispondenza a ogni stato del sistema, la cui variazione tra uno stato A e uno stato B uguaglia l’integrale suddetto. In termini equivalenti si può dire: il rapporto δQ/T viene a presentarsi come il differenziale totale di S,
o ancora: 1/T è fattore integrante di δQ (che non è un differenziale esatto: perciò il segno δ anziché d). La funzione S è l’entropia. Pertanto la variazione dell’e. di un sistema che comunque compia una trasformazione (reversibile o irreversibile) da uno stato A a uno stato B è data da
dove l’integrale va calcolato su una qualsiasi trasformazione reversibile che faccia passare il sistema dallo stato A allo stato B. Come l’energia interna, come il potenziale ecc., l’e. risulta quindi definita a meno di una costante additiva (si possono calcolare le variazioni di S a partire da uno stato di riferimento, ma il valore di S che si attribuisce a tale stato resta arbitrario). Seguendo però l’idea di W.H. Nernst e di M. Planck è da attribuirsi valore nullo all’e. di una qualsiasi sostanza cristallina pura in corrispondenza allo zero assoluto (terzo principio della termodinamica). L’e. nel SI si misura in J/K.
Particolarmente interessanti le conclusioni cui si perviene per un sistema isolato (che cioè non possa cedere o ricevere calore dall’esterno): per qualsiasi trasformazione reversibile l’e. di un tale sistema resta invariata, subisce invece un aumento per ogni trasformazione reale (irreversibile), e all’aumento di e. si accompagna una degradazione dell’energia (trasformazione di lavoro o di altre forme di energia in calore). Ciò significa che se si assimila l’Universo a un sistema isolato, si arriva all’affermazione che l’e. dell’Universo tende ad aumentare e che inoltre in ogni sistema isolato le trasformazioni tendono a prodursi nel verso che si accompagna a un aumento dell’entropia. Lo studio termodinamico di un gas perfetto porta direttamente alla definizione della funzione di stato entropia. Se si considera infatti una trasformazione termodinamica infinitesima reversibile di n moli di un gas perfetto (monoatomico) si ha
essendo k = R/N0 la costante di Boltzmann, R la costante dei gas, N0 il numero di Avogadro, N il numero totale di molecole, Cv=3R/2 il calore molare a volume costante, p e V la pressione e il volume del gas; quindi, a differenza di δQ, δQ/T è per un gas perfetto (e il risultato, come si è visto, è estendibile a un qualsiasi sistema termodinamico solo sulla base del 2° principio della termodinamica) il differenziale esatto della funzione di stato e. (definita a meno di una costante arbitraria)
E. e disordine
Sulla base dell’espressione dell’e. di un gas perfetto si può precisare il significato microscopico dell’e. come misura del disordine molecolare. La probabilità che una molecola di un gas perfetto (in equilibrio termodinamico e in assenza di campi di forza) abbia la componente α-sima della velocità compresa tra vx e vx+dvx è data da
dove m è la massa di una molecola. Le funzioni di distribuzione f (vα) delle componenti della velocità sono cioè gaussiane centrate intorno allo zero con varianza σ2=kT/m: con probabilità praticamente uguale a 1 la velocità di una molecola è compresa nel ‘volume’ dello spazio delle velocità (2 ∙ 3σ)3=[63 ∙ (k/m)3/2] ∙ T 3/2
Pertanto la grandezza VT 3/2 che compare nell’espressione [1] dell’e. di un gas perfetto è proporzionale al prodotto del volume dello spazio ordinario occupato dalle molecole (che all’equilibrio coincide con il volume del recipiente nel quale sono racchiuse) per il ‘volume’ dello spazio delle velocità occupato dalle velocità delle molecole stesse. Poiché intuitivamente il disordine delle molecole di un gas perfetto è tanto maggiore quanto maggiore è il volume da esse occupato (all’aumentare di questo volume le molecole del gas sono sempre più sparse), ed è anche tanto maggiore quanto più diverse sono le loro rispettive velocità (cioè quanto maggiore è il volume dello spazio delle velocità che esse occupano), il prodotto V · T 3/2 è proprio una misura del disordine molecolare e lo è di conseguenza anche l’entropia. Questo risultato può essere ottenuto in modo rigoroso con i metodi della meccanica statistica (e può essere esteso a qualsiasi sistema). Si dimostra infatti che, a meno di una costante additiva, l’e. di un gas perfetto in equilibrio termodinamico è esprimibile come
dove dω = dx dy dz dvx dvy dvz è l’elemen;to dell’iperspazio delle coordinate e delle componenti della velocità (che coincide, nel caso in cui tutte le molecole abbiano, come qui e nel seguito supponiamo, massa uguale, con lo spazio delle fasi), l’integrale è esteso a tutto lo spazio delle fasi, e f è la funzione di distribuzione del gas definita in modo tale che f dω sia la probabilità dp che una molecola si trovi nel volumetto dx dy dz (abbia cioè coordinate comprese tra x e x+dx, y e y+dy, z e z+dz) con componenti della velocità comprese tra vx e vx+dvx, vy e vy+dvy, vz e vz+dvz. Questa espressione dell’e. di un sistema in equilibrio termodinamico può essere estesa come definizione dell’e. anche agli stati di non equilibrio. L’e., che per la [2] risulta proporzionale al valore medio del logaritmo della funzione di distribuzione, è tanto maggiore quanto più è estesa la regione di spazio delle fasi nella quale la funzione di distribuzione è diversa da zero (regione entro la quale sono ‘confinate’ le molecole), cioè quanto maggiore è il disordine molecolare. Poiché il ‘volume’ di spazio delle fasi entro il quale sono confinate le molecole del gas è una misura del grado di indeterminazione con il quale conosciamo la posizione e la velocità delle molecole, anche l’e. è una misura di questa indeterminazione, cioè della mancanza di informazione sullo stato microscopico del sistema.
E. e probabilità termodinamica
L. Boltzmann per primo stabilì la connessione tra e. e stati microscopici di un sistema definendo la probabilità termodinamica P di uno stato macroscopico come il numero di modi nel quale tale stato può essere realizzato con configurazioni microscopiche diverse (per posizione e velocità delle singole molecole) e postulando poi l’esistenza di una relazione funzionale tra l’e. S e la probabilità termodinamica P. Poiché se si considerano due sistemi A e B come un unico sistema l’e. complessiva è uguale alla somma delle e., mentre la probabilità complessiva è uguale al prodotto delle probabilità dei sistemi componen;ti, la relazione funzionale tra e. e probabilità termodinamica deve essere del tipo S ∝ lnP. A questo risultato si può giungere nel caso di un gas perfetto senza postulare la predetta dipendenza funzionale tra S e P, sulla base di semplici considerazioni. In questo caso infatti, come si è visto precedentemente, una molecola del gas è confinata in un ‘volume’ dello spazio delle fasi W ∝ VT 3/2. Poiché lo stato di una molecola è rappresentato da un punto nello spazio delle fasi, cioè dalla 6-pla di numeri che esprimono le coordinate spaziali e le componenti della velocità della molecola (x, y, z, vx, vy, vz), gli stati contenuti nel ‘volume’ W sono ∞6. Si possono però ritenere praticamente ‘identici’ stati molto vicini tra loro, cioè compresi in un volumetto dello spazio delle fasi w molto piccolo. Questo discorso, che nell’ambito della fisica classica è piuttosto qualitativo, assume completo rigore nell’ambito della meccanica quantistica secondo la quale sono fisicamente indistinguibili stati contenuti nel volumetto dello spazio delle fasi w = h3/m3, essendo h la costante di Planck; questa è una conseguenza immediata del principio di indeterminazione secondo il quale la misura simultanea di una coordinata spaziale di una particella e della omologa componente della velocità è affetta dalla indeterminazione Δx · Δvx ≳ h /m: non ha quindi senso fisico alcuno distinguere stati all’interno del volumetto dello spazio delle fasi Δx Δvx Δy Δvy Δz Δvz = h3/m3. Il numero di stati che può assumere una molecola di un gas perfetto alla temperatura T, racchiuso in un volume V, è quindi
Se le molecole che costituiscono il gas sono N, il numero di stati microscopici che possono assumere le N molecole costituenti il dato stato macroscopico è
Confrontando la [3] con la [1] si ottiene, a meno di una costante additiva,
che è proprio la relazione di Boltzmann, cioè l’e. è proporzionale al logaritmo della probabilità termodinamica. Poiché la probabilità termodinamica è tanto maggiore quanto maggiore è il disordine di un sistema, in quanto all’aumentare del disordine aumenta il numero di stati microscopici che portano al dato stato macroscopico, anche dalla relazione di Boltzmann risulta che l’e. è una misura del disordine molecolare.
E., probabilità e informazione
L’e. nella teoria dell’informazione è una misura del grado di complessità di un messaggio emesso da una sorgente; essa fornisce infatti, come dimostrato nel primo teorema di Shannon, il numero medio minimo di simboli necessari a una codifica del messaggio stesso. Per definire la quantità di informazione contenuta nei simboli emessi da una sorgente discreta, considerando solo l’aspetto sintattico del messaggio e non quello semantico o pragmatico, si richiede in genere che l’informazione ottenuta dal riscontro di un evento sia una quantità positiva o al più nulla, che sia additiva per eventi indipendenti e infine che sia una funzione continua della probabilità dell’evento (➔ informazione). Nel caso di una sorgente senza memoria, ossia di una sorgente per la quale la probabilità p(x) di emettere il simbolo x non dipende da quelli precedentemente emessi, si misura l’incertezza di x definendo la quantità di informazione in esso contenuta come:
e l’e. della sorgente, H, o e. per simbolo, è data dal valore medio dell’incertezza:
dove la somma va intesa sull’insieme {x} di tutti i valori che possono assumere i simboli e log è il logaritmo in base due se l’e. è espressa in bit, in base dieci se espressa in hartley, in base e se espressa in nat. Per una sequenza illimitata di simboli, ognuno dei quali con M possibili valori, emessi da una sorgente discreta (per es. una sorgente numerica decimale con M =10 o una sorgente alfabetica con M =27), H raggiunge il suo valore massimo, pari a log M, se i simboli sono equiprobabili, ovvero quando p(x)=1/M per ogni x.
Molto adoperato nello studio dei cicli delle macchine termiche è il diagramma entropico (o di Carnot), avente in ascissa l’e., in ordinata la temperatura termodinamica.

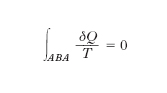
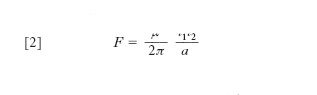
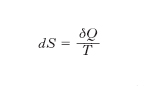
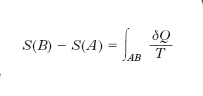
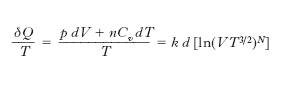
![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b1/FORMULE_entropia_06.jpg)
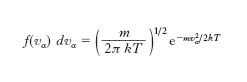
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/34/FORMULE_entropia_08.jpg)
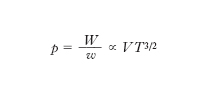
![[3]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/5b/FORMULE_entropia_10.jpg)