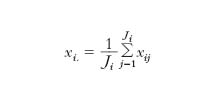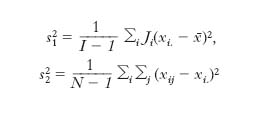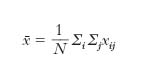varianza

varianza fisica In termodinamica, la v. (o grado di libertà), è il numero dei parametri caratteristici di un sistema che si possono far variare senza cambiare il numero e la natura delle fasi presenti (➔ equilibrio). matematica In statistica, data la successione di valori numerici esprimenti un dato carattere quantitativo in una popolazione, la v. è la media aritmetica dei quadrati degli scarti dei valori dalla loro media aritmetica; la sua radice quadrata, presa con segno positivo, è lo scarto quadratico medio. Se i dati sono campionari, si usa spesso calcolare la v. corretta, che è il prodotto della v. per il fattore N/(N−1), dove N è il numero delle unità che compongono il campione; risulta che la v. corretta del campione è una stima corretta della v. della popolazione se l’estrazione del campione è bernoulliana, e una stima corretta della v. corretta della popolazione se l’estrazione è senza ripetizione. Analisi della v. Tecnica statistica, ideata da R.A. Fisher, per analizzare osservazioni campionarie di fenomeni dipendenti da uno o più fattori, al fine di decidere quali fattori sono rilevanti e di stimarne gli effetti. Nel caso di un solo fattore che si presenti in I modalità o ‘livelli’ (per fissare le idee, si può trattare, per es., di I varietà di grano, coltivate in condizioni ambientali identiche), il punto di partenza è costituito da un modello del tipo: xij=βi+eij, con i=1, ..., I; j=1, ..., Ji, dove xij è la j-esima osservazione campionaria associata al livello i-esimo del fattore considerato (nel nostro esempio, le x potrebbero rappresentare raccolti su parcelle di dimensioni uguali), i parametri ignoti βi misurano l’effetto prodotto dai diversi livelli del fattore stesso (nel nostro esempio, le diverse varietà di grano) e le eij rappresentano la componente casuale. Si assume che le eij siano variabili normali indipendenti con media nulla e varianza incognita σ2. Le stime (corrette ed efficienti) delle βi sono le distribuzioni marginali:

Le quantità

dove N=Σ_iJ_i è il numero totale delle osservazioni e

è la media aritmetica generale, sono determinazioni di variabili casuali indipendenti. Per verificare l’ipotesi che tutte le β_i siano uguali (cioè, nel nostro esempio, che le diverse varietà di grano diano, a meno di variazioni casuali, lo stesso rendimento) ci si serve del rapporto s₁²/s₂² il quale, se l’ipotesi è vera, si distribuisce come la variabile F (di Fisher-Snedecor) centrale con I−1 e N−I gradi di libertà. Pertanto, fissato un livello di significatività α, l’ipotesi viene accettata o respinta secondo che s₁²/s₂²≤0 oppure >F_{α; I−1}, _N−I, dove F_{α; I−1}, _N−I è il punto nel quale la funzione di ripartizione della variabile in questione assume il valore 1−α. Ciò è giustificato dal fatto che in tal modo la probabilità di respingere l’ipotesi è maggiore quando essa è falsa che quando è vera, e pertanto il test gode della proprietà di correttezza. La variabile s²₂ è una stima corretta di σ², quali che siano le β, la variabile s²₁ lo è soltanto se le β_i sono uguali. Vari procedimenti possono essere usati per verificare altre ipotesi lineari riguardanti i parametri β.