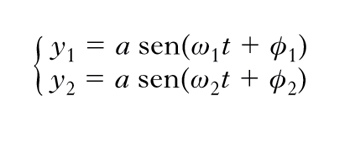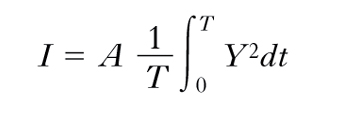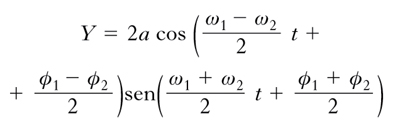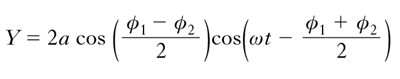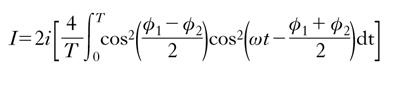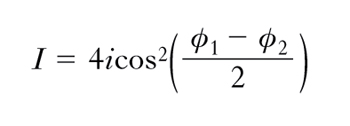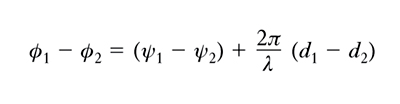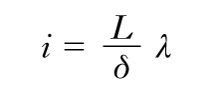interferenza

Biologia

In genetica, il fenomeno per cui in prossimità di un crossing-over non si verificano altri scambi. È questa l’interferenza positiva. Se uno scambio genetico fa aumentare la probabilità che nella regione interessata se ne verifichino altri, si ha l’i. negativa.

Fisica

Con riferimento a fenomeni vibratori e ondulatori, per i. s’intende il sovrapporsi di fenomeni del genere e anche, più concretamente, gli effetti che da tale sovrapposizione derivano. Tali effetti consistono in un reciproco rafforzamento di quelli dovuti ai singoli fenomeni interferenti, e si parla allora di i. costruttiva; altre volte, invece, si ha un’eliminazione (o anche soltanto un’attenuazione) reciproca dei singoli effetti e si parla allora di i. distruttiva.

Sovrapposizione di grandezze vibratorie

Per semplicità, verrà presa in esame la sovrapposizione di due sole grandezze vibratorie, indicate con y₁, y₂: nel caso di onde sonore, potrebbero rappresentare gli spostamenti delle molecole del mezzo in cui le onde si propagano; nel caso di onde elettromagnetiche, e luminose in particolare, potrebbero rappresentare le intensità dei campi elettrici, e così via. Si osservi che per il verificarsi di i. tra le due grandezze considerate occorre che sia soddisfatta una prima, ovvia, condizione: precisamente, occorre che esse vengano ad agire in una stessa regione di spazio. Si consideri dunque un punto P in cui siano contemporaneamente presenti le due vibrazioni, e che le direzioni di vibrazione delle due grandezze in P coincidano; se infatti le direzioni di vibrazione non coincidono, non si ha l’i. propriamente detta ma, semplicemente, una composizione di moti vibratori svolgentisi in direzioni diverse (➔ moto). Le due vibrazioni, che per semplicità vengono supposte armoniche e di uguale ampiezza, saranno rappresentate in P da equazioni del tipo:

[1]  formula

Come d’uso, con a si è indicata l’ampiezza, con ω la pulsazione, con ϕ la fase iniziale, con t il tempo. La vibrazione Y risultante in P è, istante per istante,

[2] Y = y1 + y2.

L’intensità energetica, I, della vibrazione risultante in P è proporzionale al valore quadratico medio dell’ampiezza istantanea Y; si ha, cioè,

[3] formula

essendo A la costante di proporzionalità, dipendente dalla natura delle vibrazioni e del mezzo, nonché dal sistema di unità di misura adottato, e T un comune multiplo dei periodi delle due vibrazioni. Come si riconosce ricorrendo alle formule di prostaferesi, le [1], [2] danno in generale

La vibrazione risultante ha dunque una pulsazione pari a (ω₁+ω₂)/2 e un’ampiezza che varia nel tempo sinusoidalmente, con pulsazione ∣ω₁−ω₂∣/2. Applicando poi la [3], si riconosce che l’intensità di essa è semplicemente la somma delle intensità delle due vibrazioni. Se dunque, come sin qui implicitamente ammesso, le due vibrazioni hanno pulsazione diversa (e quindi frequenza, periodo, lunghezza d’onda diversi), l’i. consiste semplicemente nella somma degli effetti; al più, si ha battimento tra le vibrazioni. Ben diversamente vanno invece le cose se le pulsazioni sono uguali. Indicando allora con ω il comune valore di ω₁ e ω₂, si ha infatti:

indicando con i il comune valore dell’intensità delle due onde (i=a²/2), per l’intensità complessiva in P si ha, dalla [3]:

Se la differenza tra le fasi iniziali in P, (ϕ₁−ϕ₂), varia casualmente nel tempo, cioè se le due vibrazioni sono ‘incoerenti’, il termine tra parentesi quadre è uguale a 1: l’i., ancora una volta, si riduce al banale sommarsi delle singole intensità. Se invece (ϕ₁−ϕ₂) è costante nel tempo, cioè se le due vibrazioni sono ‘coerenti’, si ha:

Ogniqualvolta è cos² [(ϕ₁−ϕ₂)/2]=1, cioè

[4] ϕ₁ − ϕ₂ = 2kπ,

con k nullo o intero, le due vibrazioni sono in accordo di fase ed è I=4i: si ha i. costruttiva, l’intensità risultando il doppio della somma delle intensità singole. Ogniqualvolta è, invece,

cos² [(ϕ₁ − ϕ₂)/2] = 0,

cioè

[5] ϕ₁ − ϕ₂ = (2k + 1)π,

con k nullo o intero, le due vibrazioni sono in opposizione di fase ed è I=0: si ha i. distruttiva, l’intensità essendo nulla.

Condizioni fisiche essenziali per il verificarsi dell’i. propriamente detta, oltre quelle geometriche dianzi ricordate, sono dunque che le due vibrazioni abbiano la stessa pulsazione e siano coerenti. Come le [4] e [5] mostrano per due casi particolari, le modalità con cui l’i. si presenta dipendono dalla differenza tra le fasi iniziali delle due vibrazioni (coincidente, a causa dell’uguaglianza delle pulsazioni, con la differenza tra le fasi istantanee) nel punto P. Ognuna di tali fasi iniziali è la somma di due termini, il primo dei quali è la fase iniziale della vibrazione nella sorgente, ψ, mentre il secondo è la differenza di fase tra le vibrazioni nella sorgente e quelle in P, dovuta al fatto che la perturbazione vibratoria impiega un certo tempo per giungere in P dalla sorgente; precisamente, per la differenza complessiva di fase in P si ha:

[6] formula

fig. 1

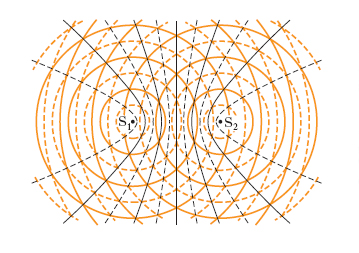
λ essendo la lunghezza d’onda, che nel caso in esame è la stessa per le due vibrazioni, e d₁, d₂ essendo le distanze di P dall’una e dall’altra sorgente. Si osservi che la coerenza delle vibrazioni in P implica necessariamente la ‘coerenza delle sorgenti’. Ammettendo dunque che le sorgenti siano coerenti, i due parametri che governano insieme il verificarsi in P dell’i., in particolare di quella distruttiva, sono la ‘differenza di fase tra le sorgenti’, (ψ₁−ψ₂), e la ‘differenza di cammino’, (d₁−d₂), tra P e le sorgenti medesime. Se in particolare, come molto spesso avviene, le sorgenti sono in immutabile accordo di fase, cioè se è comunque ψ₁−ψ₂=0, parametro essenziale resta la sola differenza di cammino. Come si riconosce dalle [4], [5], [6], si ha in P i. costruttiva se è d₁−d₂=2kλ/2, cioè se la differenza di cammino è uguale a un numero pari di mezze lunghezze d’onda; si ha invece i. distruttiva se è d₁−d₂=(2k+1)λ/2, cioè se la differenza di cammino è uguale a un numero dispari di mezze lunghezze d’onda. Com’è noto, il luogo dei punti dello spazio le cui distanze da due punti dati differiscono di una data quantità è una superficie iperboloidica avente per fuochi i due punti in questione. Così, se si considerano due sorgenti puntiformi, coerenti e in fase, le onde sferiche emesse dalle due interferiscono nello spazio circostante e le superfici luogo dei punti in cui l’i. ha uno stesso carattere, per es. è distruttiva, sono appunto iperboloidiche, con fuochi nelle sorgenti medesime. La fig. 1 mostra le iperboli intersezioni di tali superfici con un piano contenente le due sorgenti coerenti, S₁, S₂, puntiformi (e quindi emettenti onde sferiche); sono a tratto pieno le curve luogo dei punti in cui si ha i. costruttiva, e tratteggiate quelle in cui si ha i. distruttiva. In virtù dell’i., l’intensità energetica dei due sistemi di onde, che dovrebbe distribuirsi uniformemente tutt’intorno alle sorgenti, risulta ‘addensata’ intorno alle superfici a cui corrisponde una differenza di cammino dalle sorgenti uguale a multipli pari di λ/2, ‘rarefatta’ intorno alle superfici cui corrisponde una differenza di cammino uguale a multipli dispari di λ/2. Questa singolare ridistribuzione di energia ondulatoria, in cui sostanzialmente consiste il fenomeno dell’i., si ha anche se si prendono in esame situazioni più complesse di quella, relativamente semplice, considerata sinora.

Sul fatto che la distribuzione spaziale dell’intensità della radiazione risultante dall’i. viene a dipendere dalla lunghezza d’onda sono basate importanti applicazioni dei fenomeni interferenziali, quali la misurazione accurata di lunghezza (➔ interferometria), la realizzazione di filtri, appunto detti interferenziali (➔ filtro), la misurazione di lunghezze d’onda e la produzione di spettri.

I. della luce

fig. 2

fig. 3

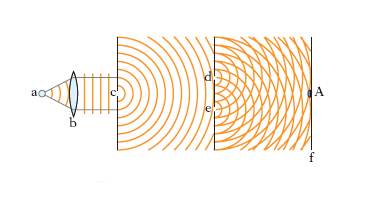
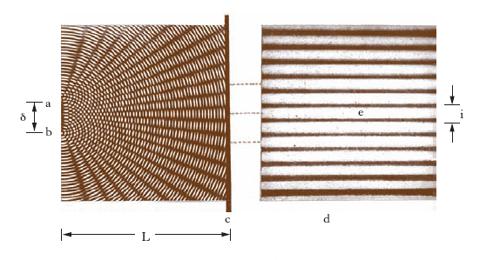
Nel complesso di tutti i vari possibili fenomeni interferenziali, quelli relativi all’i. della luce hanno particolare interesse anche dal punto di vista storico; essi, tra l’altro, hanno costituito il più valido argomento a favore delle teorie ondulatorie sulla natura della luce nella secolare disputa fra queste e le cosiddette teorie corpuscolari. L’i. della luce si rende generalmente manifesta con la formazione di caratteristiche figure luminose dette figure d’interferenza. La coerenza tra le sorgenti, condizione essenziale, secondo quanto detto prima, al verificarsi del fenomeno, non può ottenersi nel caso di due sorgenti luminose distinte, anche se di identiche caratteristiche fisiche, cioè anche se emettenti luce di identica composizione spettrale e di uguale intensità. Il motivo di ciò sta nel fatto che una sorgente luminosa non emette un’onda, ma un gran numero di onde ‘elementari’ che hanno tutte la stessa pulsazione se la sorgente è monocromatica ma la cui fase iniziale (come anche la polarizzazione) varia dall’una all’altra, corrispondentemente alla distribuzione casuale nel tempo degli atti elementari di emissione (il ritorno di elettroni eccitati allo stato fondamentale) dai quali le singole onde si originano. Il grado di coerenza temporale (➔ coerenza) di una sorgente siffatta – e il discorso vale per tutte le sorgenti di onde elettromagnetiche, eccezion fatta per le antenne radiotrasmittenti e i laser – è nullo su tempi relativamente lunghi, quali sono quelli dell’osservazione ordinaria. Si immagini invece di far interferire tra loro le onde provenienti da una medesima sorgente, per es. isolando mediante fenditure due porzioni diverse di superfici d’onda o facendo percorrere alle onde cammini diversi, mediante dispositivi riflettenti o rifrangenti. In questo caso nella [6] viene meno il termine (ψ₁−ψ₂) in quanto l’i. ha luogo tra raggi di ogni onda elementare, i quali sono polarizzati nello stesso piano e nella sorgente sono ovviamente in fase tra loro; il carattere dell’i. viene allora a dipendere soltanto dalla differenza di cammino: così l’i. ha, se la differenza di cammino è sufficientemente piccola, in un dato punto lo stesso carattere per tutte le onde elementari ed è allora osservabile. Le cose, in definitiva, vanno come se alla sorgente effettiva venisse sostituita una coppia di sorgenti fittizie, coerenti tra loro. Questo è il principio comune a tutti i dispositivi per produrre l’i. della luce, che differiscono tra loro unicamente per l’artificio messo in opera al fine di creare le anzidette sorgenti fittizie. Nella fig. 2 è illustrata schematicamente la disposizione adottata da T. Young (1802). I raggi emessi dalla sorgente puntiforme monocromatica a, resi paralleli dalla lente b, vengono inviati su uno schermo provvisto di una fenditura c; i raggi partenti da quest’ultima, che funge da sorgente lineare, investono un secondo schermo provvisto di due sottili fenditure d ed e, parallele e vicine. Le due fenditure costituiscono, in virtù del principio di Huygens, due sorgenti luminose coerenti. Interponendo sul cammino dei raggi provenienti da esse uno schermo opaco f, come in fig. 2, varia su questo da punto a punto la differenza dei cammini rispetto alle due fenditure, e quindi l’intensità luminosa dell’onda risultante dall’i.: la figura di i. è in tal caso costituita da una serie di strisce parallele (frange di i.) alternativamente chiare e oscure. Se, come nella fig. 2, le due fenditure, d, e, sono a uguale distanza dalla fenditura sorgente, c, nei punti A dello schermo f equidistanti dalle due fenditure la differenza di cammino è nulla; si ha in questo punto i. costruttiva, con la formazione di una frangia brillante, la frangia centrale. Se lo schermo con le fenditure è parallelo a quello su cui si osservano le frange, queste si dispongono simmetricamente intorno alla frangia centrale e (fig. 3). Indicando con L la distanza tra gli schermi, con δ la distanza tra le fenditure e con i l’interfrangia, vale a dire la distanza tra due frange consecutive, per es., oscure (fig. 3), in queste condizioni tra tali grandezze passa, come si dimostra, la relazione:

[7]  formula

essendo λ la lunghezza d’onda della luce. Si comprende di qui la possibilità di utilizzare il fenomeno dell’i. per misurare lunghezze (note che siano λ, i, δ, si può ricavare la distanza L tra gli schermi) o lunghezze d’onda (basta allora misurare L, δ, i); misurazioni del genere si effettuano mediante apparecchi, detti interferometri (➔ interferometria), che adottano la disposizione ora descritta o una tra le tante altre equivalenti.

Particolarmente interessanti, anche per le applicazioni che se ne fanno in varie discipline, sono i fenomeni d’i. fra i raggi, provenienti da una stessa sorgente, che si riflettono e si rifrangono in una sottile lamina trasparente, per es., una sottile lamina di vetro, la lamina d’aria compressa fra due lastre di vetro ecc.

Interferenza di particelle

In conformità con i principi della meccanica quantistica, anche le radiazioni particellari, vale a dire fasci di elettroni, di neutroni ecc., danno luogo a fenomeni di interferenza. Che fenomeni del genere avvengano è dimostrato dal successo dei vari metodi sperimentali per studi di strutturistica basati sulla diffrazione di particelle, e in particolare di elettroni e di neutroni (➔ diffrazione).

Linguistica

In semantica, una delle cause delle trasformazioni di significato di una parola, consistente nel sovrapporsi di un secondo significato a un primo in connessione con etimologie popolari o semidotte: per es., l’uso di inedia con il significato di «tedio, noia», dovuto a una sovrapposizione di inerzia. Più generalmente, in linguistica, l’influenza che in singoli casi e come fenomeno individuale una lingua può esercitare su un’altra lingua in contatto, soprattutto in soggetti bilingui, portando a modificazioni fonetiche, morfologiche, sintattiche o lessicali: per es., un italiano può incorrere nell’erroneo calco ma machine per ma voiture.