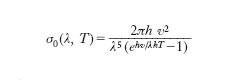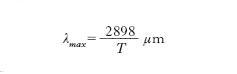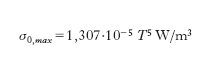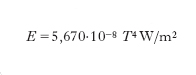còrpo néro

còrpo néro In fisica, corpo dotato della proprietà di assorbire tutte le radiazioni elettromagnetiche che lo investono, caratterizzato pertanto da un fattore di assorbimento (o potere assorbente) pari all'unità per radiazioni elettromagnetiche di qualsivoglia lunghezza d'onda (principio di Kirchhoff).

Nessun corpo materiale è ‘nero’ per tutte le radiazioni, pur potendo taluni esserlo per le radiazioni di alcune zone dello spettro (per es., il nerofumo per le radiazioni dello spettro visibile). È possibile tuttavia realizzare un dispositivo che sostanzialmente si comporta come un corpo nero, praticando un forellino in un corpo cavo, di forma qualunque, a pareti opache alle radiazioni e internamente annerite con nerofumo o nero di platino: le radiazioni che dal foro penetrano nell’interno finiscono, dopo una serie di successive riflessioni, con l’essere pressoché totalmente assorbite dalle pareti (è questo il motivo per cui l’apertura di accesso di una grotta, una stanza ecc., che non siano internamente illuminate, appare a chi guardi dall’esterno oscura).

La denominazione di corpo nero e il primo studio delle sue proprietà si devono a G.R. Kirchhoff, nel corso delle sue classiche ricerche sull’emissione termica. Studiando l’equilibrio termodinamico che deve stabilirsi, per ogni elemento di superficie, tra energia raggiante assorbita ed emessa in un corpo in equilibrio termico con l’ambiente circostante, Kirchhoff pervenne ad affermare, secondo la legge che porta il suo nome, che per un corpo mantenuto a una temperatura costante T, il rapporto tra la brillanza specifica (o potere emissivo per unità di superficie e per intervallo unitario di lunghezza d’onda) σ (λ, T) e il fattore di assorbimento specifico (cioè per unità di superficie e per intervallo unitario di lunghezza d’onda) α (λ, T) è funzione soltanto della lunghezza d’onda λ e della temperatura termodinamica T (e quindi indipendente dalla natura del corpo) ed è uguale alla brillanza specifica σ₀ (λ, T) del corpo nero alla temperatura T (per il quale α = 1); il che equivale a dire che un corpo assorbe, a una data temperatura, le radiazioni che esso, a quella stessa temperatura, è in grado di emettere (circostanza, quest’ultima, messa bene in evidenza dal fenomeno dell’inversione). Com’è chiaro, la conoscenza della funzione universale σ₀ (λ, T) permette, quando sia noto, per un dato corpo, α (λ, T) in un certo campo di lunghezze d’onda e di temperature, di ricavare σ (λ, T) o viceversa; vale a dire permette di determinare le proprietà emettenti di un corpo a partire da quelle assorbenti o viceversa: in ciò sta la grande importanza dello studio dell’emissione del corpo nero. Per la legge di Planck, la brillanza specifica del corpo nero è:

,

fig

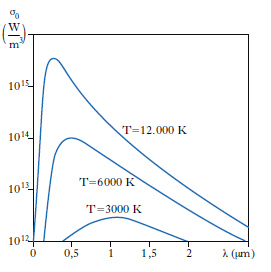
dove h è la costante di Planck, v la velocità di propagazione delle onde elettromagnetiche nel mezzo in cui il corpo nero è immerso, e la base dei logaritmi naturali, k la costante di Boltzmann e T la temperatura termodinamica. In base alla [1] possono essere costruite le curve che danno l’andamento di σ₀ in funzione di λ per T costante; in fig. sono riportate le curve relative al campo di lunghezze d’onda sino a circa 2,5 μm e alle temperature di 3000 K (all’incirca la temperatura del filamento di una lampada elettrica a incandescenza), 6000 K (all’incirca quella della fotosfera solare), 12.000 K (all’incirca quella degli elettroni in una lampada elettrica a scarica). Tali curve sono in ottimo accordo con i risultati dell’esperienza (le prime determinazioni al riguardo sono dovute a O. Lummer e A. Pringsheim). Come appare dalla figura, la lunghezza d’onda λmax corrispondente al massimo valore, σ_0,max di σ₀ (λ, T) è tanto minore quanto maggiore è T; tale fatto, noto come legge di Wien dello spostamento (del massimo di emissione), o prima legge di Wien, è espresso dalla relazione:

Quanto al valore massimo di σ₀, si ha:

,

relazione nota come legge di Wien del massimo, o seconda legge di Wien. Va ricordato infine che, a norma della legge di Stefan-Boltzmann, la radianza integrale E, vale a dire l’energia irraggiata, nel semispazio antistante, dal corpo nero nell’intero campo delle radiazioni elettromagnetiche per unità di tempo e di superficie, è proporzionale alla quarta potenza della temperatura:

In altri termini, l’irraggiamento del corpo nero cresce molto rapidamente al crescere della temperatura.

Lo studio della radiazione del corpo nero ha svolto, all’inizio del 20° sec., un ruolo fondamentale per la nascita della fisica dei quanti. Per ottenere la legge di Planck è infatti indispensabile fare l’ipotesi che l’energia degli atomi che emettono e assorbono la radiazione sia quantizzata; questa, che M. Planck (1900) riteneva essere una semplice ipotesi matematica introdotta ad hoc per spiegare il comportamento sperimentale del corpo nero, si è poi rivelata una proprietà fondamentale dei sistemi atomici. Inoltre, A. Einstein (1905) ha mostrato che la radiazione del corpo nero corrispondente alle piccole lunghezze d’onda (λ ≪ hv/kT) si comporta come un insieme di enti mutuamente indipendenti, ciascuno dotato dell’energia hν, da lui denominati ‘quanti di luce’; questa ipotesi costituisce il punto di partenza della meccanica ondulatoria.