computazionale

Attributo di disciplina che utilizza nell’indagine teorica l’elaboratore elettronico come sistematico strumento di lavoro, per es. la meccanica c., la linguistica c.; si dice c. anche il procedimento che utilizza l’elaboratore elettronico e il risultato ottenuto mediante il suo impiego.

Di particolare importanza è stato l’affermarsi, nella seconda metà del 20° sec., delle metodologie c. in fisica e chimica e nelle scienze applicate, come modalità complementare (e a supporto di) all’indagine teorica e, in certa misura, alla sperimentazione. Nelle discipline scientifiche, l’approccio c. avviene tramite una successione di fasi: individuazione del problema e sua modellazione, definizione di un algoritmo per la soluzione del modello, stesura di un programma di calcolo (in gergo ‘codice’), esecuzione del codice (e quindi ‘simulazione’ del problema), analisi dei risultati. Sebbene ciascuna di queste fasi sia riconducibile a una specifica disciplina (individuazione del problema, modellazione e analisi dei risultati alla specifica scienza – fisica, chimica ecc. –, sviluppo dell’algoritmo alla matematica applicata, stesura del codice alla programmazione), queste fasi sono fra loro strettamente interdipendenti. Tale interdipendenza è connessa alla necessità di giungere a un ragionevole compromesso fra l’accuratezza dello studio e la sua complessità (in termini sia di modello, sia di potenza e tempo di calcolo richiesti). Da questa interdipendenza nasce la specificità delle singole discipline computazionali.

Matematica

I metodi c. si utilizzano per risolvere mediante elaboratori elettronici i problemi complessi che all’interno delle varie scienze fondamentali o applicate sono formulabili tramite il linguaggio della matematica. Molto spesso, infatti, tali problemi non sono risolubili per via analitica in quanto la loro soluzione non ammette una rappresentazione in forma esplicita, come nel caso di problemi che si traducono in equazioni non lineari (algebriche, differenziali o integrali) di cui non siano note le formule risolutive. In altri casi la forma esplicita, pur nota, non è praticamente utilizzabile per determinare valori quantitativi della soluzione stessa, perché essa richiederebbe una quantità di operazioni proibitiva anche per i più moderni elaboratori elettronici.

Risoluzione di un problema applicativo

La risoluzione di un problema applicativo comporta diverse fasi: a) l’interpretazione del problema; b) la sua modellizzazione attraverso equazioni che costituiscono il modello matematico; c) l’individuazione di metodi della matematica numerica che siano idonei ad approssimare tale modello matematico; d) l’implementazione di tali metodi numerici di approssimazione su un elaboratore, cioè la loro traduzione e attuazione in un programma di calcolo. La fase c è indispensabile ogniqualvolta il modello matematico abbia una dimensione infinita e richieda pertanto di essere sostituito da una successione di problemi numerici ciascuno di dimensione finita (discretizzazione). Questi metodi comprendono ed esauriscono le fasi c e d; la loro scelta non può comunque prescindere da una conoscenza adeguata delle proprietà qualitative della soluzione del modello matematico e da una buona percezione della fenomenologia del problema originario. È pertanto giustificata la denominazione di modelli c., usata in alternativa a quella di metodi, e di modellistica c. per il settore di ricerca interdisciplinare, alla confluenza della matematica, dell’informatica e delle varie scienze, che studia tali modelli. L’evoluzione di quest’ultima è stata particolarmente rapida grazie al notevole sviluppo degli elaboratori e degli algoritmi, nonché a una maggiore consapevolezza del ruolo che essa può rivestire nella risoluzione di complessi problemi di interesse scientifico, industriale, economico, sociale ecc.

fig. 1

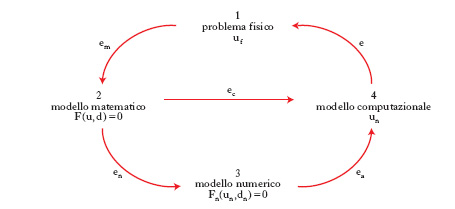
Le varie fasi della risoluzione di un problema applicativo possono essere riassunte in forma schematica mediante il diagramma riportato in fig. 1. Si indica con u_f la soluzione del problema originario, detto per brevità problema fisico, che può provenire da qualsiasi scienza fondamentale o applicata, quale la fisica, la chimica, le scienze biologiche e mediche, l’ingegneria, l’economia ecc. Il modello matematico che descrive il problema fisico è posto nella forma F(u,d)=0, dove d descrive l’insieme dei dati, u la soluzione, F la relazione funzionale che lega fra loro dati e soluzione. Vari e diversificati sono i problemi matematici che, in astratto, possono essere formulati in questo modo. Si consideri, per es., l’integrazione definita di una funzione: si tratta di trovare un numero u tale che l’integrale definito su una regione R della funzione f ivi integrabile sia uguale a esso (in questo caso i dati sono d={R, f} e la soluzione è costituita da u). Molto spesso la funzione f non è integrabile in modo elementare; inoltre il problema ha dimensione ‘infinita’ essendo l’integrale un’operazione esprimibile attraverso il passaggio al limite. Un altro esempio è fornito dal problema di trovare u tale che P(u)=0, dove P è un polinomio di grado r; in questo caso i dati sono costituiti dagli r+1 coefficienti del polinomio e la soluzione dalle r radici complesse del polinomio P di grado r, la cui esistenza è assicurata dal teorema fondamentale dell’algebra. Pur essendo questo problema posto in dimensione finita, le sue soluzioni (le radici di P) non sono note in forma esplicita quando r>4 e servono dunque metodi numerici che consentano di trovare valori approssimati di u. Un altro problema è quello dell’integrazione di equazioni (o sistemi di equazioni) differenziali ordinarie. Si può infine citare l’insieme dei problemi differenziali, stazionari o evolutivi, esprimibili attraverso equazioni alle derivate parziali, di notevole importanza nella risoluzione di problemi applicativi. Svariati altri modelli matematici sono oggetto di interesse per la modellistica c.: si pensi, per es., al problema della rappresentazione di curve e superfici, al trattamento numerico di immagini e segnali, alla minimizzazione di funzionali liberi o vincolati, alla regolarizzazione numerica e risoluzione di problemi inversi, ai problemi integro-differenziali, nonché al controllo di sistemi differenziali, integrali o di natura stocastica.

La rilevanza dei metodi c. nell’analisi e simulazione di processi meccanici (nell’analisi strutturale, nella fluidodinamica, nella bioingegneria ecc.), fisici (nella microelettronica, nella propagazione ondosa, nella diffusione dei neutroni), chimici (cinetica e dinamica delle reazioni chimiche), economici (nei sistemi deterministici o statistici per la descrizione di sistemi microeconomici, nei processi di investimento con opzioni) è notevole e destinata a crescere nel tempo.

Convergenza e stabilità

La prima fase della modellistica c. consiste nella sostituzione del modello matematico F(u,d)=0 con un modello numerico F_n(u_n,d_n)=0, dipendente da un parametro n il cui significato varia a seconda della famiglia di problemi considerata, ma che può essere sempre riferito alla dimensione del modello numerico medesimo. In tale contesto, d_n è un’approssimazione di d, F_n una discretizzazione della relazione funzionale F e u_n la soluzione numerica. La proprietà fondamentale che si richiede a un modello numerico è la convergenza, ovvero che u_n→u per n→∞. Condizione necessaria perché ciò avvenga è che F_n traduca correttamente la legge funzionale F, ovvero che F_n(u,d)→0 per n→∞, essendo d un dato ammissibile per il modello matematico e u la corrispondente soluzione. Tale proprietà, detta consistenza, non è peraltro sufficiente a garantire la convergenza della soluzione numerica a quella esatta: a tale scopo serve che il modello numerico sia stabile. Al fine di definire la stabilità, si ricordi che un modello matematico si dice ben posto se ammette una sola soluzione e a piccole perturbazioni dei dati corrispondono variazioni controllabili della soluzione (ossia, è ben condizionato). Più precisamente, se d e d* rappresentano due insiemi di dati, δd=d*−d la loro differenza, u e u* le soluzioni corrispondenti, e δu = u*−u, il problema è ben condizionato se il massimo valore del rapporto fra l’errore relativo sulla soluzione ∥δu∥/∥u∥ e l’errore relativo sui dati ∥δd∥/∥d∥ (avendo indicato con il simbolo ∥ ∥ delle norme opportune) nell’insieme di tutte le perturbazioni ammissibili dei dati è dell’ordine dell’unità; se, invece, il valore di tale rapporto (generalmente denominato numero di condizionamento e indicato con il simbolo K) è molto maggiore dell’unità, il problema si dice mal condizionato. Si supponga che la soluzione u del problema fornita dal modello matematico si possa rappresentare come u=f(d) e analogamente la soluzione del modello numerico si possa ottenere come u_n=f_n(d_n), essendo f e f_n due opportune leggi di corrispondenza. Allora, se f è differenziabile, si ottiene per K la seguente stima: K=∥f′(d)∥∥d∥/∥f(d)∥; analogamente si può associare al modello numerico un numero di condizionamento K_n=∥ f_n′(d_n)∥∥d_n∥/∥f_n(d_n)∥ e definire il numero di condizionamento asintotico del modello numerico (K*) come il massimo valore del limite di K_n per n→∞. È ora possibile precisare il concetto di stabilità numerica: dato un modello matematico ben condizionato con un numero di condizionamento K, la famiglia (dipendente dal parametro n) di modelli numerici è stabile se K* è dello stesso ordine di grandezza di K. In caso contrario si parlerà di modello numerico instabile. La stabilità assicura, in particolare, la limitatezza uniforme (rispetto a n) delle soluzioni numeriche.

Errore c. e metodi adattivi

Il modello matematico, costituendo un tentativo di legare tra loro quantità di interesse ‘fisico’ attraverso relazioni matematiche, spesso semplificate rispetto alla complessità del problema originario, ha una soluzione u che sarà diversa da quella u_f del problema fisico in esame. La differenza e_m=u_f−u dipende sia dalla significatività (e ragionevolezza) delle ipotesi semplificative adottate, sia dall’accuratezza con la quale le quantità fisiche reali sono state rappresentate dall’insieme d dei dati del modello. L’errore e_m è pertanto intrinseco al processo di modellizzazione. Il metodo c. adottato provocherà un altro errore, indicato con e_c, che esprime la distanza fra la soluzione effettivamente calcolata û_n e u. L’errore globale e, differenza fra la reale soluzione fisica u_f e quella calcolata û_n, risulterà dalla combinazione dei due errori, e_m ed e_c. L’obiettivo della modellistica c. è quello di garantire un errore e_c piccolo e controllabile (affidabilità) con il minor costo c. possibile (efficienza).

Per costo c. si intende la quantità di risorse (tempo di calcolo, occupazione di memoria) necessaria per calcolare la soluzione û_n. L’affidabilità è un requisito cruciale di un metodo c.: l’analisi mira a trovare stime dell’errore e_c (in funzione dei dati del problema e dei parametri della discretizzazione), le quali consentano di garantire che esso stia al di sotto di un certo valore fissato a priori. A questo scopo è utile ricorrere ad algoritmi adattivi (o adattativi) che utilizzano una procedura di retroazione (feedback) a partire dai risultati già ottenuti per modificare i parametri della discretizzazione e migliorare la qualità della soluzione. I metodi numerici che attuano una strategia adattiva per il controllo dell’errore sono detti metodi c. adattivi. L’errore c. viene generato per il fatto che, nella fase d della risoluzione del problema, il modello numerico deve essere implementato, sviluppato su un elaboratore con l’ausilio di un algoritmo opportuno. Si producono così nuovi errori, alcuni intrinseci all’algoritmo, altri (errori di arrotondamento, che decrescono esponenzialmente con il numero di cifre significative utilizzato) attribuibili all’aritmetica finita di cui fa uso l’elaboratore per rappresentare i numeri reali ed eseguire operazioni algebriche tra essi. La combinazione di tali errori fornisce l’errore algoritmico e_a=u_n−û_n. L’errore del metodo c. (e_c=u−û_n) è la somma dell’errore numerico (e_n=u−u_n) e di quello algoritmico. L’obiettivo ultimo dell’analisi dell’errore del metodo c. è quello di dimostrare che esso tende a zero per n→∞.

Chimica

Chimica computazionale

Branca della chimica che si occupa da un lato dello sviluppo di nuove procedure di calcolo basate sui principi della meccanica quantistica o della meccanica classica, dall’altro della realizzazione pratica dei calcoli (elaborazione degli algoritmi, scrittura dei programmi di calcolo, configurazione degli elaboratori impiegati per l’esecuzione dei calcoli ecc.). La chimica c. ha ricevuto grande impulso nel corso degli anni 1980 e 1990. L’assegnazione del premio Nobel per la chimica nel 1998 a W. Kohn e J. A. Pople ha in qualche modo sancito ufficialmente l’ingresso di questa disciplina tra le principali branche della chimica accanto a quelle tradizionali. Tale avanzamento è stato reso possibile dallo sviluppo di elaboratori elettronici sempre più veloci e in particolare, a partire degli anni 1990, dalla disponibilità di potenti elaboratori ad architettura parallela, capaci di compiere in tempi ragionevoli calcoli complessi su sistemi molecolari di dimensioni anche notevoli.

I principali campi in cui la chimica c. ha trovato applicazione sono quelli della chimica quantistica propriamente detta, della meccanica molecolare e della dinamica molecolare.

Chimica quantistica

I metodi di questa disciplina permettono di calcolare la struttura geometrica ed elettronica delle molecole, i loro moti rotazionali e vibrazionali, le loro proprietà ottiche e magnetiche ecc. I tipi di calcolo impiegati sono usualmente suddivisi in calcoli ab initio e calcoli semiempirici. Entrambi si basano sull’applicazione diretta delle leggi fondamentali della meccanica quantistica, ma quelli semiempirici, a differenza di quelli ab initio, fanno uso di parametrizzazioni suggerite da dati sperimentali, allo scopo di diminuire la potenza di calcolo necessaria. Questa, infatti, aumenta rapidamente al crescere della complessità dei sistemi molecolari studiati e dell’accuratezza richiesta.

Un’approssimazione su cui poggia una buona parte dei calcoli chimici è l’approssimazione di Born-Oppenheimer, che consiste nel trascurare il moto dei nuclei. In tal modo, il principale problema da risolvere per studiare la struttura di una molecola sta nella risoluzione dell’equazione di Schrödinger (➔) a molti elettroni per una data geometria molecolare (cioè per fissate posizioni dei nuclei). Il calcolo viene poi ripetuto modificando di volta in volta la geometria.

Tra i metodi di calcolo della chimica quantistica, ormai classico è il metodo (o approssimazione) di Hartree-Fock. Esso permette di ridurre il problema della risoluzione dell’equazione di Schrödinger a molti elettroni a quello della risoluzione di un sistema di equazioni monoelettroniche, in cui ogni elettrone risente semplicemente del potenziale (campo medio) dovuto a tutti gli altri elettroni. Tale approccio soffre di numerose limitazioni; in particolare, non descrive la cosiddetta correlazione elettronica, cioè la repulsione puntuale (non media) tra gli elettroni. Tra i numerosi metodi sviluppati per ottenere risultati più accurati vi è il metodo della interazione di configurazione (CI, configuration interaction), nel quale lo stato fondamentale del sistema viene descritto mescolando varie configurazioni elettroniche, cioè introducendo diverse funzioni di stato multielettroniche ‘eccitate’. Un altro metodo che ha trovato grande diffusione a partire soprattutto dagli anni 1980 è la teoria del funzionale della densità (DFT, density functional theory), basata sul fatto che l’energia dello stato fondamentale di una molecola si può esprimere come funzionale della densità elettronica totale. Il problema si sposta perciò al calcolo di questa grandezza. Il metodo DFT, nelle sue numerose varianti, ha il vantaggio di richiedere potenze di calcolo inferiori rispetto ai metodi ab initio classici, fornendo spesso risultati di accuratezza confrontabile.

Meccanica molecolare

In questo approccio la molecola è descritta in modo assai semplificato, come un insieme di sfere rigide (nuclei) tenute insieme da molle (legami). Il metodo si basa sull’uso di funzioni di potenziale derivate dalla meccanica classica per descrivere l’energia complessiva della molecola. La funzione di energia potenziale è data dalla somma di vari termini, ciascuno dei quali rappresenta il potenziale associato a uno o più legami (potenziali di stretching, bending, torsioni). Nel calcolo sono inseriti anche termini che descrivono le interazioni fra atomi non direttamente legati (interazioni di van der Waals, coulombiane, legami idrogeno). I singoli potenziali sono valutati utilizzando parametri sperimentali quali costanti di forza, lunghezze e angoli di legame, angoli di torsione. Pur basandosi su una descrizione assai meno realistica rispetto a quella quantistica, la meccanica molecolare ha riscosso un grande successo per la sua capacità di fornire, con sforzo c. modesto, informazioni strutturali importanti (soprattutto geometrie molecolari) per molecole di grandi dimensioni (proteine, acidi nucleici) non trattabili con i metodi della chimica quantistica. Sono stati anche sviluppati dei metodi misti: così una molecola organica complessa può essere trattata, nel suo insieme, mediante la meccanica molecolare, mentre una sua particolare porzione, responsabile, per es., di determinate funzioni biologiche, può essere trattata in modo più accurato con un metodo ab initio.

Dinamica molecolare

fig. 2

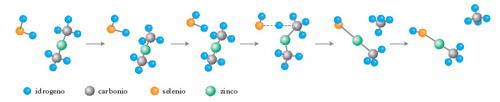
È la terza categoria di metodi c. in chimica. I calcoli di dinamica molecolare (➔ dinamica) permettono di studiare le proprietà di sistemi allo stato liquido e di molecole o macromolecole in soluzione e simulare l’andamento di reazioni chimiche (fig. 2).

Fisica

Metodi c. e fisica

La metodologia c. è ampiamente impiegata in molte aree della fisica, sia fondamentale, sia applicata. Fra le applicazioni pionieristiche vanno citati gli studi di E. Fermi, J. Pasta e S.M. Ulam (1953) sull’evoluzione verso l’equilibrio di sistemi di oscillatori non lineari, e studi di termodinamica con il metodo statistico montecarlo di N. Metropolis (1947), secondo uno schema proposto alcuni anni prima da Fermi. Un altro ormai celebre risultato c. riguarda la scoperta del cosiddetto caos deterministico, dovuta al meteorologo E. Lorenz (1963). Metodi c. ebbero immediato impiego in problemi di fisica applicata riguardanti, per es., la fisica dei reattori a fissione e la fisica degli armamenti nucleari e, poco dopo, nella simulazione evolutiva di problemi complessi, il cui studio richiede la trattazione simultanea di molteplici fenomeni elementari, quali quelli che s’incontrano nell’evoluzione stellare, nella dinamica dell’atmosfera, nella climatologia ecc. Grande sviluppo hanno avuto successivamente le tecniche c. in fluidodinamica e aerodinamica (sia per lo studio di aspetti di natura fondamentale, quali i moti turbolenti, sia per le applicazioni, alla progettazione aeronautica, navale ecc.), in fisica della materia condensata, in fisica delle interazioni forti (cromodinamica quantistica sul reticolo) e nello studio dei sistemi dinamici in generale.

Tipologie di modelli e applicazioni

Molti fenomeni possono essere trattati nell’ambito della fisica dei sistemi continui, per es. descritti da sistemi di equazioni alle derivate parziali (equazioni di Navier-Stokes per un fluido, o le equazioni del modello magnetofluidodinamico di un plasma). In questi casi l’approccio c. è spesso basato sulla discretizzazione di dette equazioni (per es. alle differenze finite, o agli elementi finiti) su una maglia costituita da un certo numero di punti opportunamente disposti e consente di ottenere soluzioni numeriche approssimate della distribuzione nello spazio e nel tempo delle grandezze fisiche rilevanti. È possibile introdurre in tali schemi dati relativi alle proprietà locali dei materiali, agli scambi energetici, alle condizioni iniziali (se si tratta di problemi evolutivi) o al bordo del sistema. Modelli di tal tipo sono ampiamente impiegati, fra l’altro, oltre che in fluidodinamica e meccanica dei sistemi continui, in meteorologia, climatologia, astrofisica, fisica della fusione nucleare ecc. In alternativa ai metodi di discretizzazione, possono essere impiegati, qualora le condizioni al bordo lo consentano, metodi spettrali (basati, per es., sulla trasformata di Fourier delle equazioni del modello).

Lo studio delle proprietà atomiche dei materiali richiede modelli che includano descrizioni accurate delle interazioni fra i singoli costituenti elementari (elettroni e nuclei). In questo caso lo studio c. si effettua studiando in modo dettagliato un sottosistema abbastanza grande da poter ritenere che mostri le stesse proprietà di un campione macroscopico di materia, ma sufficientemente piccolo da consentire la soluzione delle equazioni relative alle interazioni mutue fra tutti i componenti.

In altri casi ancora, per studiare il comportamento di un’ampia ‘popolazione’ (per es., per studiare la funzione di distribuzione di fascio di particelle che si propaga all’interno di un dato sistema, la distribuzione di un inquinante in un fluido, la distribuzione attesa di determinati eventi in un rivelatore di particelle), si simula in modo dettagliato l’evoluzione di un sottoinsieme della popolazione stessa, al fine di ricostruire in modo approssimato la distribuzione che si intende studiare. A seconda dei casi, il singolo ‘elemento’ della popolazione è studiato con metodi deterministici (come nel caso del moto di particelle cariche in un plasma non collisionale, o del moto di stelle in ammassi stellari), oppure con metodi probabilistici (metodi montecarlo). Questi sono impiegati per la trattazione di eventi elementari descritti da leggi statistiche (quali, per es., assorbimento o emissione di un fotone, scattering di particelle ecc.). Sono anche spesso usate combinazioni dei metodi precedenti. Ne sono esempio i cosiddetti metodi a particella-in-cella, usati in fisica dei plasmi, in cui si simula un insieme limitato di particelle campione. A ogni passo temporale (discreto) della simulazione, dalla distribuzione delle particelle e delle loro velocità si ottengono le densità di carica e corrente su una maglia spaziale, su cui vengono risolte le equazioni dei campi, a loro volta impiegati per effettuare lo spostamento delle particelle nel passo successivo.

Linguistica

La linguistica c. è un settore di recente sviluppo, che ha come oggetto di studio gli aspetti quantificabili del linguaggio e delle lingue: frequenza e quantità di informazione di ciascun elemento, restrizioni e regole di tipo morfologico e sintattico, traduzione automatica. Centri avanzati di linguistica c. sono attivi negli Stati Uniti e in Gran Bretagna, ma anche in Italia, a Pisa, dove va segnalato l’Istituto di linguistica computazionale Antonio Zampolli, fondato come istituto indipendente del Consiglio Nazionale delle Ricerche nel 1978.

Abstract di approfondimento da Chimica computazionale di Sergio Carrà (Enciclopedia della Scienza e della Tecnica)

La prospettiva di poter descrivere i fenomeni chimici mediante calcoli è affiorata, in termini concreti, nella prima metà del Novecento con l’avvento della meccanica quantistica. Infatti, dopo essere passata attraverso una fase di definizione concettuale, che ha ridisegnato il volto della chimica, ormai la meccanica quantistica è entrata in una fase operativa tale da essere in grado di valutare con accuratezza la struttura e l’energia delle molecole, sia quando sono isolate, sia quando collidono per dare origine a nuovi composti. Il riconoscimento del grande progresso così conseguito è testimoniato dall’attribuzione, nel 1998, del premio Nobel per la chimica a due scienziati, Walther Kohn e John A. Pople, per le loro ricerche sulla teoria del funzionale della densità e per lo sviluppo di metodi computazionali. Anche se l’approccio computazionale può sembrare troppo illuministico, in quanto sembra intaccare il tradizionale carattere sperimentale della chimica, esso, in realtà, sta acquistando un ruolo sempre più rilevante anche in numerosi settori scientifici e tecnologici connessi con questa scienza.

Infatti, se fino a qualche anno fa i chimici teorici si dovevano accontentare di riprodurre dati sperimentali già noti, attualmente essi possono avventurarsi – seppure con cautela – nella previsione di dati utili per orientare le indagini nei casi in cui le informazioni sperimentali dettagliate siano carenti. In particolare queste possibilità si verificano in campi come quello delle sintesi chimiche, dei processi di combustione, della catalisi, della chimica ambientale e atmosferica, della preparazione di materiali tecnologicamente avanzati, della biologia molecolare, della chimica cosmica e di altri ancora. La sinergia fra risultati sperimentali sempre più accurati riguardo la struttura e la dinamica delle molecole, e la loro interpretazione mediante dettagliati calcoli teorici, sta conferendo alla chimica un rinnovato slancio, non solo sul piano concettuale, ma anche nelle applicazioni su tematiche di frontiera.

È interessante osservare come la prospettiva di sviluppo di una concreta chimica computazionale fosse già stata preconizzata da Paul-Adrien-Maurice Dirac, uno dei padri della meccanica quantistica, quando nel 1929 affermava che «le leggi fisiche fondamentali necessarie per la teoria ;matematica dell’intera chimica sono ormai completamente note, e la difficoltà è dovuta solo al fatto che la loro applicazione porta a equazioni troppo complicate per essere solubili». Secondo Pople, l’esame retrospettivo della frase precedente appare «come un grido di trionfo e di disperazione», poiché essa preannunciava l’avvento di un colossale sforzo matematico. In questo senso la chimica computazionale si può allora considerare come la realizzazione – in parte conseguita ma ancora in via di svolgimento – del programma implicitamente enunciato da Dirac.

In realtà, la rilevanza che sta acquistando la chimica computazionale trae vantaggio anche dallo sviluppo di metodologie e tecniche sperimentali che permettono di ottenere informazioni sempre più accurate sulla struttura delle molecole, sulle transizioni energetiche cui sono soggette e sulla dinamica dei loro movimenti derivanti dalle interazioni con le altre molecole. In questo quadro meritano di essere menzionati i risultati ottenuti mediante l’impiego del laser, che grazie alla produzione di impulsi dell’ordine dei femtosecondi permettono di cogliere le caratteristiche geometriche e dinamiche dei complessi molecolari che si formano all’atto di collisione dei reagenti stessi.