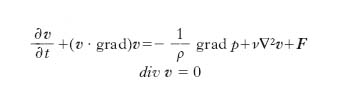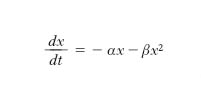turbolenza

turbolenza Comportamento irregolare e impredicibile dei fluidi in certe condizioni. Il termine indica anche, in un contesto più vasto, il moto caotico presente in sistemi dinamici deterministici dissipativi con un attrattore strano nello spazio delle fasi (quindi anche in chimica, in ottica ecc.).

Fisica

In fluidodinamica, condizione di flusso di un fluido (flusso turbolento) in cui il moto delle particelle varia nello spazio e nel tempo in modo irregolare, con elevate fluttuazioni del campo di velocità e valori medi delle varie grandezze funzioni, in genere continue, dei parametri da cui il moto stesso dipende.

L’evoluzione di un fluido è descritta dalle equazioni di Navier-Stokes, che nel caso di flusso incompressibile si scrivono:

dove v è il campo di velocità, p la pressione, F la forza esterna agente sull’unità di massa, ρ la densità del fluido e ν la sua viscosità cinematica. Fissata la geometria del sistema, l’unico parametro rilevante è il numero di Reynolds, R_e=VL/ν (in cui V e L sono velocità e dimensione lineare caratteristica), rapporto tra il valore tipico del termine non lineare (v∙grad)v, di ordine V²/L, e di quello lineare ν∇²v, di ordine νV/L². Per valori piccoli di R_e si ha un comportamento regolare (moto laminare); per valori di R_e dell’ordine di 100 si passa a un moto con strutture spazialmente ben organizzate, ma con un’evoluzione temporalmente caotica (t. debole). Al crescere di R_e le strutture spaziali diventano sempre più complesse e coinvolgono scale spaziali sempre più piccole (t. sviluppata o completamente sviluppata). Un esempio di t. è dato dal getto d’acqua che esce da un rubinetto; la viscosità e le dimensioni del rubinetto sono fissate e R_e è proporzionale alla portata. Aprendo solo un po’ il rubinetto l’acqua scende in modo regolare e la forma del filetto fluido non cambia nel tempo (moto laminare). Aumentando la portata, il moto appare complicato e variabile da punto a punto e la forma del filetto fluido non è costante.

Nella t. si hanno 2 classi di problemi: a) la transizione dal moto laminare al comportamento caotico (transizione alla t., o innesco della t. o transizione al caos): per valori di R_e non troppo grandi le strutture spaziali sono ben organizzate, i gradi di libertà coinvolti sono pochi e si ha solo caos temporale; b) la t. sviluppata: per valori di R_e molto grandi i gradi di libertà sono molti e si ha comportamento irregolare sia nel tempo che nello spazio.

Transizione alla turbolenza

In generale il parametro di controllo r, al variare del quale si passa da un comportamento regolare fino alla t. sviluppata, dipende dal problema specifico. Per es., in un flusso incompressibile r è Re e nel moto convettivo di un fluido tra due piani orizzontali, riscaldato dal basso, è il numero di Rayleigh, proporzionale alla differenza della temperatura tra i due piani. Nel seguito sono descritti i principali meccanismi per l’innesco della t. nei fluidi, ovvero i differenti scenari di transizione al caos proposti da L. Landau e E. Hopf, D. Ruelle e F. Takens, M. Feigenbaum, Y. Pomeau e P. Manneville. Nello schema di Landau e Hopf il comportamento caotico è prodotto dalla sovrapposizione di un certo numero (crescente con r) di oscillazioni regolari di frequenza diversa, in rapporti non razionali. Ruelle e Takens hanno dimostrato che tale meccanismo non può valere oltre la transizione da 2 a 3 frequenze, non essendo quella da 3 a 4 frequenze strutturalmente stabile. Della teoria di Landau e Hopf, essi mantengono solo i primi 3 passaggi (transizione da punto fisso a ciclo limite, da ciclo limite a traiettoria con due frequenze, da traiettoria con 2 frequenze a traiettoria con 3 frequenze) e ipotizzano poi il passaggio da una traiettoria con 3 frequenze a un attrattore strano, cioè con forte dipendenza dalle condizioni iniziali (➔ caos, predicibilità). Lo scenario di Landau e Hopf richiede molti gradi di libertà, mentre quello di Ruelle e Takens può generare il caos anche con un’equazione differenziale con tre gradi di libertà. Il meccanismo di Feigenbaum (raddoppio del periodo) si basa sulle proprietà frattali del diagramma di biforcazione, tipiche, come egli stesso dimostra, delle mappe unidimensionali della forma x(t+1)=gr(x(t)), in cui la funzione gr(x) ha un solo massimo di tipo quadratico (intorno al quale è approssimabile con una parabola); ciò assicura l’esistenza, per una vasta classe di leggi di evoluzione, di un meccanismo universale di transizione al caos indipendente dalla forma dettagliata della gr(x). Lo scenario di Pomeau e Manneville nasce dall’osservazione del comportamento, detto intermittente, presente in alcuni fenomeni chimici e fluidodinamici. Per r<rc, dove rc è un valore critico, l’evoluzione di un sistema intermittente è regolare, mentre per r=rc+ε, con ε>0 piccolo, si ha un lungo intervallo di tempo di comportamento regolare seguito da una fase ‘turbolenta’ e da un altro lungo intervallo regolare, in genere di durata diversa. La durata media della fase laminare è proporzionale a 1/√--ε. Un esempio è fornito da una mappa x(t+1)=gr(x(t)), in cui per r<rc, gr(x) interseca la bisettrice del primo quadrante in due punti stabili, per r=rc il grafico di gr(x) è tangente alla bisettrice del primo quadrante, mentre per r>rc la distanza minima del grafico di gr(x) dalla bisettrice è di ordine r−rc. I meccanismi proposti hanno dunque le seguenti caratteristiche: a) Landau-Hopf, per r=r1, r2, r3, ... rn, rn+1, ... (con rn crescenti e non limitati) si hanno le transizioni punto fisso → soluzione periodica con una frequenza → soluzione periodica con 2 frequenze →…→ soluzione periodica con n frequenze →…→ soluzione periodica con n+1 frequenze →…; b) Ruelle-Takens, per r=r1, r2, r3, r4 si ha punto fisso → soluzione periodica con una frequenza→ soluzione periodica con 2 frequenze → soluzione periodica con 3 frequenze → attrattore strano (soluzione periodica); c) Feigenbaum, per r=r1, r2, r3,

, r_n, r_n+1, ..., con r_n crescenti e lim_n→∞ r_n = r_c,

si ha punto fisso → soluzione periodica con periodo 2 → soluzione periodica con periodo 4 →…→ soluzione aperiodica con periodo 2ⁿ → soluzione periodica con periodo 2ⁿ⁺¹ …→ caos (per r>r_c); d) Pomeau-Manneville, si ha un solo valore critico r_c a cui avviene la transizione punto fisso → soluzione aperiodica intermittente. Gli scenari b), c) e d) si sono osservati sia numericamente sia sperimentalmente; per es., sono stati molto studiati: l’instabilità nei laser, la convezione di Rayleigh-Bénard, il moto di Couette (o di Taylor-Couette) generato in un fluido contenuto tra due cilindri rotanti in versi opposti intorno al loro asse comune. A partire da un segnale v(t) con 0<t<T (per es., la velocità o la temperatura misurate in un punto) calcolando lo spettro di potenza S(f), definito dalla

relazione S(f)=∣(1/T)∫^T₀ v(t)e^i2πftdt∣², si

può capire quali meccanismi di transizione sono operanti. Se v(t) è dato dalla sovrapposizione di termini sinusoidali con r₁<r<r₂, S(f) mostrerà un solo picco, in corrispondenza della frequenza f₁; se r₂<r<r₃, S(f), mostrerà due righe in corrispondenza di f₁ e f₂ ecc. Se lo scenario di Landau e Hopf fosse adeguato a descrivere i fenomeni di t., S(f) sarebbe costituito da sole righe sempre più numerose al crescere di r. Nello spettro di potenza si osserva invece, per r>r_c, una componente continua, come previsto dagli altri tre scenari.

Il meccanismo di transizione alla t. non è unico ma dipende dal sistema in esame. Lo scenario di Ruelle-Takens è stato osservato nella convezione di Rayleigh-Bénard, per fluidi con alti numeri di Prandtl, e nel moto di Couette. Lo scenario di Feigenbaum si osserva nei laser, nella reazione chimica di Belousov-Žabotinskij, per certi valori delle concentrazioni, e nella convezione di Rayleigh-Bénard, per fluidi con piccoli numeri di Prandtl (nel mercurio). Lo scenario di Pomeau-Manneville si manifesta ancora nella reazione di Belousov-Žabotinskij, per altri valori delle concentrazioni, e nella convezione di Rayleigh-Bénard in certe situazioni. Anche se il meccanismo di transizione al caos non è universale, il numero degli scenari non è molto alto. È chiaro inoltre che non si ha mai un meccanismo tipo Landau e Hopf, mentre nel passaggio dall’ordine al caos si ha sempre un attrattore strano a bassa dimensionalità.

T. sviluppata

Il problema della t. sviluppata, di grande importanza applicativa (meteorologia, ingegneria aeronautica ecc.), è centrale anche nella fisica teorica in connessione con lo studio dei fenomeni che presentano invarianza nei cambiamenti di scala. Un’analisi numerica delle equazioni di Navier-Stokes ad alto numero di Reynolds presenta difficoltà notevoli: argomenti di tipo dimensionale mostrano che il numero di gradi di libertà da considerare cresce come Re9/4, mentre il passo di integrazione numerica deve essere proporzionale a Re−1/2; perciò il numero di operazioni necessarie per simulare un flusso turbolento su un dato intervallo di tempo aumenta come Re13/4. Per i molti gradi di libertà coinvolti, nella t. sviluppata non si descrive dettagliatamente il campo di velocità, ma lo si tratta come una variabile stocastica e non come una variabile completamente determinata dalle condizioni iniziali e al contorno, limitandosi a una teoria statistica della turbolenza. Si considera il flusso incompressibile omogeneo e isotropo in uno stato statisticamente stazionario, in modo che medie spaziali e temporali coincidano con le medie prese su un insieme di copie ideali del sistema fisico a parità dei parametri esterni, quali Re e le condizioni al contorno. Nel caso di fluido perfetto con viscosità ν=0, si può costruire una meccanica statistica analogamente al caso dei gas: mediante la legge di conservazione e l’invarianza del volume nello spazio delle fasi si ottiene una distribuzione gaussiana per il campo di velocità. Il limite ν→0 (equivalente a Re→∞) è però singolare e la statistica della t. sviluppata non ha nessuna relazione con quella ottenuta per un fluido perfetto.

Le componenti della velocità in un dato punto, misurate per es. con un anemometro a filo caldo, hanno distribuzione pressoché gaussiana, mentre quantità che coinvolgono più punti presentano una statistica più complessa. La quantità più semplice da studiare è la differenza di velocità δv fra due punti; tipicamente, posto r=(1,0,0), si ha per la componente longitudinale δvL(x, r)=vL(x+r)− vL(x). La statistica di δv non è gaussiana e ciò ha un ruolo centrale nella teoria della turbolenza. Una descrizione statistica della t. si può effettuare considerando delle equazioni differenziali per le medie a uno e a più punti, ottenendo delle equazioni differenziali ordinarie al posto di una alle derivate parziali, dovendo però risolvere il problema della chiusura, dovuto alla natura non lineare delle equazioni di Navier-Stokes. Il problema si può illustrare in un’equazione differenziale ordinaria a una variabile,

con α e β costanti, di struttura simile alle equazioni di Navier-Stokes (termini non lineari quadratici). Se si vuole calcolare l’evoluzione dei momenti Mj(t)=‹xj(t)› (dove ‹ › indica la media e j=1, 2, 3, ...) dalla conoscenza del loro valore Mj(0) all’istante iniziale t=0, mediando la [1], si ottiene l’equazione per il momento di ordine uno: dM1/dt=−αM1−βM2; questa contiene il momento di ordine due per il quale si può ottenere, sempre dalla [1], (1/2)dM2/dt=−αM2−βM3. Scrivendo l’equazione per M3 comparirà M4 e così via. A qualunque livello ci si trovi, il numero di variabili supera di un’unità quello delle equazioni. Va perciò fatta un’ipotesi ragionevole sul momento di un certo ordine per chiudere la catena di equazioni. Per es., ponendo M2 proporzionale a M33/2, si resta con due sole equazioni. Nella t., gli approcci più semplici per chiudere le equazioni, come assumere che la statistica sia quasi gaussiana, portano a risultati deludenti. Non sembra possibile affrontare il problema partendo da principi primi e bisogna limitarsi a chiudere il sistema di equazioni con argomenti euristici. Risultati sperimentali e considerazioni qualitative permettono di ricavare alcuni aspetti della statistica a piccola scala. In particolare, il momento terzo di δv risulta negativo, mentre se la distribuzione fosse gaussiana sarebbe nullo. Questo momento, in 3 dimensioni, entra nell’equazione per il momento secondo, connesso con la densità di energia, ed è responsabile del passaggio dell’energia dalle grandi scale alle piccole scale, in un processo, ipotizzato da L.F. Richardson nel 1922, detto cascata dell’energia. In essa si assume un trasferimento di energia (dovuto al termine non lineare delle equazioni di Navier-Stokes) dalle strutture vorticose sulla scala L, caratteristica del sistema, che assorbono energia dalla forza esterna, alle strutture su scale via via più piccole, fino alla scala lD ~LRe-1/3 (lunghezza di Kolmogorov), in cui il termine lineare viscoso delle equazioni di Navier-Stokes domina la dinamica, il trasferimento a cascata cessa e l’energia è dissipata in calore. La cascata è congetturata in base a argomenti fenomenologici e sostenuta da simulazioni numeriche, ma non è derivata dalle equazioni di Navier-Stokes. L’ipotesi della cascata permette di intuire i meccanismi fondamentali che avvengono in un flusso turbolento ed è compatibile con l’invarianza di scala che appare nelle equazioni di Navier-Stokes quando il numero di Reynolds va all’infinito. In questo caso, corrispondente al tendere a zero della viscosità, le equazioni risultano invarianti sotto dilatazioni delle lunghezze: r→λr, con λ reale positivo, quando si trasformino simultaneamente anche le velocità e il tempo: v→λhv, t→λ1-ht. L’esponente h non si può però determinare da considerazioni di simmetria. Ci si aspetta che, nei fluidi incompressibili, le proprietà statistiche della t. alle piccole scale di lunghezza seguano leggi di scala universali, indipendenti da condizioni al contorno, tipo di fluido o forzamento esterno, e che gli esponenti di queste leggi si possano calcolare in base all’ipotesi della cascata di energia.

Nel 1941 A.N. Kolmogorov ha proposto una teoria della t. fondata su un’ipotesi di invarianza di scala globale, per cui, nel processo a cascata, il tasso di trasferimento dell’energia non dipende dalla scala di lunghezza l, nell’intervallo [lD, L] (detto inerziale, in quanto dominato dalle forze di inerzia), e la densità di energia dissipata nell’unità di tempo, ε(x), è uniforme nello spazio. Mediante argomenti dimensionali, Kolmogorov formulò le leggi di scala per le differenze di velocità δvx(l)=∣v(x + r)−v(x)∣, con il modulo di r di ordine l, e precisamente: δvx(l)~lh, con h=1/3 per ogni punto x del fluido. La validità della teoria si verifica sperimentalmente studiando l’andamento delle funzioni di struttura (cioè i valori medi dei momenti delle differenze di velocità) al variare di l: ‹δvx(l)p›~lζp. L’invarianza di scala globale implica ζp=p/3. Al contrario, i dati sperimentali mostrano degli scostamenti da questa predizione, e ζp pare non essere una funzione lineare di p. La rottura dell’invarianza di scala globale risulta evidente osservando gli effetti dovuti alle fluttuazioni della dissipazione dell’energia ε(x). Le simulazioni numeriche mostrano che l’energia non si dissipa uniformemente ma su strutture filiformi di tipo frattale.

Gli argomenti dimensionali alla Kolmogorov sono stati ripresi da B.B. Mandelbrot con l’ipotesi che la dissipazione dell’energia non sia omogenea nello spazio, ma sia distribuita uniformemente su un frattale di dimensione frattale DF<3 (dai dati sperimentali si stima DF=2,8). Ne risulta che δvx~l, cioè h=1, se x non appartiene al frattale, mentre h=(DF−2)/3 se x appartiene al frattale. Poiché il volume della struttura frattale è proporzionale a lDF, solo una frazione l3−DF del fluido è ‘attiva’ su scala l e, per le funzioni di struttura, si ha ζp=3− DF+p(DF−2)/3.

Questo risultato non giustifica ancora i dati sperimentali, da cui risulta che ζp è funzione non lineare di p. Perciò, anche l’ipotesi di dissipazione di energia omogenea su una struttura frattale va abbandonata e va ipotizzata un’invarianza di scala locale, ammettendo che l’esponente h vari all’interno di uno spettro continuo di valori, caratterizzati da una distribuzione di probabilità P(h). L’insieme frattale va visto come un multifrattale, unione di insiemi frattali omogenei S(h), dove S(h) è il sottoinsieme dei punti del fluido caratterizzati dallo stesso esponente h e risulta esso stesso un frattale di dimensione D(h)≤DF. Calcolando le funzioni di struttura, in questo caso si ha: ζp=minp [hp−D(h)+3], relazione che mostra come leggi di scala ‘anomale’ (non lineari in p) per i momenti delle differenze di velocità siano in relazione a un’ipotesi di invarianza di scala locale piuttosto che globale. Il valore h=1/3 della teoria di Kolmogorov corrisponde al caso limite di dissipazione su un insieme non frattale tridimensionale. Il modello multifrattale fornisce previsioni quantitative dettagliate su molti aspetti della t., ben verificate sperimentalmente, pur mancando ancora una teoria che derivi lo spettro multifrattale direttamente dalle equazioni di Navier-Stokes.

Lo studio della t. nei fluidi in due dimensioni, oltre che da un punto di vista matematico, è di interesse per comprendere alcuni fenomeni nell’atmosfera, negli oceani e nella magnetosfera. Poiché in due dimensioni, nel limite di fluido non viscoso, la vorticità di ogni particella fluida si conserva, non si può avere una cascata di energia dalle grandi alle piccole scale; è congetturata invece una cascata di enstrofia (quadrato della vorticità). Procedendo come nel caso tridimensionale, si hanno predizioni sullo spettro di potenza dell’energia; ma in due dimensioni gli argomenti dimensionali sono più deboli e le simulazioni numeriche mostrano grandi deviazioni dalle predizioni.

Meteorologia

Nubi di t. Nubi di tipo cumuliforme che si formano quando si ha rimescolamento di strati d’aria con differenti caratteristiche di umidità, temperatura ecc.: la loro formazione è favorita da sbalzi di vento in direzione verticale, elevata umidità relativa, scarsa stabilità atmosferica.