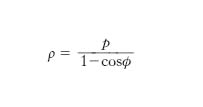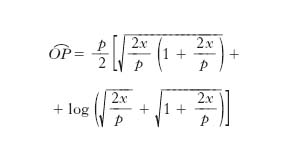parabola

Letteratura

Narrazione di un fatto immaginario ma appartenente alla vita reale, con il quale si vuole adombrare una verità o illustrare un insegnamento morale o religioso; nell’ebraismo rabbinico la p. era molto comune nella predicazione e nell’insegnamento e fu questa appunto la forma originale dell’insegnamento di Gesù. Il termine è riferito oggi esclusivamente alle 49 p. contenute nei Vangeli sinottici.

Matematica

Curva piana, appartenente alla famiglia delle coniche, ottenuta come intersezione della superficie di un cono rotondo indefinito con un piano parallelo a una sola delle sue generatrici.

fig. 1

In geometria, la p. propriamente detta, o p. del 2° ordine (fig. 1), è una conica aperta, costituita da un solo ramo che si prolunga all’infinito, ed è rappresentata in coordinate cartesiane x, y dall’equazione di 2° grado

[1] formula,

nella quale sia

[2] formula.

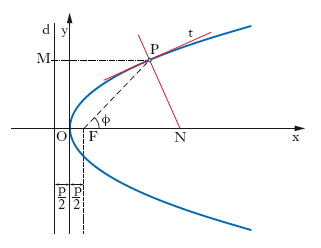
La relazione [2] esprime il fatto geometrico secondo il quale la p. è tangente alla retta impropria, e dunque ha due punti all’infinito reali e coincidenti. Dal punto di vista proiettivo, la p. è invece una curva chiusa, così come l’ellisse e l’iperbole; essa non possiede però un centro di simmetria (è una conica non a centro, contrariamente all’iperbole e all’ellisse), ma possiede un asse di simmetria (in fig. 1 l’asse delle x), che ha lo stesso punto improprio (ossia la stessa direzione) della p., e che la incontra in un unico punto al finito, detto vertice della p. (l’origine O; fig. 1). Se si assume come asse delle x l’asse della p. e come origine il vertice, l’equazione della p. si riduce a una forma particolarmente semplice (equazione canonica): y²=2px. Il numero reale p si chiama parametro della p.: se esso è positivo la p. rivolge la concavità verso destra, cioè nel verso delle x positive, se è negativo verso sinistra, cioè nel verso opposto. Il punto F dell’asse delle x avente dal vertice la distanza p/2 è il fuoco della p.; la retta d parallela all’asse delle y di equazione x=−p/2 è la direttrice. La p. ha eccentricità e=1: essa è il luogo dei punti P per cui la distanza PF dal fuoco e quella PM dalla direttrice sono uguali. L’equazione polare è:

,

dove si convenga di assumere il fuoco come polo e l’asse della p. come asse polare (fig. 1).

La lunghezza dell’arco OP⁀ di p. in funzione dell’ascissa x del suo estremo P è data da:

fig. 2

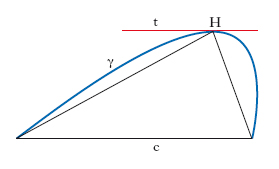
Il raggio di curvatura della p. nel generico punto P è dato da R = n³/p² ove n indica la lunghezza della normale, PN, alla parabola nel punto P. Il segmento di p., cioè (fig. 2) la regione piana compresa tra un arco γ di p. e la corda c che lo sottende, ha area uguale a 4/3 di quella del triangolo che ha per base la corda c, detta base del segmento di p., e il vertice opposto alla base nel punto H di contatto della tangente t alla p. parallela a questa base: è un risultato di Archimede.

fig. 3

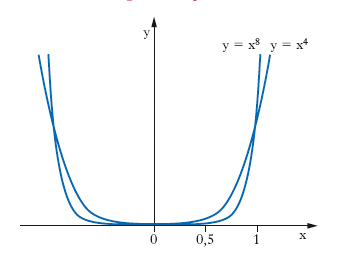
Si chiama p. di ordine n (fig. 3) ogni curva di equazione cartesiana:

Il nome p. è dato anche alle curve di equazione: y^m = pxⁿ (p costante), tra le quali è particolarmente notevole la p. semicubica, di equazione y³ = px², rettificabile elementarmente. Essa è la curva di «abbassamento uniforme» (descensus aequabilis), cioè la curva tale che un punto pesante, abbandonato a sé stesso lungo di essa senza attrito, si abbassa di spazi proporzionali nel tempo (C. Huygens). I. Newton (1706) chiamò p. i 5 tipi di curve del 3° ordine ai quali egli ridusse, per mezzo di proiezioni, ogni possibile cubica piana.