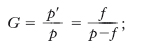specchio
specchio Lastra di vetro alla quale, tramite un processo di verniciatura, viene fatto aderire un sottile strato metallico la cui superficie lucida, che è vista attraverso la lastra stessa, riflette la luce e fornisce quindi un’immagine riflessa degli oggetti illuminati.
Archeologia e arte
I più antichi s. noti sono egiziani; come simbolo del Sole erano sacri ed ebbero la maggiore diffusione nel medio Impero. Sono costituiti da disco metallico, di forme varie, con superficie per lo più convessa, decorati sul verso da scene figurate. I manici sono di legno o di metallo. Anche gli s. micenei hanno disco di bronzo circolare e manico di legno, osso o avorio. Nel mondo greco gli s. più antichi erano di metallo (bronzo), mentre s. di vetro, poco diffusi, comparvero più tardi (età tolemaica): si ottenevano apponendo sul retro di un disco vitreo soffiato una foglia d’oro, di stagno o, più spesso, di piombo. Gli s. greci, oltre che a manico (fuso o di riporto, anche con complessi elementi di raccordo, a volute, palmette o soggetti figurati), possono essere a sostegno (6°-5° sec. a.C.), costituito da una figura o da un motivo architettonico, unito al disco da vari elementi ornamentali, o a scatola (specie 4°-3° sec. a.C.), costituiti da due pezzi uniti da cerniera, che chiudono un disco piatto o fungono, nelle facce interne, da superfici riflettenti.
La produzione etrusca degli s. (6°-2° sec. a.C.; a sostegno ma soprattutto a manico) ha caratteri tipicamente locali, con decorazioni incise, più raramente a rilievo (scene mitologiche, erotiche e di genere, spesso corredate di iscrizioni). Un gruppo stilisticamente ben definito è costituito dagli s. prenestini con iscrizioni latine. Gli s. romani seguono nella forma i greci e gli etruschi; di età romana sono gli s. di vetro incolore, unito a una foglia di piombo, stagno o, più raramente, d’oro.
S. di vetro foderati di metallo furono adoperati durante il Medioevo; s. metallici si usarono fino al Rinascimento, con custodie di legno, avorio, o metallo prezioso. Sin dal 14° sec., e nel 15° soprattutto a Norimberga, furono introdotti s. convessi: all’interno della bolla di vetro ancora calda era immessa una miscela metallica con resina o sale di tartaro; dalla bolla erano poi tagliati specchi dal profilo circolare, inseriti in cornici più o meno elaborate. All’inizio del 16° sec. a Venezia iniziò la produzione di s. piani, di vetro in lastra, ricoperto da un amalgama di stagno e mercurio. Alla produzione veneziana, diffusa in tutta Europa, si affiancò, dal 1665, quella francese della Manifacture royale des glaces, che perfezionò la tecnica del vetro in lastra; più tardi comparvero analoghe fabbriche in Spagna e in Inghilterra. S. artistici di bronzo o di rame furono prodotti in Persia, Mesopotamia, Egitto, nel 12° e 13° sec.; in Giappone, nel 13°-14° sec., si trovano custodie artistiche da s. in lacca dorata e intarsiata di madreperla.
Sin dal 15° sec. lo s. si trova nell’arredamento sotto forma di mobile e di elemento decorativo fisso. Come mobile il tipo più comune di s. è costituito da una lastra di forma e dimensioni variabili, incorniciata e sospesa a parete. Un tipo particolare è lo s. veneziano, racchiuso in una cornice della stessa materia, ricca di motivi decorativi, talora con disegni incisi o dipinti sulla lastra. Si trova anche inserito nei tavoli da toeletta, nelle psiche, nell’armadio a s. (vis-à-vis), e simili. Di rilievo l’impiego dello s. nell’architettura d’interni, come elemento di amplificazione dello spazio e della luce (Versailles; casa di Soane a Londra; castello di Herreninsel sul Chiemsee; oltre a numerosissimi esempi di arredo moderno).
Nell’iconografia lo s. è attributo consueto di virtù, come la Prudenza, oppure di vizi come la Lussuria, e compare frequentemente nelle raffigurazioni di Venere; è impiegato inoltre nelle rappresentazioni allegoriche della Vista o per esprimere concetti come Verità o Vanitas. Come s. magico può essere attributo delle Sibille.
Fisica
In ottica, lo s. (s. ottico) è il più semplice sistema catottrico, costituito da una sola superficie riflettente, piana (s. piani), o curva (s. sferici, paraboloidici, ellissoidici, cilindrici ecc.). Tale superficie è quella che separa due mezzi otticamente diversi; generalmente è la superficie di una lastra di vetro sulla quale vengono realizzate, mediante la deposizione di uno strato metallico, le condizioni per una riflessione (➔) metallica, e dunque con alto e uniforme coefficiente di riflessione.
La formazione dell’immagine
La formazione delle immagini è governata dalle due leggi della riflessione regolare, secondo le quali, nel linguaggio dell’ottica geometrica, raggio incidente e raggio riflesso sono complanari con la normale nel punto d’incidenza e formano con questa angoli uguali.
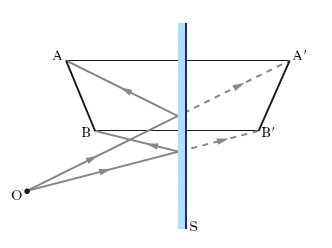
Di un oggetto AB uno s. piano S fornisce un’immagine A′B′ virtuale, diritta, ribaltata, di uguale grandezza (immagine speculare), priva di aberrazioni (fig. 1); un osservatore posto in O ha l’impressione di vedere l’oggetto dietro lo s.; in effetti, l’immagine, dai cui punti sembra che provengano i raggi riflessi, è simmetrica dell’oggetto rispetto alla superficie riflettente.
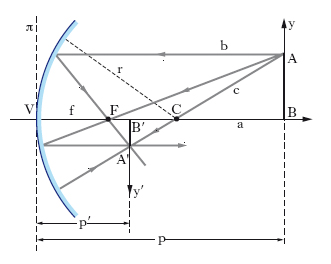
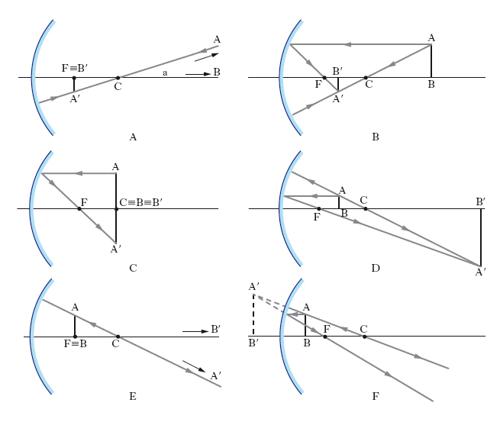
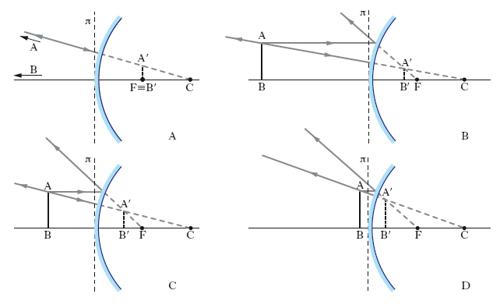
Negli s. sferici concavi la superficie riflettente è la parte concava di una calotta sferica. La teoria della formazione delle immagini è relativamente semplice se si resta entro i limiti delle approssimazioni di Gauss dell’ottica geometrica, e cioè se si considerano raggi parassiali, vale a dire raggi poco inclinati sulla congiungente il vertice V (fig. 2) con il centro C, che ha il nome di asse (principale) dello s., e s. di piccola apertura, vale a dire calotte di dimensioni sensibilmente minori del raggio di curvatura r: entro questi limiti, uno s. sferico concavo è un sistema centrato ortoscopico, che dà cioè immagini prive di aberrazioni. Di questo sistema, i due punti principali coincidono in uno solo, che è il vertice V, e così i due fuochi, che coincidono in un solo fuoco F reale, punto di concorso dei raggi riflessi corrispondenti a un fascio di raggi incidenti paralleli fra loro e all’asse VC, posto su quest’ultimo a una distanza f (distanza focale) da V pari a metà del raggio r della calotta; i due punti nodali coincidono in uno solo, che cade nel centro C. Questa essendo la posizione dei punti cardinali, immediata è la costruzione dell’immagine A′B′ di un oggetto AB: per ogni punto, come mostrato in fig. 2 per il punto A, basterà, per es., considerare il raggio b parallelo all’asse a, che si riflette passando per il fuoco, e il raggio c per il centro, che si riflette su se stesso, il punto d’incontro di tali raggi (o dei loro prolungamenti, nel caso di immagini virtuali) essendo l’immagine o, se si preferisce, il punto coniugato A′ del punto oggetto A. Nella fig. 3 sono schematizzati, in base a questo criterio grafico, alcuni casi particolari che si hanno quando si immagina che un oggetto AB venga progressivamente avvicinato allo specchio. Come si vede, quando l’oggetto è all’infinito (fig. 3 A), l’immagine è reale, capovolta, impiccolita e cade nel piano focale (piano per il fuoco F, ortogonale all’asse a); avvicinandosi l’oggetto al centro C (fig. 3 B), l’immagine, sempre reale e capovolta, procede dal fuoco verso il centro, aumentando di dimensioni, ma mantenendosi sempre impiccolita; quando l’oggetto è nel piano centrale (fig. 3 C), anche l’immagine, reale e capovolta, cade nel piano centrale ed è di uguale grandezza rispetto all’oggetto; procedendo quest’ultimo fra il piano centrale e quello focale (fig. 3 D), l’immagine, ancora reale e capovolta, si forma, ingrandita, al di là del piano centrale; quando l’oggetto è nel piano focale (fig. 3 E), l’immagine, reale, capovolta, infinitamente grande, si forma all’infinito; avvicinandosi ulteriormente l’oggetto allo s., tra il piano focale e la superficie riflettente (fig. 3 F), l’immagine cambia natura, e precisamente diventa virtuale, diritta, ingrandita, e si forma al di là del vertice, cioè dietro lo specchio. Questi risultati, ottenuti per via geometrica, si ritrovano tutti per via analitica mediante la seguente relazione, ricavata, nei limiti delle approssimazioni di Gauss, dalle leggi della riflessione regolare e nota come formula degli s. sferici di piccola apertura:
[1] formula
p, p′ sono le distanze dei punti oggetto e dei punti immagine, rispettivamente, dal piano principale π (fig. 2), cioè dal piano per il vertice, ortogonale all’asse, riferite a un asse di distanze coincidente in direzione con l’asse a, avente l’origine nel vertice V e orientato come indicato, cioè con la parte positiva nello spazio anteriore allo specchio. Poiché a questo asse vanno riferiti anche il raggio r e la distanza focale f, risulta dunque che queste due ultime grandezze, come pure p, sono in ogni caso positive, mentre p′ può risultare, in conseguenza dell’essere p maggiore oppure minore di f, positiva oppure negativa; naturalmente, al fatto che p′ risulti negativa, corrisponde il formarsi dell’immagine al di là dello s., cioè corrisponde un’immagine virtuale. Ulteriori caratteristiche dell’immagine possono ottenersi introducendo l’ingrandimento lineare (trasversale) dello s., cioè il rapporto G tra dimensioni corrispondenti dell’immagine e dell’oggetto, valutate trasversalmente all’asse ottico, con riferimento, per l’oggetto e per l’immagine, ai due assi y, y′ indicati nella fig. 2; si ha:
[2] formula
così, a immagini reali, capovolte, corrisponde un ingrandimento positivo. Se uno s. dà immagini reali, queste possono essere, oltre che osservate a occhio ponendosi sul cammino dei raggi riflessi, anche raccolte su uno schermo d’osservazione o su una lastra fotografica, cosa che invece non può ottenersi con immagini virtuali.
Negli s. sferici convessi la superficie riflettente è la parte convessa di una calotta sferica. Valgono tutte le considerazioni svolte per gli s. concavi; in particolare, nelle approssimazioni di Gauss, cioè per raggi parassiali e s. di piccola apertura, valgono le [1], [2]: si osservi peraltro che stavolta il raggio r (e quindi anche la distanza focale f) è una grandezza negativa, in conseguenza del fatto che il centro (e il fuoco) è virtuale, cioè cade dietro lo specchio. Come senza difficoltà si riconosce in base alle relazioni ora ricordate oppure procedendo per via geometrica (fig. 4), le immagini fornite da uno s. convesso sono sempre virtuali, diritte, impiccolite; via via che l’oggetto, partendo da una posizione infinitamente distante, s’avvicina allo s. sino a portarsi, al limite, nel vertice, l’immagine si sposta dal piano focale verso il piano principale π, aumentando via via di dimensioni, sino a coincidere, nella posizione limite su π, con l’oggetto.
Nella fisica dei plasmi, lo s. magnetico è un dispositivo atto a confinare un gas ionizzato in una regione limitata dello spazio per mezzo di intensi campi magnetici.
Medicina
S. frontale Strumento usato in medicina, specialmente in otorinolaringoiatria, per l’esame di alcune cavità esterne (bocca, fosse nasali, condotto uditivo esterno): consiste in uno specchietto concavo, forato al centro, fissato alla fronte dell’osservatore, e disposto davanti a un suo occhio associato a una sorgente luminosa.
Psicologia
In psicanalisi, fase (o stadio) dello s., fase dello sviluppo infantile compresa fra i 6 e i 18 mesi, la quale costituirebbe la base della progressiva conquista dell’identità del soggetto: il bambino anticipa la padronanza della propria unità corporea identificandosi con la propria immagine allo s., percepita come l’ego ideale.
Trasporti
Specchietti di cortesia S. di piccole dimensioni presenti nelle autovetture (applicati sul retro di una delle due alette parasole, per uso della persona che siede accanto al guidatore).
Specchietti retrovisivi (o retrovisori) S. applicati sia all’esterno degli autoveicoli, su entrambi i lati, orientabili anche elettricamente, sia all’interno, al centro del parabrezza, per consentire al guidatore di rendersi conto di quanto avviene dietro il proprio veicolo e lateralmente; nei motoveicoli gli specchietti retrovisori sono applicati su entrambi i lati del manubrio.