rotismo
(o ruotismo) Sistema di ruote dentate (cilindriche o coniche, a denti diritti o elicoidali) ingranate fra loro in modo che il movimento di una provochi un movimento per ciascuna delle altre. Un r. si dice ordinario se gli assi geometrici delle ruote sono fissi, epicicloidale (o planetario) se gli assi di una o più ruote sono mobili.
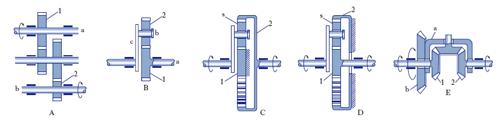
Un r. ordinario cilindrico (fig. A) si compone di tre o più alberi, dei quali i due estremi a e b portano calettata una sola ruota dentata: di queste due ruote estreme l’una (1) è motrice o conduttrice, l’altra (2) è mossa o condotta. Gli alberi intermedi portano invece ciascuno due ruote, una che riceve il movimento dall’albero precedente, l’altra che lo trasmette al seguente. I r. ordinari sono meccanismi a un grado di libertà, quindi a una velocità della conduttrice corrisponde una ben determinata velocità per ciascuna delle altre ruote. Se la velocità angolare delle successive ruote, da quella motrice a quella condotta, diminuisce, il r. si dice riduttore; se aumenta, moltiplicatore. Si definisce rapporto di trasmissione τ del r. il rapporto fra la velocità angolare della ruota condotta e quella della ruota motrice; nei r. moltiplicatori, τ è maggiore di 1 e prende anche il nome di rapporto di moltiplica; nei r. riduttori è minore di 1 e si chiama rapporto di riduzione. Il rapporto di trasmissione per due ruote dentate è uguale all’inverso del rapporto del loro numero di denti; se il r. comprende più coppie di ruote in presa, il suo rapporto di trasmissione è dato dal prodotto dei rapporti di trasmissione delle successive coppie di ruote in presa. A ogni accoppiamento tra due ruote il verso di rotazione si inverte se trattasi di ruote esterne, rimane invariato se trattasi di ruote interne. Il rendimento meccanico del r. è uguale al prodotto dei rendimenti meccanici delle successive coppie. In assenza di perdite per attrito, la potenza disponibile alla ruota condotta è uguale a quella applicata alla ruota motrice e, in tal caso, il momento M della coppia applicata alla ruota motrice (coppia motrice) è uguale al prodotto del rapporto di trasmissione per il momento Mr della coppia applicata alla ruota condotta (coppia resistente): Mr risulta maggiore o minore di M a seconda che il r. è riduttore o moltiplicatore. Quando uno degli alberi intermedi del r. porta una sola ruota, questa si dice oziosa in quanto non influisce sul rapporto di trasmissione, ma unicamente sul senso di rotazione.
Fra i r. epicicloidali, il r. epicicloidale semplice è formato (fig. B) dalla ruota dentata 1 (planetaria) con asse di rotazione a fisso e da un’altra (satellite, 2) con asse di rotazione b mobile intorno ad a, trascinato dal portatreno (o ponte, o leva) c. Un altro tipo di r. epicicloidale è caratterizzato da due ruote planetarie (1 e 2 nelle fig. C e D) con assi fissi coincidenti con quello del portatreno, mentre l’asse del satellite s (o dei satelliti) ruota intorno a quello delle ruote planetarie. Nella fig. C la ruota planetaria 1 è fissa, la 2 è girevole, e il satellite s ingrana con ambedue; nella fig. D la ruota 2 è fissa e la 1 girevole. I r. epicicloidali hanno di norma 2 gradi di libertà, per cui, per descriverne il moto, occorre dare 2 velocità tra le 3 seguenti: velocità n1 della prima ruota planetaria, velocità n2 della seconda ruota planetaria (o del satellite con riguardo al r. semplice), velocità n del portatreno. Dei 3 membri menzionati 2 ricevono dall’esterno azioni motrici e il terzo azioni resistenti o viceversa, in tutte le combinazioni possibili. Molto spesso il r. viene ridotto a un grado di libertà, in quanto la velocità angolare di una ruota planetaria è posta uguale a zero (porre uguale a zero la velocità del portatreno equivale a rendere ordinario il r.). Un r. epicicloidale a ruote coniche è quello impiegato nel differenziale delle automobili (fig. E). Nel suo funzionamento normale il portatreno a è l’elemento motore trascinato in rotazione dalla corona dentata b, mentre alle due ruote planetarie 1 e 2 sono applicati i momenti resistenti; si hanno due gradi di libertà e infatti la velocità di ciascuna delle ruote planetarie può variare in funzione della lunghezza della traiettoria percorsa dalla corrispondente ruota in modo che la velocità del portatreno sia la media delle due. Anche in questo r. si può avere una ruota fissa e un solo grado di libertà.