pressoflessione

fig. 1

fig. 2

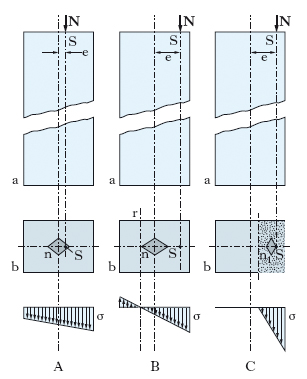
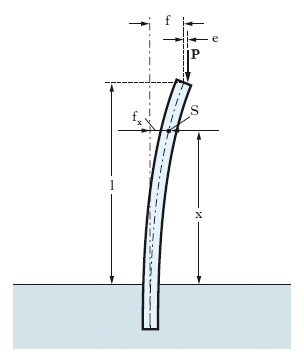
Nella scienza delle costruzioni, sollecitazione composta risultante dalle due sollecitazioni semplici di pressione e di flessione. Nei casi concreti si verifica nelle travi e nei pilastri soggetti a sforzo normale eccentrico (quando lo sforzo normale è di trazione la trave si dice soggetta a tensoflessione). L’insieme delle forze che agiscono sulla generica sezione trasversale b (fig. 1), di un pilastro a è riducibile a un’unica forza N di compressione normale al piano della sezione, ma applicata in un punto S (centro di pressione) diverso dal baricentro della sezione stessa: detta e l’eccentricità del centro di pressione, cioè la distanza della retta di applicazione dal baricentro, la sezione resta soggetta a uno sforzo normale assiale N e a un momento flettente M=Ne (trascurando l’effetto dovuto alla deformazione della struttura, ciò che può essere fatto se questa è ‘corta’). Per il principio di sovrapposizione degli effetti, la tensione normale σ in corrispondenza al generico elemento riesce pari alla somma dei contributi dovuti alla pressione e alla flessione, cioè si ha: σ=N/A+My/I, dove A è l’area della sezione, y è la distanza dell’elemento della sezione dall’asse neutro (➔ flessione), I è il momento d’inerzia della sezione rispetto all’asse neutro medesimo. Per quanto riguarda la tensione normale provocata dalla flessione, è da osservare che l’espressione scritta presuppone che il centro di sollecitazione appartenga a uno degli assi principali d’inerzia della sezione. Diversamente si dovrebbe aggiungere un altro termine a secondo membro per tener conto dei due componenti del momento flettente nei due piani corrispondenti agli assi principali d’inerzia della sezione. In ogni caso l’espressione della σ fornisce una legge di distribuzione lineare. La σ risulta nulla in corrispondenza di ∞¹ punti della sezione allineati su una medesima retta (asse neutro nella p.), non passante per il baricentro, ma parallela all’asse neutro che competerebbe alla flessione semplice. Tale retta risulta l’antipolare del centro di sollecitazione rispetto all’ellisse d’inerzia della sezione considerata. Se il centro di sollecitazione è interno al nocciolo centrale n (fig. 1A) della sezione, l’asse neutro è esterno alla sezione, e questa è pertanto soggetta solo a tensioni normali σ di compressione. Se il centro di sollecitazione è invece esterno al nocciolo (fig. 1B), l’asse neutro r taglia la sezione, e questa risulta perciò soggetta a tensioni σ sia di compressione sia di trazione. Interessante e frequente nella pratica è il caso dei materiali non resistenti (totalmente o parzialmente) a trazione. Se si schematizza la scarsa resistenza a trazione in una totale incapacità di reagire a trazione (questo è lo schema ordinariamente assunto per tutte le murature, comprese quelle in calcestruzzo non armato), ogni qualvolta il centro di sollecitazione è esterno al nocciolo centrale della sezione si generano tensioni normali che portano alla fessurazione, cioè alla rottura delle fibre resistenti nella parte della trave soggetta a sforzi di trazione. Di conseguenza la sezione generica b (fig. 1C) della trave a si parzializza (➔ parzializzazione), cioè riduce la sua parte effettivamente reagente, con sollecitazione di compressione σ, fino a che tale parte (punteggiata in fig. 1C) viene a contenere il centro di sollecitazione S sul perimetro del suo nocciolo centrale di inerzia n₁. In ogni caso è necessario per l’equilibrio che il centro di sollecitazione cada all’interno della sezione primitiva. P. e carico di punta Nel caso dei solidi snelli, cioè di lunghezza notevole rispetto alle dimensioni della sezione trasversale, la sollecitazione di p. non può essere ridotta alla semplice sovrapposizione degli effetti di una pressione semplice e di un momento flettente, perché, risultando non trascurabili le ordinate della deformazione di flessione, ne riesce incrementata l’eccentricità dello sforzo normale e il momento flettente diviene perciò funzione dell’ordinata di deformazione. Ci si riferisca, per es. (fig. 2), a un solido verticale di lunghezza l incastrato al piede e soggetto in sommità a un carico eccentrico P; l’eccentricità e del carico provoca l’inflessione del solido e quindi il momento flettente in un punto generico S è: M_x=P (e+f−f_x), essendo f la freccia in sommità. Se si scrive l’equazione differenziale della linea elastica, EIf″_x=−M_x, e si integra, si ottiene il valore della f_x in funzione di x e il valore della f in sommità:

dove E è il modulo di elasticità longitudinale, I il momento d’inerzia della sezione rispetto all’asse baricentrale normale al piano di sollecitazione. Questa formula mostra che la freccia cresce con il carico assai più che linearmente. Anzi, il valore di f tende all’infinito (cioè non esiste più una configurazione equilibrata della mensola) per

[1] formula

che è la nota formula del carico critico, dovuta a Eulero. In tal caso il sistema perde stabilità per qualunque valore dell’eccentricità e. In particolare il fenomeno si verificherebbe anche se il carico fosse perfettamente centrato (carico di punta), perché in questo caso la trave ammette anche una configurazione di equilibrio (quella rettilinea), ma si tratta di una configurazione di equilibrio elastico instabile (➔ stabilità). Il pericolo del fenomeno di instabilità è tanto maggiore quanto maggiore è il rapporto l/ρ_min (grado di snellezza) per la trave soggetta a carico di punta (con ρ_min minimo raggio d’inerzia della sezione trasversale). Invece per piccoli valori di questo rapporto (cioè per le travi corte) il valore del carico critico fornito dalla [1] diviene maggiore del carico limite che la trave può sopportare per la sua resistenza a schiacciamento, e ciò perché nella determinazione del carico critico si è ritenuta valida la legge di Hooke, mentre essa perde la sua validità per solidi corti sollecitati oltre il limite di proporzionalità. Nel caso di travi o pilastri vincolati diversamente il carico critico di Eulero assume valori diversi da quello suddetto. La tensione critica si ottiene ovviamente dividendo il carico critico per l’area A della sezione: σ_cr=P_cr/A; quanto alla tensione di sicurezza, essa si ottiene dividendo la tensione critica per un opportuno coefficiente di sicurezza che viene generalmente assunto tanto più grande quanto maggiore è la snellezza della struttura presa in considerazione.